σ迁移反应
σ迁移反应(Sigmatropic reaction)是反应物一个σ键沿着共轭体系从一个位置转移到另一个位置的一类周环反应。[1]通常反应是分子内的,同时伴随有π键的转移,但底物总的π键和σ键数保持不变。一般情况下σ迁移反应不需催化剂,但少数反应会受到路易斯酸的催化。
σ迁移反应符合分子轨道对称守恒原理,是协同反应的一种,也就是说原有σ键的断裂,新σ键的生成,以及π键的转移都是经过环状过渡态协同一步完成的。以Cope重排反应为例:
![[3,3]sigma重排](http://upload.wikimedia.org/wikipedia/commons/thumb/7/7e/-3%2C3-SigmatropicRearrangement%27.png/425px--3%2C3-SigmatropicRearrangement%27.png)
命名
[编辑]σ迁移反应的命名方法,是先将迁移前的σ键的两个原子均定为1号,从其两端分别开始编号,把新生成的σ键所连接的两个原子的编号i、j放在方括号内,记为迁移。习惯上。因此,上面图示的反应是一个迁移反应。也可以将迁移的取代基原子写在前面,写成诸如迁移反应的形式。
迁移后,如果新形成的σ键在π体系的同侧,称之为同面迁移;反之,则称为异面迁移。图示 (页面存档备份,存于互联网档案馆)它们也可以写在标记中,同面以s表示,异面以a表示。下面的迁移反应对于氢原子和戊二烯基来说都是同面的,因此是一个迁移反应。

在迁移反应中,如果和迁移键相连的碳原子为手性碳,而且迁移后,该碳原子仍在键断裂处形成新键,称为构型保持;如果新键在原键断裂处的相反位置形成,则称为构型翻转。同芳香性可以在标记中用homo表示。
机理
[编辑]以为例。根据前线轨道理论,假定反应中发生迁移的σ键首先发生均裂,生成一个氢原子(或碳自由基)和一个奇数碳的共轭体系自由基,而反应的实质是氢原子(或碳自由基)在奇数碳的共轭体系自由基上发生的迁移。一般认为,反应中真正涉及到的是奇数碳共轭体系中含有单电子的前线轨道,它既是最高占有分子轨道(HOMO),也是最低未占有分子轨道(LUMO),而且反应的立体选择性也完全取决于该前线轨道的对称性。基态时,它是一个非键轨道,具有以下所示的分子轨道示意图,其中的数字与上面命名一节的数字含义吻合。
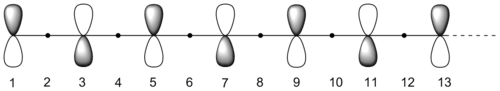
可以看出,该前线轨道中,所有偶数碳上的电子云密度都为零,而奇数碳上的电子云密度数值相等,波相交替变化。奇数碳又分为两种,一种为4n+1类型,另一种为4n-1类型;前者前线轨道具有镜面对称性,而后者具有镜面反对称性。激发态时,电子发生跃迁,因此这两种类型的镜面对称性发生转换,前者具镜面反对称性,后者具镜面对称性。
由于σ迁移反应是符合分子轨道对称守恒原理的反应,因此形成新的σ键时,必须发生的是同位相的重叠。以迁移为例,若它属于4n+1类型,则为了满足对称性的要求,基态时,单占轨道对镜面对称,只有同面迁移是允许的;激发态时,单占轨道对镜面反对称,只有异面迁移是允许的。对于4n-1类型则正好相反。如果迁移的原子是手性碳原子,那么在进行类型的迁移反应时,4n-1与1号原子的波相相反,因此只有用断键轨道的另一瓣(符号相反)与奇数碳共轭体系发生重叠。自然,新键在断键位置的相反方向形成,手性碳发生构型翻转。
迁移反应也可以用类似的方法来分析。迁移的σ键发生均裂后,形成两个奇数碳共轭体系自由基,σ迁移反应中起决定作用的是它们两个的单占前线轨道。σ迁移反应具有以下选择性规则:[2]
| 参加环型过渡态的π电子数或 | 4n+2 | 4n | |||||
|---|---|---|---|---|---|---|---|
| 反应分类 | |||||||
| 迁移 | 迁移 | 迁移 | |||||
| 构型保持 | 构型翻转 | ||||||
| 同面迁移 | 同面迁移 | 异面迁移 | 同面-同面迁移 异面-异面迁移 |
Δ | hν | Δ | hν |
| 允许 | 禁阻 | 禁阻 | 允许 | ||||
| 异面迁移 | 异面迁移 | 同面迁移 | 同面-异面迁移 | Δ | hν | Δ | hν |
| 禁阻 | 允许 | 允许 | 禁阻 | ||||
| 注:“允许”指“对称性允许”,“禁阻”指“对称性禁阻”。 | |||||||
例子
[编辑]最常见的σ迁移反应有[3,3]σ迁移反应和[2,3]σ迁移反应两种,前者包括Cope重排反应、Claisen重排反应、Carroll重排反应以及Fischer吲哚合成,后者包括Gassman吲哚合成以及一大类含有杂原子迁移的反应。按迁移原子来分,则σ迁移反应常见的两类是“甲基转位”和“负氢转位”反应。
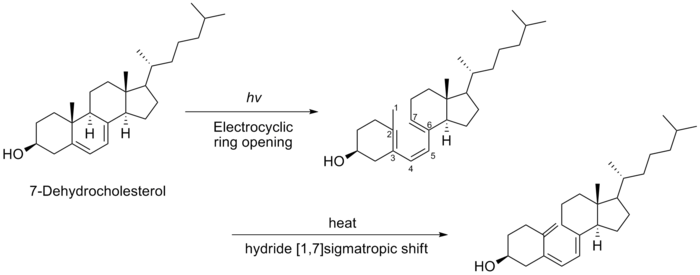
下面图中是维生素D3生物合成的最后几步反应。首先是7-脱氢胆固醇受光照发生逆电环化反应,生成含有1,3,5-己三烯结构的前维生素D3。而后前维生素D3在加热情况下,发生一个迁移反应,得到维生素D3。
参见
[编辑]参考资料
[编辑]- ^ F.A. Carey, R.J. Sundberg, Advanced Organic Chemistry. Part A. ISBN 0-306-41198-9
- ^ 邢其毅、裴伟伟、徐瑞秋、裴坚。《基础有机化学》(第三版)下册。北京:高等教育出版社,2005年12月:736。ISBN 978-7-04-017755-8

![{\displaystyle [i,j]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cebec00b1e1a395bc4c0e5b543c5b7b9fd69a77)
![{\displaystyle [i]\leq [j]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa98b7a76bc2de2ad0acb70fa97f6eb8c194c9d1)
![{\displaystyle [3,3]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73058483d9760f087cee71dbaf23a8664bfee79f)
![{\displaystyle H[1,5]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53a861cc0eca0419fd7c890cf6390f36eb8c25c7)
![{\displaystyle H[1s,5s]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d17f0ddbe795a7bd8c75a95a2e25014cd63a7c7f)
![{\displaystyle C[i,j]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70c964bb462b027487025ff084660eef21b2676f)
![{\displaystyle [1,j]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/410c16211a9e9d7254dad92068e9b21f041bb6be)
![{\displaystyle H[1,j]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/636e9125eb4a0184c5eeea2fa59a318d768c55d4)
![{\displaystyle [1,4n-1]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e994ea8c8127b71517434344093fb61877c6eec)


![{\displaystyle C[1,j]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1a7b48d45342a9de1bf6c0411f75f210932fb67)
![{\displaystyle H[1,7]\sigma \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf446e7d5acc0ef622db8a81ad8f4ff3b07adb3)