力学平衡
外观
(重定向自機械平衡)
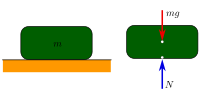
当一个质点、刚体或质点系的速度矢量为常矢量时,就称该物体或系统处于力学平衡(Mechanical equilibrium)或機械平衡状态[1][2][3]。特别地,当一个静止的质点或质点系处于力学平衡状态时,该质点或质点系即处于靜力平衡或靜態平衡状态[4][5]。物体的力学平衡状态在任何和该物体相对静止的参考系中均不变。
当外力对质点系上任何一点所产生的合力矩时,称质点系处于转动平衡状态。
更一般地,根据变分原理,在保守系统中,当位形空间中某势能的泛函(廣義位勢函數)对广义坐标的梯度在某点为零时,系统在该点处于平衡位置[1]。
稳定性
[编辑]


处于力学平衡状态的系统的一个重要性质是稳定性。先考察只有一个广义坐标的系统。该系统处于平衡态时,其势能的泛函对广义坐标的一阶变分为零;根据二阶变分的正负性,平衡状态可进一步分为三类[6]:
- 二阶变分为负:势能处于區域极大值,系统处在不稳定平衡,任何微小扰动都会使系统远离平衡态。
- 二阶变分为正:势能处于區域极小值,系统处在稳定平衡,受到微小扰动而偏离平衡位置时,系统能自动恢复到平衡态。
- 二阶变分为零:势能不变,系统处在随遇平衡,受到微小扰动而偏离平衡位置时,系统在新的位置也能平衡。
如果位势函数在驻点的二阶变分不存在,高阶变分可以此类推。
推广到多维空间情况时,一个系统有可能在某一维度处于稳定平衡,而在另一维度处于不稳定平衡,如鞍点。通常意义下的稳定平衡指该系统在所有维度都处于稳定平衡状态。
例子
[编辑]力学平衡的一个很重要的特例是静力平衡,例如:静置在桌面上的书本就处于静力平衡状态。其中,凸均匀体可以具有的平衡点的最小数目格外吸引研究者关注。在二维空间中,这个最小数目是4(四頂點定理);但在三维空间中存在只有一个稳定平衡点和一个不稳定平衡点的物体(冈布茨)。
沿滑梯匀速下滑的孩子处于力学平衡状态,但不处于静力平衡状态(相对于固定的滑梯和地面参考系)。
参见
[编辑]参考文献
[编辑]- ^ 1.0 1.1 徐燕侯,郭长铭,周凯元. 理论力学 修订版. 中国科学技术大学出版社. 2000: 第11章;第17章. ISBN 7-312-01169-1.
- ^ John L Synge & Byron A Griffith. Principles of Mechanics 2nd. McGraw-Hill. 1949: 45–46.
- ^ Beer FP, Johnston ER, Mazurek DF, Cornell PJ, and Eisenberg, ER. (2009) Vector Mechanics for Engineers: Statics and Dymanics. 9th ed. McGraw-Hill. p 158.
- ^ Herbert Charles Corben & Philip Stehle. Classical Mechanics Reprint of 1960 second. Courier Dover Publications. 1994: 113 [2014-08-13]. ISBN 0-486-68063-0. (原始内容存档于2020-05-01).
- ^ Lakshmana C. Rao, J. Lakshminarasimhan, Raju Sethuraman, Srinivasan M. Sivakumar. Engineering Mechanics. PHI Learning Pvt. Ltd. 2004: 6 [2014-08-13]. ISBN 81-203-2189-8. (原始内容存档于2020-05-01).
- ^ 朱滨. 弹性力学. 中国科学技术大学出版社. 2008: 290. ISBN 978-7-312-02247-0.
延伸阅读
[编辑]- 舒幼生《力学》北京大学出版社 ISBN 978-730-109401-3
- 杨维纮《力学与理论力学》科学出版社 ISBN 978-703-020513-1
- Marion JB and Thornton ST. (1995) Classical Dynamics of Particles and Systems. Fourth Edition, Harcourt Brace & Company.


