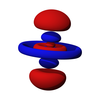
混成軌域
外观
(重定向自雜化軌道)
此條目需要擴充。 (2011年9月21日) |
此條目需要精通或熟悉相关主题的编者参与及协助编辑。 |
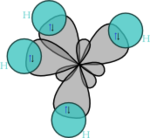
混成軌域(英語:Hybrid orbital)是指原子軌域經混成(hybridization)後所形成的能量简并的新轨道,用以定量描述原子間的鍵結性質。與價層電子對互斥理論可共同用來解釋分子軌域的形狀。混成概念是萊納斯·鮑林於1931年提出。
发展史
[编辑]化学家萊納斯·鮑林第一个提出了杂化轨道理论来解释甲烷(CH4)等分子的结构[1]。 这个概念原本是为了解释简单的化学系统而开发的,但是这种方法后来被广泛应用,至今天它仍然是一种解释有机化合物结构的有效理论。
轨道是描述电子在分子中的行为的一个模型。对于较简单的原子,如氢原子,薛定谔方程可以被精确求解。在较重的原子(如碳、氮、氧)中,原子使用了2s和2p轨道,类似氢原子的激发态轨道,杂化轨道被认为是这些原子轨道以不同的比例互相叠加而成的混合。杂化轨道理论给出了路易士結構的量子力学解释,因而在有机化学里得到了广泛应用。
例子
[编辑]
| 类别 | spx混成 | sdx混成 | spxdy混成 |
|---|---|---|---|
| 主族/ 过渡金属 |
仅过渡金属 | ||
| AX2 | |||
| AX3 |
|
||
| AX4 |
|
| |
| AX6 |
|
| |
| 轨道间角 | |||
| AX5 | 三角雙錐 |
|---|---|

| |
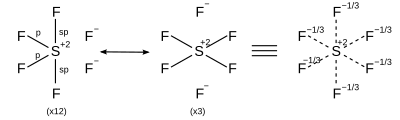
| AX6 | 正八面體 |
| |
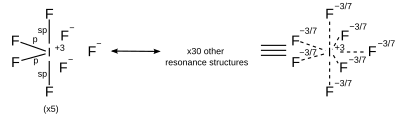
| AX7 | 五角雙錐 |
|
参考文献
[编辑]- ^ Pauling, L., The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules, Journal of the American Chemical Society, 1931, 53 (4): 1367–1400, doi:10.1021/ja01355a027