空间 (数学)
数学上,空间是指一种具有特殊性质及一些额外结构的集合(有时称为全集)。在初等數學或中學數學中,空間通常指三維空間。 现代数学使用了多种类型的空间,如欧几里得空间、线性空间、拓扑空间、希尔伯特空间或概率空间,但并不存在單稱為「空間」的數學物件。[1][a]

空间由被视为点的数学对象和点之间的关系组成。 点的性质可以千差万别:例如,点可以是集合的元素,另一个空间上的函数,也可以是另一个空间的子空间。点之间的关系决定了空间的性质,更确切地说一般认为同构空间完全相同,空间之间的同构是点之间的一一对应关系。例如,欧几里得公理唯一确定了三维欧几里得空间各点之间的关系,[b]所以所有三维欧几里得空间都是相同的。
数学对象应被视为几何“空间”还是代数“结构”,并不总是很清楚。尼古拉·布尔巴基[2]提出了结构的一般定义,包括了所有常见的空间类型,提供了同构的一般证明方法,并证明了同构结构之间的性质转移是合理的。
历史
[编辑]| 古典 | 现代 |
|---|---|
| 公理(axiom)是定义的明显含义 | 公理(axiom)是约定俗成的 |
| 定理(theorem)是绝对客观的真理 | 定理(theorem)是相应公理的含义 |
| 点、线等之间的关系由其性质决定 | 点、线等之间的关系是必要的,而其性质不必要 |
| 数学对象呈现为自身结构 | 数学理论描述了数学对象的性质 |
| 几何对应实验现实 | 几何是数学真理 |
| 空间的所有几何性质都来自公理 | 空间的公理不能决定所有几何性质 |
| 几何是一门独立、自主的学科 | 经典几何是一种通用的数学语言 |
| 空间是三维的 | 不同的维度概念适用于不同类型的空间 |
| 空间是几何的全集 | 空间只是数学结构,出现在数学的各个分支中 |
几何学黄金时代之前
[编辑]
古希腊数学中,“空间”指日常生活中观察到的三维现实的几何抽象。约公元前300年,欧几里得给出了关于空间性质的公理,将所有数学都建立在几何基础上,甚至通过比较线段长度来定义数字。
1637年,勒内·笛卡尔提出了直角坐标系(解析几何)。[3]当时,几何定理被视作可通过直觉和推理实现认识的绝对客观真理,类似于自然科学的对象;[4]:11公理则被认为是定义的明显含义。[4]:15
几何图形有两种等价关系:全等和相似。平移、旋转和翻折对图形进行全等变换,位似变换得到相似图形。例如,所有圆都相似,但椭圆和圆不相似。第三种等价关系由加斯帕尔·蒙日于1795年提出,出现在射影几何中:在适当的投影变换下,椭圆、抛物线和双曲线都会变成圆,称它们射影等价。
欧几里得几何与射影几何之间的关系[4]:133表明,数学对象并非以结构呈现。[4]:21数学对象的性质由数学理论描述,而这些性质作为公理,是理论的基础。[4]:20
距离和角度不会出现在射影几何定理中,因为射影几何公理中没有出现这些概念,也没有从概念中定义出来。“三角形的内角和是多少”这样的问题,在欧几里得几何中有意义,但在射影几何中则毫无意义。
19世纪出现了不同的情况:在某些几何中,三角形内角和定义明确,但异于一般值(180°)。尼古拉·罗巴切夫斯基和鲍耶·亚诺什分别于1829年和1832年(高斯于1816年发现,未发表)[4]:133引入了非欧双曲几何,即内角和取决于具体的三角形,且总小于180°。欧金尼奥·贝尔特拉米(1868)、费利克斯·克莱因(1871)分别获得了非欧双曲几何“模型”,从而完全证明了这理论在逻辑上的可能性。[4]:24[5]
这一发现迫使人们放弃了对欧几里得几何为真理的宣称,表明公理并非“显而易见”,也不是“定义的含义”,而是假设。它们不必匹配实验现实,它的定理也不失为“数学真理”。[4]:15
非欧几何的欧氏模型,是选择欧氏空间中的对象及之间的关系,这些关系满足非欧几何的所有公理(因此也满足所有定理)。这些欧氏对象和关系模仿了非欧关系,这表明在数学中,对象间的关系是必不可少的,而对象的性质却不是。
几何学黄金时代及之后
[编辑]英语中的几何学一词是geometry,来自古希腊语geo-“地”与-metron“测量”,最初指的是测量生活中空间的长度、区域的面积与体积的实用方法,后来得到了推广。
据Bourbaki[4]:131,1795年(蒙日《画法几何学》)到1872年(克莱因《埃尔兰根纲领》)这段时间可以称为“几何学黄金时代”。欧几里得几何最初研究的空间,叫做三维欧几里得空间。欧几里得在23个世纪之前将其公理化,后来得到了希尔伯特公理、塔斯基公理和伯克霍夫公理的重新诠释,它们通过公理约束的原始概念(如“点”“之间”“全等”)来描述空间。
解析几何取得了巨大进步,并成功通过变换群不变式的计算,取代了经典几何定理。[4]:134,5那时起,业余数学家更关心古典几何的新定理。[4]:136但古典几何的遗产并没有丢失。Bourbaki认为[4]:138“古典几何学作为一门独立、活跃学科的角色被超越了,因此它被转化为当代数学的一种通用语言。”
同时,数开始取代集合成为数学的基础。例如,理查德·戴德金的论文《连续性与无理数》(1872)断言直线上的点应具有戴德金分割性质,因此直线与实数集是一回事。戴德金谨慎地指出,这是无法证明的假设。在现代的论述中,这通常被视为线的定义,几何从而简化为算术。三维欧几里得空间被定义为仿射空间,其元素差的相关向量空间具有内积。[6]像欧几里得那样“从头来”的定义现在已不常用,因为没有揭示空间与其他空间的关系。此外,三维射影空间现在被定义为四维向量空间的所有一维子空间(即过原点的直线)的空间。基的转变需要新的公理,如采用这些公理,几何学经典公理就变成了定理。
现在,空间由选定的数学对象(例如,另一个空间上的函数,或另一个空间的子空间,或仅仅是集合的元素)组成,这些对象被视为点,而点之间的关系则是选定的。因此,空间只是一种方便的数学结构。可能会认为与其他数学对象相比,“空间”更具有几何感,但事实并非总是如此。
1854年,伯恩哈德·黎曼在就职演讲上指出,以n个实数为参数的数学对象可当做是n维空间中的点。[4]:140当代数学家仍遵循这一思想,并发现在几乎所有地方使用经典几何术语极具启发性。[4]:138
函数是重要的数学对象,正如黎曼指出,函数一般构成无穷维的函数空间,[4]:141在20世纪的泛函分析中得到了详细阐述。
空间的分类
[编辑]3个分类层级
[编辑]每种空间虽然都有自己的定义,但“空间”的一般概念却无法形式化。有些结构可叫做“空间”,有些则不能,没有明确标准。另外,“结构”也没有能通行的定义。据Pudlák所说[7]:“数学[……]不能完全用数学结构这样的单一概念来解释。然而,布尔巴基的结构主义方法是我们所拥有的最好的方法。”布尔巴基的结构主义方法将在#空间与结构中讨论,现在先按他的精神,概述空间(和结构)的可能分类。
我们将空间分为3层。鉴于每种数学理论都由属性描述对象,那么首先就要问:具体是哪些属性?这是第1层(顶层)。第2层要考虑解答特别重要(在第1层有意义)的问题。在第三级分类中,则考虑所有可能问题。
例如,欧几里得空间和射影空间的区别属于一级分类的区别,因为两点之间的距离在欧几里得空间中是确定的,而在投影空间中是不确定的。“三角形内角和是多少”在欧几里得空间中有意义,但在射影空间中无意义;在非欧空间中,这个问题也有意义,而异于欧氏空间,后者的区别便不属于一级。欧几里得平面与欧几里得三维空间之间的区别也不是一级分类的区别:“维度具体是多少”的问题,在两种情形下都有意义。
二级分类可以区分欧氏空间和非欧空间、有限维空间和无限维空间、紧空间和非紧空间等。用布尔巴基的话说,[2]二级分类是按“种”分类,不过与生物分类不同,一个空间可能属于多个“种”。
三级分类区分不同维度的空间,但不区分欧几里得平面和所有实数对的集合(都是二维欧氏空间)。更正式地说,三级分类的标准是同构。空间之间的同构定义为两者的点之间的一一对应,保留了一级分类规定的所有关系。同构就是空间之间的等价关系。
同构的概念揭示了一级分类。给定同一一级分类的两个空间之间的一一对应关系,便可以问这是否是同构。这个问题对于两个不同类的空间毫无意义。
与自身同构,称为自同构。欧氏空间的自同构是平移、旋转、反射和它们的组合。同维欧氏空间都是同质的,因为每个点都可以通过自同构变换成其他每个点。
欧几里得公理[b]没留下自由的空间,唯一决定了空间的所有几何属性。更确切地说,所有三维欧氏空间都互相同构。用Bourbaki的话来说,相应的理论是唯一等价(“单价”)的。相对地,拓扑空间之间通常不同构,理论是“多价的”。类似想法也见于数理逻辑:范畴理论的所有同势模型都相互同构。Bourbaki[8]认为,对多价理论的研究是现代数学区别于古典数学的显著特征。
空间种类之间的关系
[编辑]拓扑概念(连续、收敛、开集、闭集等等)在欧氏空间中有自然的定义,也就是说欧氏空间都是拓扑空间。两个欧氏空间之间的同构也是相应拓扑空间的同构(同胚),但反过来就不是了:同胚可能会使距离改变。用布尔巴基的话说[2],“拓扑空间”是“欧氏空间”结构的内在结构。类似观点见于范畴论:欧氏空间范畴是拓扑空间范畴上的具体范畴;遗忘函子将前者映射到后者。
3维欧氏空间是欧氏空间的特例。用布尔巴基的话说,[2]3维欧氏空间“种”要比欧氏空间“种”更丰富。同样,紧拓扑空间的种类也比拓扑空间的种类丰富。
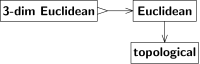
如图3所示,空间种类的此种关系可用图表示。A到B的箭头意味着,A空间也是B空间;或可视作B空间;或提供了B空间,等等。将A和B视作空间种类,可以将箭头解释为A到B的转化(用Bourbaki的话说[9]“从A空间到B空间的推导过程”。除非A、B是集合类,否则不完全是函数;这一细微差别不会影响下面的讨论)。图3的两个箭头都不可逆,但原因不同。
“欧几里得”到“拓扑”的过程是遗忘的。拓扑区分连续与不连续,但不分直线和曲线。直觉告诉我们,欧几里得结构无法从拓扑中复原。可以证明拓扑空间的自同构(即自同胚)不同于欧几里得空间的自同构(即不是平移、旋转和反射的组合)。这样的变换会改变(不过仍然同构)给定的欧氏结构,而前后的欧氏结构都对应单一拓扑结构。
相比之下,从“3维欧氏”到“欧氏”空间的变换就不是遗忘的;后者不一定是3维的,但若恰好是3维的,则不会丢失任何结构。后一种变换是单射(一到一),而前一种变换不是(多到一)。我们用尾部带钩的箭头“↣”表示单射。
两种变换都不是满射,即并非每个B空间都来自A空间。首先,3维欧氏空间是欧氏空间的特例而非通例;其次,欧氏空间的拓扑是拓扑的特例(例如,必须是非紧连通的,等等)。记满射为双头箭头“↠”,例子见图4;其中“实线性拓扑”到“实线性”的箭头是双头的,因为每个实线性空间都有一些(至少一个)与线性结构兼容的拓扑。
这种拓扑一般来说不唯一,但当实线性空间为有限维时唯一。对这些空间而言,变换既是单射也是双射,即双射;如图4中“有限维实线性拓扑”到“有限维实线性”的箭头;逆变换也存在(表示为反向箭头)。因此,这两种结构等价。在实践中,一般不区分等价的结构种类。[10]等价结构可被视为单一结构,如图4的大框所示。
箭头表示的变换服从同构,也就是说两个同构A空间会产生两个同构B空间。
图4上的图是交换图:图中同始同终的有向路径都会导向相同的结果。除了图9中的虚线箭头外,下面的其他图也是交换图。“拓扑”到“可测”的箭头是虚线,原因是:“为将拓扑空间转为可测空间,需要赋予一个σ代数。最常用的是博雷尔集的σ代数,也有其他选择。”实箭头表示平凡的所谓“典型”变换,自然而然地提出并广泛使用。例如,在欧氏空间上讨论连续函数时,无需说明其拓扑结构。事实上存在其他拓扑结构,如细拓扑;但这些拓扑结构总是明确指定的,因为它们远不如常用的拓扑结构引人注目。虚线箭头表示有几种拓扑结构在使用,但没有一种很普遍。
空间类型
[编辑]线性空间与拓扑空间
[编辑]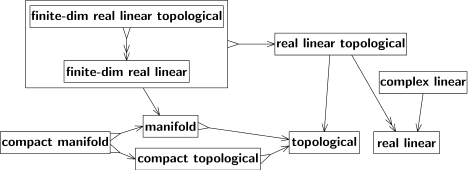
线性空间具有代数性质,有实线性空间(实数域上)、复线性空间(复数域上),以及更一般的任意域上的线性空间。复线性空间也是实线性空间(后者是前者的基),例如一维复线性空间的复平面可以同构变换为二维实线性空间;实线则只能被视作一维实线性空间。更一般地说,域上的向量空间也具有子域上的向量空间的结构。
根据定义,线性空间中的线性运算产生了直线(及平面等线性子空间)、平行线、椭圆(及椭球)等概念。但是无法定义正交(垂直),也找不到圆,因为线性空间中没有标量积那样的结构来测量角度。线性空间的维度是线性独立向量的最大数目,也等价于跨空间的向量的最小数目;这个数可能是无限的。同一域上的两个线性空间只有在维度相同时才同构;n维复线性空间也是2n维实线性空间。
拓扑空间具有分析性质。根据其定义,拓扑空间中的开集可引出连续函数、路径、映射;收敛数列、极限;内部、边界、外部等概念。而一致连续、有界集、柯西序列、可微函数(路径、映射)则仍未定义。拓扑空间之间的同构叫做同胚,它们是两个方向上连续的一一对应关系。开区间(0,1)与整条数线(−∞,∞)同胚,但与闭区间[0,1]、与圆则不同胚。正方体表面与球面同胚,但不与环面同胚。不同维度的欧氏空间不同胚,这一点似乎显而易见,却不易证明。拓扑空间的维度也难以定义,有归纳维数(图形的边界维度通常比图形维度小1的归纳)和拓扑维数等。对n维欧氏空间,两者都等于n。
拓扑空间的子集仍是拓扑空间(相对地,线性空间只有线性子集仍是线性空间)。点集拓扑学研究的任意拓扑空间种类繁多,无法进行基于同胚的完整分类。紧拓扑空间是一种重要的拓扑空间(此类中的一种),其上的连续函数都有界。闭区间[0,1]与扩展实数线[−∞,∞]都是紧空间;开区间(0,1)和数线(−∞,∞)则不是。几何拓扑学研究流形(此类中的另一种),它们与欧氏空间局部同胚(并满足一些额外条件)。低维流形在同胚意义上有完全的分类。
线性结构和拓扑结构都蕴含于拓扑向量空间(或拓扑线性空间)结构。线性拓扑空间是具有连续线性运算的拓扑空间,因此,同样是拓扑的线性空间一般不是线性拓扑空间。
有限维线性空间都是线性拓扑空间,因为其中只有一种拓扑结构,使其成为线性拓扑空间。因此“有限维线性空间”与“有限维线性拓扑空间”等价,所以有限维线性拓扑空间的可逆线性变换都是同胚变换。对有限维实线性空间,这三个维度概念(1个代数维度与2个拓扑维度)是一致的;但在无限维空间中,不同拓扑结构可以符合给定的线性结构,可逆线性变换一般不是同胚变换。
仿射与射影空间
[编辑]
通过线性空间引入仿射空间和射影空间 是很方便的,具体如下。n+1维线性空间的n维线性子空间与原空间不同类,包含一个特殊点:原点。用外部向量移动它,就得到n维仿射子空间,这是同累变换。仿射空间不必包含于线性空间中,但与某线性空间的仿射子空间同构。给定域上的所有n维仿射空间都互相同构,用约翰·拜艾兹的话说:“仿射空间是忘记了原点的向量空间。”特别地,线性空间都是仿射空间。
给定n+1维线性空间L中的n维仿射子空间A,A中直线可定义为A与L的二维线性子空间(不与A平行的过原点平面)的交。更一般地说,A的k维仿射子空间是A与同A相交的L的k+1维线性子空间的交。
仿射子空间A的每点都是A与L的一维线性子空间的交点。但L的一部分一维子空间与A平行,可以说它们相交于无穷远。根据定义,(n+1)维线性空间的所有一维线性子空间的集合,是n维射影空间;仿射子空间A则作为合适子集,嵌入在射影空间中。但射影空间本身是同类的。射影空间中的直线对应(n+1)维线性空间的2维线性子空间;更一般地说,射影空间的k维射影子空间对应(n+1)维线性空间的(k+1)维线性子空间,且与k维射影空间同构。
这样,仿射空间和射影空间具有代数性质;它们可以是实空间、复空间,可以是任何域上的空间。
实或复仿射空间或射影空间也是拓扑空间。仿射空间是非紧流形,而射影空间是紧流形。在实射影空间中,直线与圆同胚,因此是紧的,这与仿射空间线性中的直线不同。
度量空间与一致空间
[编辑]
度量空间定义了点之间的距离。度量空间之间的同构称为等距(isometry)。度量空间是拓扑空间;若拓扑空间可蕴含于度量空间,称拓扑空间可度量。所有流形都可度量。
度量空间中,可以定义闭集和柯西序列。称所有柯西序列收敛的度量空间为完备空间。不完备空间都作为稠密集,嵌入到某个完备空间中;紧度量空间都是完备空间;数线是非紧完备空间;开区间(0,1)不完备。
欧氏空间都是完备空间。此外,欧氏空间的所有几何概念都可用度量描述。例如,连接两定点A、C的直线段由所有点B组成,这样|AC|等于|AB|+|BC|。
豪斯多夫维数(与覆盖给定集的小球数有关)适用于度量空间,可以不是整数(如分形)。n维欧氏空间的豪斯多夫维数都是n。
一致空间没有距离,但仍允许均匀连续与柯西序列(或柯西滤子或柯西网)、紧与完备。一致空间都是拓扑空间;线性拓扑空间(无论可否度量)也是一致空间,在有限维时完备,在无限维时通常不完备。更一般地说,交换拓扑群都是一致空间。非交换拓扑群则蕴含左不变、右不变两个一致结构。
赋范空间、巴拿赫空间、内积空间与希尔伯特空间
[编辑]
欧氏空间中的向量构成线性空间,但每个向量x都有长度,即范数。具有范数的实或复线性空间就是赋范空间。赋范空间既是线性拓扑空间,又是度量空间。巴拿赫空间是完备赋范空间,许多序列或函数的空间都是无穷维巴拿赫空间。 范数<1的所有向量之集构成赋范空间的单位球,是凸的中心对称集,一般不是椭球,可能是多边形(平面上),或更一般地是多面体(在任意有限维上)。平行四边形法则
在赋范空间中通常不适用,但在欧氏空间中对向量成立,因为向量的欧氏平方范数是它与自身的内积:.
内积空间是实或复线性空间,具有双线性或半双线性形式,满足某些条件,称为内积。内积空间都是赋范空间。当且仅当赋范空间满足平行四边形法则,或其单位球是椭球时,它才蕴含于内积空间。内积空间定义了向量夹角。 希尔伯特空间是完备内积空间(有人坚称其必须是复空间,另一些人也承认实希尔伯特空间) 。许多序列或函数的空间都是无穷维希尔伯特空间。希尔伯特空间在量子力学中非常重要。[11] n维线性实内积空间都互相同构。可以说,n维欧氏空间就是无原点的n维实内积空间。
光滑流形与黎曼流形
[编辑]
光滑流形不叫做“空间”但可以是。光滑流形都是拓扑流形,可以嵌入有限维线性空间。有限维线性空间中的光滑面是光滑流形:例如,椭球面是光滑流形,而多面体表面则不是。实或复有限维线性、仿射、射影空间也是光滑流形。
光滑流形中的光滑路径的每点上都有切向量,其属于流形在这一点上的切空间。n维光滑流形的切空间是n维线性空间。光滑流形上光滑函数的微分提供了切空间上每一点的线性函数。
黎曼流形或黎曼空间是切空间有内积、满足部分条件的光滑流形。欧氏空间是黎曼空间,欧氏空间中的光滑面也是黎曼空间,双曲非欧空间也是黎曼空间。黎曼空间中的曲线有长度,两点之间最短曲线的长度定义了距离,因此黎曼空间是度量空间。交于一点的两条曲线间的夹角是切线间的夹角。
若放弃切空间内积的正定性,就得到了伪黎曼流形,包括对广义相对论非常重要的洛伦兹空间。
可测、测度空间与概率空间
[编辑]
再放弃距离和角度,保留(几何体的)体积,就得到了测度。根据柯尔莫果洛夫的概率论方法,在体积之外,测度还可以是面积、长度、质量(或电荷)分布、概率分布等概念。
经典数学中的“几何体”远比一组点更有规律。几何体的边界体积为零,因此集合体的体积就是内部的体积,可以由无限立方体序列穷尽。相反,任意点集的边界体积可以非零(例如给定立方体内部所有有理点的集合)。测度论将体积概念扩展到了一大类集合,即所谓可测集。不可测集在应用中几乎从未出现过。
可测空间中给出的可测集会产生可测函数与映射。将拓扑空间转为可测空间,要赋予σ-代数。最常用的是博雷尔集的σ-代数,也有其他选择(有时也用贝尔集、普遍可测集等)。 拓扑并不由博雷尔σ-代数唯一确定;例如,可分希尔伯特空间上的赋范拓扑和弱拓扑会产生相同的博雷尔σ-代数。 σ-代数并不都是某拓扑的博雷尔σ-代数。[c] 实际上,σ-代数可由给定集合(或函数)生成,而与拓扑无关。可测空间的每个子集本身也是可测空间。
标准可测空间(也称为标准博雷尔空间)与紧空间有相似性,因而特别有用(见EoM (页面存档备份,存于互联网档案馆))。标准可测空间之间的每个双射可测映射都同构,即反映射也可测。而此类空间之间的映射可测,当且仅当图在积空间中也可测。相似地,紧可测空间之间的连续双射都是同胚映射,即逆映射也连续。当且仅当其图在积空间中为闭,此类空间之间的映射采才连续。
欧氏空间(更广义地说,是完备可分可测空间)中的每一个博雷尔集,只要赋予博雷尔σ代数,就是标准可测空间。所有不可数标准可测空间都相互同构。
测度空间是赋予了测度的可测空间。具备勒贝格测度的欧氏空间是测度空间。积分论定义了测度空间上可测函数的可积分性和积分。
测度为0的集合称为空集,是可忽略的。因此“模0同构”被定义为全测度(即有可忽略补集)子集间的同构。
概率空间也是可测空间,整个空间的测度为1。任何概率空间族(有限或无限)的积仍是概率空间;相对地,对一般测度空间,只有有限多空间的积才有定义。因此,有许多无限维概率测度(特别是高斯测度),但没有无限维勒贝格测度。
标准概率空间非常有用。其上,条件期望可视作对条件度量的积分(常规条件概率,另见离散测度)。给定两个标准概率空间,它们的测度代数 (页面存档备份,存于互联网档案馆)的同态都由某保测映射引入。标准可测空间上的概率测度都会产生标准概率空间。标准概率空间序列(有限或无限)的积还是标准概率空间。所有非元标准概率空间都互为模0同构,其中一个是具有勒贝格测度的区间(0,1)。
这些空间不那么几何。特别是,维度的概念(以各种形式)适用于所有其他空间,却不适用于可测空间、测度空间和概率空间。
非交换几何
[编辑]微积分的理论研究,即数学分析,在20世纪初开始考虑实、复值函数的线性空间。最早的例子是函数空间,每个函数空间都适用于一类问题。这些例子有许多共同特征,很快被抽象为希尔伯特空间、巴拿赫空间和更一般的拓扑向量空间。这些都是解决各种数学问题的强大工具。
巴拿赫代数的一类空间提供了最详尽的信息,是带有连续乘法运算的巴拿赫空间。早期的重要例子是测度空间X上有界可测函数的巴拿赫代数,这类函数在逐点加与标量乘法下是巴拿赫空间。有了逐点乘,它就成了一种特殊的巴拿赫空间,现称为交换冯诺依曼代数。逐点乘决定了这代数在X上平方可积函数的希尔伯特空间上的表示。冯·诺依曼的早期发现是,这种对应关系也可以反向起作用:给定一些温和的技术假设,交换诺依曼代数与希尔伯特空间上的表示一同决定了一个测度空间,而这两种构造(诺依曼代数加测度空间的表示)是互逆的。
冯·诺依曼随后提出,非交换诺依曼代数应像交换诺依曼代数一样有几何意义。他与Francis Murray共同提出了诺依曼代数的分类。直积分构造说明了如何将任何诺依曼代数分解为更简单的代数集,即因子。冯·诺依曼和Murray将因子分为三类。第一类与交换情形几乎相同;第二类和第三类表现出新的现象。第二类诺依曼代数确定了新的几何,其特殊之处在于,维数可以是任何非负实数;第三类异于前两类,经过几十年的努力,被证明与第二类因子密切相关。 与冯·诺依曼和Murray的因子分类工作同时发展起来的,还有一种略有不同的函数空间几何方法,这就是C*-代数。此处,激励性的例子是C*-代数,其中X是局部紧的豪斯多夫拓扑空间。由定义可知,这是X上连续复值函数的代数,这些函数在无穷远处消失(宽泛地说,离所选点越远,函数越趋近于零),具有逐点相加乘的运算。盖尔范德-奈马克定理表明,交换C*-代数与几何对象之间有对应关系:对某个局部紧豪斯多夫空间X来说,交换C*-代数都是形式。因此,我们有可能纯粹根据交换C*-代数研究局部紧豪斯多夫空间。非交换几何以此为灵感,研究非交换C*-代数:若有非交换空间X,则其将是非交换C*-代数;此外,若盖尔范德-奈马克定理适用于这些非实在对象,那么空间(无论紧否)将与C*-代数相同;因此,由于缺乏直接定义非交换空间的方法,非交换空间被定义为非交换C*-代数。许多标准几何工具都可用C*-代数重述,这为研究非交换C*-代数提供了几何启发。
这两个例子现在都属于非交换几何。诺依曼代数和C*-代数的具体例子分别被称为非交换测度论和非交换拓扑学。非交换几何不仅是为了追求一般性而追求,也不仅是一种好奇心。非交换空间自然产生于某些构造中,甚至不可避免,例如用风筝形和飞镖形填满平面的彭罗斯密铺。有这样一个定理:这样的密铺中,风筝和飞镖的每个有限片段出现的频率都无限多,因此不能通过观察有限部分来区分两个彭罗斯密铺。彭罗斯密铺确定了非交换C*-代数,所以可用非交换几何工具来解决。另一个例子也是微分几何中非常有趣的例子,来自流形的叶状结构。流形分割为低维子流形(叶),每片叶都与附近的叶局部平行。所有叶组成拓扑空间,但无理旋转的例子表明,经典测度论无法进入这个拓扑空间。不过,有与叶空间关联的非交换诺依曼代数,再次为本不可理解的空间赋予了良好的几何结构。
概形
[编辑]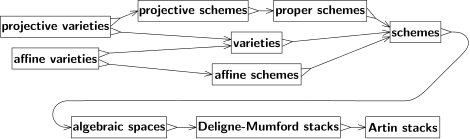
代数几何研究多项式方程的几何性质。多项式是由基本算术运算加法和乘法定义的函数,因此多项式与代数密切相关。代数几何提供了一种将几何技术应用于纯代数问题的方法,反之亦然。
在1940年代之前,代数几何只处理复数,最基本的簇是射影空间。射影空间几何与透视理论密切相关,其代数由齐次多项式描述。所有其他种类都被定义为射影空间的子集。射影簇是由一组齐次多项式定义的子集。在射影簇的每点上,集合中的所有多项式都必须等于零。线性多项式零集的补是仿射空间,仿射簇是射影簇与仿射空间的交。
安德烈·韦伊发现,几何推理有时适用于数论情形,其中的空间可能是离散的,甚至可能是有限的。为此韦伊重新阐释了代数几何的基础,使代数几何摆脱了对复数的依赖,又引入了不嵌入射影空间的抽象代数簇,现在统称为簇。
作为大多数现代代数几何基础的空间类型要比韦伊的抽象代数簇更广泛,叫做概形,由亚历山大·格罗滕迪克提出。概形论的动机之一是,多项式在函数中的结构非同寻常,代数簇因此是刚性的。在退化情形这就带来了问题。例如,圆上几乎任何一对点都能确定唯一的正割线,这两点绕圆移动时,正割线不断变化;而当两点相撞时,正割线就退化为唯一的切线,但圆上的单点这种构造的几何特征并不足以唯一确定一条线。这时,需要一种能为退化情形分配额外数据的理论。
拓扑空间是概形论的组分之一。拓扑空间具有连续函数,但过于笼统,难以反映底层代数结构。因此概形的另一个要素是拓扑空间上的层,称作“结构层”。在拓扑空间的每个开子集上,结构层制定了函数集合,称作“正则函数”(regular function)。拓扑空间和结构层必须共同满足条件:函数来自代数运算。
与流形类似,概形也被定义为以初等模型为局部近似的空间。流形中,这种初等模型是欧氏空间;概形中,这种初等模型叫做仿射概形。仿射概形提供了代数几何与交换代数的直接联系。交换代数的基本研究对象是交换环,交换环R有相应的仿射概形,将R的代数结构转为几何结构。反过来,仿射概形决定了交换环,即其结构层的全局截面的环。这两种运算互逆,因此仿射概形提供了一种研究交换代数问题的新方式。由定义,概形中的每个点都有开邻域,就是仿射概形。
仿射概形之外还有很多。特别地,射影空间满足固有性(类似于紧性)条件。仿射概形不满足固有性(非平凡情形),因此射影空间都不是仿射概形(非平凡情形)。射影概形,即射影空间的闭子概形,是最重要的一族概形。[12]
概形有一些推广的尝试。迈克尔·阿廷将代数空间定义为由定义了平展态射的等价关系构成的概形之商。代数空间保留了概形的许多有用性质,同时也更灵活,例如Keel–Mori定理可证明许多模空间都是代数空间。
比代数空间更一般的是德利涅-芒福德叠(DM stack),与概形类似,但允许出现无法完全用多项式描述的奇点。它们之于概形,好比轨形之于流形。例如,仿射平面通过绕原点旋转的有限群之商,得到不是概形也不是代数空间的DM叠。在远离原点的地方,群作用的商确定了圆上等距点的有限集;在原点处,群作用固定了这个点。在商DM叠中,这点则变为带有额外数据的商。这样的细化结构在模空间论中非常有用,最初用来描述的其实是代数曲线的模。
进一步的推广是代数叠或阿廷叠。DM叠限于有限群作用的商,虽然足以解决模理论中的许多问题,但对其他问题仍有很多限制,而阿廷叠允许更多的商。
意象
[编辑]
格罗滕迪克在研究韦伊猜想时,提出了一种新拓扑学,即格罗滕迪克拓扑。(通常意味的)拓扑空间公理化了“邻近性”概念:当且仅当两点位于许多相同的开集中时,才称它们邻近。格罗滕迪克拓扑公理化了“覆盖”概念:空间的覆盖是指共同包含环境空间所有信息的子空间集合。层是用覆盖定义的,所以格罗滕迪克拓扑也可看作层论的公理化。
格罗滕迪克的拓扑学研究使他提出的拓扑斯(意象)理论。在他的自传《收获与播种》中,他将意象称为“最广阔的概念”。[13]层(拓扑空间上的层或格罗滕迪克拓扑的层)用于表达局部数据。所有层组成的层范畴包含了表达局部数据的所有可能方式。由于拓扑空间由点构造,而点本身就是一种局部数据,因此可以用层范畴替代原始空间。因此,格罗滕迪克将意象定义为层范畴,并将意象本身作为研究对象。这些拓扑现在被称为格罗滕迪克拓扑。
每个拓扑空间都确定了一个意象,反之亦然。有些拓扑空间中,取相关的意象会丢失信息,但这些一般被认为是病态的(充分必要条件是,拓扑空间必须是索伯空间)。相反,有些意象的相关拓扑空间没有捕捉到原意象。但是这些意象远非病态,而具有极大数学意义。例如,格罗滕迪克的平展上同调论(最终导向韦伊猜想的证明)可表述为概形的平展意象的上同调,而这个意象并不来自拓扑空间。
拓扑空间常会产生特殊的意象,称为位象(locale)。拓扑空间的开子集确定了格;拓扑空间公理使得这些格成为完全海廷代数。局部论便以此为出发点。局部被定义为完全海廷代数,拓扑空间的基本性质用这些术语重新诠释、再现。局部的概念比拓扑空间更宽泛,因为索伯拓扑空间决定了唯一的局部,但许多有趣的局部并不来自拓扑空间。因为局部不需要有点,所以局部的研究称为无点拓扑。
意象还与数理逻辑有深刻联系。每个格罗滕迪克意象都有一个特殊层,称为子对象分类器,类似于所有可能真值的集合。在集合意象中,子对象分类器是集合,对应“假”与“真”;但在其他意象中,则可以更复杂。Lawver和Tierney认识到,将子对象分类器公理化,会产生一种更一般的意象,称为基本意象,是直觉主义逻辑的模型。除了提供一种将逻辑工具用于几何的强大方法外,这还使得在逻辑中使用几何方法成为可能。
空间与结构
[编辑]Kevin Carlson说:
- 这两个词[“空间”与“结构”]都没有单一数学定义。这两个词基本上可以在所有相同的情况下使用,但你通常认为“空间”偏几何,“结构”偏代数。[...]所以可以说,“结构”是做代数的地方,“空间”是做几何的地方。很多伟大的数学都来自结构到空间的传递,反之亦然,比如研究拓扑空间的基本群或环的谱。但归根结底,这种区分既不严格也不快速,而且只能到此为止:很多东西显然既是结构也是空间,有些东西显然既不是结构也不是空间,有些人很可能不同意我在这里所说的一切。[1]
尽管如此,Bourbaki还是提出了“结构”的一般定义[2],其中包含了上述几乎所有空间与(几乎?)迄今为止所有类型的数学结构,还有更多。它说明了同构的一般定义,并证明了同构结构之间的性质变换是合理的。但它从未被积极用于数学实践(甚至Bourbaki本人也是)。下面是Robert Reed[14]评论Leo Corry一本书的最后几句话:
- Corry似乎认为,结构的任何正式定义都无法公正地反映这一概念在数学实践中的应用[...]Corry的观点可以概括为,他认为“结构”本质上指的是一种做数学的方式,因此这一概念可能与数学这一文化艺术品本身一样,永远无法精确定义。
几何“空间”和代数“结构”之间的区别有时很明显,有时却难以捉摸。例如,群显然是代数,而欧几里得空间是几何。环上的模和环“一样代数”,但当环是域时,模呈现为线性空间;它是代数还是几何呢?当它在实数上、有有限维、具有内积,就变成了欧氏空间;这时是几何了。(代数的?)实数域与(几何的?)数线完全相同;(代数的?)复数域也与(几何的?)复平面完全相同,是“进行复分析的地方”,而非“做代数或做几何的地方”。
除了上面的“非交换几何”“概形”“意象”等节之外,“空间类型”一章讨论的空间都是集合(布尔巴基称其为结构的“主基集”),并被赋予了一些附加结构。基集的元素常被称为空间的“点”。相对之下,代数结构的(基集的)元素通常不会称为“点”。
不过,有时人们会使用多个主基集。例如,2维射影几何可以通过点集和线集两个基集形式化。此外,射影平面的显著特点之一是点与线作用的对称性。几何性较弱的例子:图可以由2个基集形式化,即顶点集(也称作点)和边缘集(也称作线)。布尔巴基规定,结构/空间所用的可以有有限个主基集,有有限个辅基集。。
上面的“非交换几何”“概形”“意象”等节中讨论的许多数学结构都没有规定点的基集。例如无点拓扑学/局部论从单个基集开始,其元素模仿拓扑空间中的开集(但不是点集);另见分体拓扑学。
数学空间列表
[编辑]- 仿射空间
- 拓扑空间
- 一致空间
- 豪斯道夫空间
- 巴拿赫空间
- 向量空间(或稱線性空間)
- 赋范向量空间(或稱線性賦范空間)
- 拓扑向量空间
- 内积空间
- 度量空间
- 测度空间
- 完備度量空间
- 欧几里得空间
- 希尔伯特空间
- 射影空间
- 函数空间
- 樣本空间
- 概率空间
- 代数空间
- 贝尔空间
- 伯格曼空间
- 伯克维奇空间
- 贝索夫空间
- 卡拉比–丘空间
- 康托尔空间
- 柯西空间
- 丘空间
- 闭包空间
- 共形空间
- 艾伦伯格–麦克莱恩空间
- 芬斯勒空间*第一可数空间
- 弗雷歇空间
- 几何空间
- 哈代空间
- 齐性空间
- 柯尔莫果洛夫空间
- Lp空間
- 透镜空间
- 刘维尔空间
- 局部有限空间
- 闭路空间
- 洛伦兹空间
- 闵可夫斯基空间
- 仿紧空间
- 完美胚空间
- 平面空间
- 波兰空间
- 邻近空间
- 二次空间
- 商空间
- 商空间 (线性代数)
- 序列空间
- 谢尔宾斯基空间
- 索博列夫空间
- 状态空间 (计算机空间)
- 斯通空间
- 辛向量空间
- 泰希米勒空间
- 张量空间
另见
[编辑]注释
[编辑]脚注
[编辑]- ^ 1.0 1.1 Carlson, Kevin. Difference between 'space' and 'mathematical structure'?. Stack Exchange. August 2, 2012.
- ^ 2.0 2.1 2.2 2.3 2.4 Bourbaki 1968,Chapter IV
- ^ Itô 1993,page 987
- ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 Bourbaki, Nicolas. Elements of the history of mathematics
 . Masson (original), Springer (translation). 1994. ISBN 978-3-540-64767-6. doi:10.1007/978-3-642-61693-8.
. Masson (original), Springer (translation). 1994. ISBN 978-3-540-64767-6. doi:10.1007/978-3-642-61693-8.
- ^ Gray, Jeremy. Ideas of Space: Euclidean, Non-Euclidean and Relativistic
 second. Clarendon Press. 1989. ISBN 978-0198539353.
second. Clarendon Press. 1989. ISBN 978-0198539353.
- ^ Gallier, Jean. Basics of Euclidean geometry. Geometric Methods and Applications. Texts in Applied Mathematics 38. Springer. 2011: 177–212. ISBN 978-1-4419-9960-3. doi:10.1007/978-1-4419-9961-0_6. See also OpenCourseWare (页面存档备份,存于互联网档案馆).
- ^ Pudlák, Pavel. Logical Foundations of Mathematics and Computational Complexity: A Gentle Introduction. Springer Monographs in Mathematics. Springer. 2013. ISBN 978-3-319-00118-0. doi:10.1007/978-3-319-00119-7.
- ^ Bourbaki 1968,page 385
- ^ Bourbaki 1968,Sect.IV.1.6
- ^ Bourbaki 1968,Sect.IV.1.7
- ^ Lanczos, Cornelius. Space through the Ages: The Evolution of Geometrical Ideas from Pythagoras to Hilbert and Einstein
 . Academic Press. 1970: 269. ISBN 978-0124358508.
. Academic Press. 1970: 269. ISBN 978-0124358508.
- ^ Eisenbud & Harris 2000.
- ^ "Si le thème des schémas est comme le coeur de la géométrie nouvelle, le thème du topos en est l’enveloppe, ou la demeure. Il est ce que j’ai conçu de plus vaste, pour saisir avec finesse, par un même langage riche en résonances géométriques, une "essence" commune à des situations des plus éloignées les unes des autres, provenant de telle région ou de telle autre du vaste univers des choses mathématiques." Récoltes et Semailles, page P43.
- ^ Reed, Robert C. Leo Corry, Modern Algebra and the Rise of Mathematical Structures. Review. Modern Logic. 2000, 8 (1–2): 182–190 [2023-09-28]. (原始内容存档于2020-08-08).
参考文献
[编辑]- Bourbaki, Nicolas, Elements of mathematics, Hermann (original), Addison-Wesley (translation).
- Bourbaki, Nicolas, Elements of mathematics: Theory of sets, Hermann (original), Addison-Wesley (translation), 1968.
- Eisenbud, David; Harris, Joe, The Geometry of Schemes, Springer-Verlag, 2000, ISBN 978-0-387-98638-8, doi:10.1007/b97680.
- Gowers, Timothy; Barrow-Green, June; Leader, Imre (编), The Princeton Companion to Mathematics, Princeton University Press, 2008, ISBN 978-0-691-11880-2.
- Itô, Kiyosi (编), Encyclopedic dictionary of mathematics second, Mathematical society of Japan (original), MIT press (translation), 1993.
外部链接
[编辑] 维基共享资源上的相關多媒體資源:空间
维基共享资源上的相關多媒體資源:空间- Matilde Marcolli (2009) The notion of space in mathematics (页面存档备份,存于互联网档案馆), from Caltech.







