空間 (數學)
數學上,空間是指一種具有特殊性質及一些額外結構的集合(有時稱為全集)。在初等數學或中學數學中,空間通常指三維空間。 現代數學使用了多種類型的空間,如歐幾里得空間、線性空間、拓撲空間、希爾伯特空間或概率空間,但並不存在單稱為「空間」的數學物件。[1][a]

空間由被視為點的數學物件和點之間的關係組成。 點的性質可以千差萬別:例如,點可以是集合的元素,另一個空間上的函數,也可以是另一個空間的子空間。點之間的關係決定了空間的性質,更確切地說一般認為同構空間完全相同,空間之間的同構是點之間的一一對應關係。例如,歐幾里得公理唯一確定了三維歐幾里得空間各點之間的關係,[b]所以所有三維歐幾里得空間都是相同的。
數學物件應被視為幾何「空間」還是代數「結構」,並不總是很清楚。尼古拉·布林巴基[2]提出了結構的一般定義,包括了所有常見的空間類型,提供了同構的一般證明方法,並證明了同構結構之間的性質轉移是合理的。
歷史
[編輯]| 古典 | 現代 |
|---|---|
| 公理(axiom)是定義的明顯含義 | 公理(axiom)是約定俗成的 |
| 定理(theorem)是絕對客觀的真理 | 定理(theorem)是相應公理的含義 |
| 點、線等之間的關係由其性質決定 | 點、線等之間的關係是必要的,而其性質不必要 |
| 數學物件呈現為自身結構 | 數學理論描述了數學物件的性質 |
| 幾何對應實驗現實 | 幾何是數學真理 |
| 空間的所有幾何性質都來自公理 | 空間的公理不能決定所有幾何性質 |
| 幾何是一門獨立、自主的學科 | 經典幾何是一種通用的數學語言 |
| 空間是三維的 | 不同的維度概念適用於不同類型的空間 |
| 空間是幾何的全集 | 空間只是數學結構,出現在數學的各個分支中 |
幾何學黃金時代之前
[編輯]
古希臘數學中,「空間」指日常生活中觀察到的三維現實的幾何抽象。約公元前300年,歐幾里得給出了關於空間性質的公理,將所有數學都建立在幾何基礎上,甚至通過比較線段長度來定義數字。
1637年,勒內·笛卡爾提出了直角坐標系(解析幾何)。[3]當時,幾何定理被視作可通過直覺和推理實現認識的絕對客觀真理,類似於自然科學的物件;[4]:11公理則被認為是定義的明顯含義。[4]:15
幾何圖形有兩種等價關係:全等和相似。平移、旋轉和翻折對圖形進行全等轉換,位似轉換得到相似圖形。例如,所有圓都相似,但橢圓和圓不相似。第三種等價關係由加斯帕爾·蒙日於1795年提出,出現在射影幾何中:在適當的投影轉換下,橢圓、拋物線和雙曲線都會變成圓,稱它們射影等價。
歐幾里得幾何與射影幾何之間的關係[4]:133表明,數學物件並非以結構呈現。[4]:21數學物件的性質由數學理論描述,而這些性質作為公理,是理論的基礎。[4]:20
距離和角度不會出現在射影幾何定理中,因為射影幾何公理中沒有出現這些概念,也沒有從概念中定義出來。「三角形的內角和是多少」這樣的問題,在歐幾里得幾何中有意義,但在射影幾何中則毫無意義。
19世紀出現了不同的情況:在某些幾何中,三角形內角和定義明確,但異於一般值(180°)。尼古拉·羅巴切夫斯基和鮑耶·亞諾什分別於1829年和1832年(高斯於1816年發現,未發表)[4]:133引入了非歐雙曲幾何,即內角和取決於具體的三角形,且總小於180°。歐金尼奧·貝爾特拉米(1868)、費利克斯·克萊因(1871)分別獲得了非歐雙曲幾何「模型」,從而完全證明了這理論在邏輯上的可能性。[4]:24[5]
這一發現迫使人們放棄了對歐幾里得幾何為真理的宣稱,表明公理並非「顯而易見」,也不是「定義的含義」,而是假設。它們不必匹配實驗現實,它的定理也不失為「數學真理」。[4]:15
非歐幾何的歐氏模型,是選擇歐氏空間中的物件及之間的關係,這些關係滿足非歐幾何的所有公理(因此也滿足所有定理)。這些歐氏物件和關係模仿了非歐關係,這表明在數學中,物件間的關係是必不可少的,而物件的性質卻不是。
幾何學黃金時代及之後
[編輯]英語中的幾何學一詞是geometry,來自古希臘語geo-「地」與-metron「測量」,最初指的是測量生活中空間的長度、區域的面積與體積的實用方法,後來得到了推廣。
據Bourbaki[4]:131,1795年(蒙日《畫法幾何學》)到1872年(克萊因《埃爾蘭根綱領》)這段時間可以稱為「幾何學黃金時代」。歐幾里得幾何最初研究的空間,叫做三維歐幾里得空間。歐幾里得在23個世紀之前將其公理化,後來得到了希爾伯特公理、塔斯基公理和伯克霍夫公理的重新詮釋,它們通過公理約束的原始概念(如「點」「之間」「全等」)來描述空間。
解析幾何取得了巨大進步,並成功通過轉換群不變式的計算,取代了經典幾何定理。[4]:134,5那時起,業餘數學家更關心古典幾何的新定理。[4]:136但古典幾何的遺產並沒有丟失。Bourbaki認為[4]:138「古典幾何學作為一門獨立、活躍學科的角色被超越了,因此它被轉化為當代數學的一種通用語言。」
同時,數開始取代集合成為數學的基礎。例如,理查德·戴德金的論文《連續性與無理數》(1872)斷言直線上的點應具有戴德金分割性質,因此直線與實數集是一回事。戴德金謹慎地指出,這是無法證明的假設。在現代的論述中,這通常被視為線的定義,幾何從而簡化為算術。三維歐幾里得空間被定義為仿射空間,其元素差的相關向量空間具有內積。[6]像歐幾里得那樣「從頭來」的定義現在已不常用,因為沒有揭示空間與其他空間的關係。此外,三維射影空間現在被定義為四維向量空間的所有一維子空間(即過原點的直線)的空間。基的轉變需要新的公理,如採用這些公理,幾何學經典公理就變成了定理。
現在,空間由選定的數學物件(例如,另一個空間上的函數,或另一個空間的子空間,或僅僅是集合的元素)組成,這些物件被視為點,而點之間的關係則是選定的。因此,空間只是一種方便的數學結構。可能會認為與其他數學物件相比,「空間」更具有幾何感,但事實並非總是如此。
1854年,伯恩哈德·黎曼在就職演講上指出,以n個實數為參數的數學物件可當做是n維空間中的點。[4]:140當代數學家仍遵循這一思想,並發現在幾乎所有地方使用經典幾何術語極具啟發性。[4]:138
函數是重要的數學物件,正如黎曼指出,函數一般構成無窮維的函數空間,[4]:141在20世紀的泛函分析中得到了詳細闡述。
空間的分類
[編輯]3個分類層級
[編輯]每種空間雖然都有自己的定義,但「空間」的一般概念卻無法形式化。有些結構可叫做「空間」,有些則不能,沒有明確標準。另外,「結構」也沒有能通行的定義。據Pudlák所說[7]:「數學[……]不能完全用數學結構這樣的單一概念來解釋。然而,布林巴基的結構主義方法是我們所擁有的最好的方法。」布林巴基的結構主義方法將在#空間與結構中討論,現在先按他的精神,概述空間(和結構)的可能分類。
我們將空間分為3層。鑑於每種數學理論都由屬性描述物件,那麼首先就要問:具體是哪些屬性?這是第1層(頂層)。第2層要考慮解答特別重要(在第1層有意義)的問題。在第三級分類中,則考慮所有可能問題。
例如,歐幾里得空間和射影空間的區別屬於一級分類的區別,因為兩點之間的距離在歐幾里得空間中是確定的,而在投影空間中是不確定的。「三角形內角和是多少」在歐幾里得空間中有意義,但在射影空間中無意義;在非歐空間中,這個問題也有意義,而異於歐氏空間,後者的區別便不屬於一級。歐幾里得平面與歐幾里得三維空間之間的區別也不是一級分類的區別:「維度具體是多少」的問題,在兩種情形下都有意義。
二級分類可以區分歐氏空間和非歐空間、有限維空間和無限維空間、緊空間和非緊空間等。用布林巴基的話說,[2]二級分類是按「種」分類,不過與生物分類不同,一個空間可能屬於多個「種」。
三級分類區分不同維度的空間,但不區分歐幾里得平面和所有實數對的集合(都是二維歐氏空間)。更正式地說,三級分類的標準是同構。空間之間的同構定義為兩者的點之間的一一對應,保留了一級分類規定的所有關係。同構就是空間之間的等價關係。
同構的概念揭示了一級分類。給定同一一級分類的兩個空間之間的一一對應關係,便可以問這是否是同構。這個問題對於兩個不同類的空間毫無意義。
與自身同構,稱為自同構。歐氏空間的自同構是平移、旋轉、反射和它們的組合。同維歐氏空間都是同質的,因為每個點都可以通過自同構轉換成其他每個點。
歐幾里得公理[b]沒留下自由的空間,唯一決定了空間的所有幾何屬性。更確切地說,所有三維歐氏空間都互相同構。用Bourbaki的話來說,相應的理論是唯一等價(「單價」)的。相對地,拓撲空間之間通常不同構,理論是「多價的」。類似想法也見於數理邏輯:範疇理論的所有同勢模型都相互同構。Bourbaki[8]認為,對多價理論的研究是現代數學區別於古典數學的顯著特徵。
空間種類之間的關係
[編輯]拓撲概念(連續、收斂、開集、閉集等等)在歐氏空間中有自然的定義,也就是說歐氏空間都是拓撲空間。兩個歐氏空間之間的同構也是相應拓撲空間的同構(同胚),但反過來就不是了:同胚可能會使距離改變。用布林巴基的話說[2],「拓撲空間」是「歐氏空間」結構的內在結構。類似觀點見於範疇論:歐氏空間範疇是拓撲空間範疇上的具體範疇;遺忘函子將前者映射到後者。
3維歐氏空間是歐氏空間的特例。用布林巴基的話說,[2]3維歐氏空間「種」要比歐氏空間「種」更豐富。同樣,緊拓撲空間的種類也比拓撲空間的種類豐富。
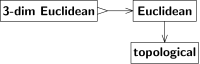
如圖3所示,空間種類的此種關係可用圖表示。A到B的箭頭意味着,A空間也是B空間;或可視作B空間;或提供了B空間,等等。將A和B視作空間種類,可以將箭頭解釋為A到B的轉化(用Bourbaki的話說[9]「從A空間到B空間的推導過程」。除非A、B是集合類,否則不完全是函數;這一細微差別不會影響下面的討論)。圖3的兩個箭頭都不可逆,但原因不同。
「歐幾里得」到「拓撲」的過程是遺忘的。拓撲區分連續與不連續,但不分直線和曲線。直覺告訴我們,歐幾里得結構無法從拓撲中復原。可以證明拓撲空間的自同構(即自同胚)不同於歐幾里得空間的自同構(即不是平移、旋轉和反射的組合)。這樣的轉換會改變(不過仍然同構)給定的歐氏結構,而前後的歐氏結構都對應單一拓撲結構。
相比之下,從「3維歐氏」到「歐氏」空間的轉換就不是遺忘的;後者不一定是3維的,但若恰好是3維的,則不會丟失任何結構。後一種轉換是單射(一到一),而前一種轉換不是(多到一)。我們用尾部帶鈎的箭頭「↣」表示單射。
兩種轉換都不是滿射,即並非每個B空間都來自A空間。首先,3維歐氏空間是歐氏空間的特例而非通例;其次,歐氏空間的拓撲是拓撲的特例(例如,必須是非緊連通的,等等)。記滿射為雙頭箭頭「↠」,例子見圖4;其中「實線性拓撲」到「實線性」的箭頭是雙頭的,因為每個實線性空間都有一些(至少一個)與線性結構兼容的拓撲。
這種拓撲一般來說不唯一,但當實線性空間為有限維時唯一。對這些空間而言,轉換既是單射也是對射,即對射;如圖4中「有限維實線性拓撲」到「有限維實線性」的箭頭;逆轉換也存在(表示為反向箭頭)。因此,這兩種結構等價。在實踐中,一般不區分等價的結構種類。[10]等價結構可被視為單一結構,如圖4的大框所示。
箭頭表示的轉換服從同構,也就是說兩個同構A空間會產生兩個同構B空間。
圖4上的圖是交換圖:圖中同始同終的有向路徑都會導向相同的結果。除了圖9中的虛線箭頭外,下面的其他圖也是交換圖。「拓撲」到「可測」的箭頭是虛線,原因是:「為將拓撲空間轉為可測空間,需要賦予一個σ代數。最常用的是博雷爾集的σ代數,也有其他選擇。」實箭頭表示平凡的所謂「典型」轉換,自然而然地提出並廣泛使用。例如,在歐氏空間上討論連續函數時,無需說明其拓撲結構。事實上存在其他拓撲結構,如細拓撲;但這些拓撲結構總是明確指定的,因為它們遠不如常用的拓撲結構引人注目。虛線箭頭表示有幾種拓撲結構在使用,但沒有一種很普遍。
空間類型
[編輯]線性空間與拓撲空間
[編輯]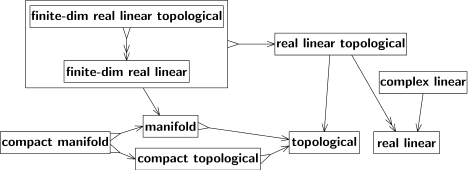
線性空間具有代數性質,有實線性空間(實數域上)、複線性空間(複數域上),以及更一般的任意域上的線性空間。複線性空間也是實線性空間(後者是前者的基),例如一維複線性空間的複數平面可以同構轉換為二維實線性空間;實線則只能被視作一維實線性空間。更一般地說,域上的向量空間也具有子體上的向量空間的結構。
根據定義,線性空間中的線性運算產生了直線(及平面等線性子空間)、平行線、橢圓(及橢球)等概念。但是無法定義正交(垂直),也找不到圓,因為線性空間中沒有純量積那樣的結構來測量角度。線性空間的維度是線性獨立向量的最大數目,也等價於跨空間的向量的最小數目;這個數可能是無限的。同一域上的兩個線性空間只有在維度相同時才同構;n維複線性空間也是2n維實線性空間。
拓撲空間具有分析性質。根據其定義,拓撲空間中的開集可引出連續函數、路徑、映射;收斂數列、極限;內部、邊界、外部等概念。而均勻連續、有界集、柯西序列、可微函數(路徑、映射)則仍未定義。拓撲空間之間的同構叫做同胚,它們是兩個方向上連續的一一對應關係。開區間(0,1)與整條數線(−∞,∞)同胚,但與閉區間[0,1]、與圓則不同胚。正方體表面與球面同胚,但不與環面同胚。不同維度的歐氏空間不同胚,這一點似乎顯而易見,卻不易證明。拓撲空間的維度也難以定義,有歸納維數(圖形的邊界維度通常比圖形維度小1的歸納)和拓撲維數等。對n維歐氏空間,兩者都等於n。
拓撲空間的子集仍是拓撲空間(相對地,線性空間只有線性子集仍是線性空間)。點集拓撲學研究的任意拓撲空間種類繁多,無法進行基於同胚的完整分類。緊拓撲空間是一種重要的拓撲空間(此類中的一種),其上的連續函數都有界。閉區間[0,1]與擴展實數線[−∞,∞]都是緊空間;開區間(0,1)和數線(−∞,∞)則不是。幾何拓撲學研究流形(此類中的另一種),它們與歐氏空間局部同胚(並滿足一些額外條件)。低維流形在同胚意義上有完全的分類。
線性結構和拓撲結構都蘊含於拓撲向量空間(或拓撲線性空間)結構。線性拓撲空間是具有連續線性運算的拓撲空間,因此,同樣是拓撲的線性空間一般不是線性拓撲空間。
有限維線性空間都是線性拓撲空間,因為其中只有一種拓撲結構,使其成為線性拓撲空間。因此「有限維線性空間」與「有限維線性拓撲空間」等價,所以有限維線性拓撲空間的可逆線性轉換都是同胚轉換。對有限維實線性空間,這三個維度概念(1個代數維度與2個拓撲維度)是一致的;但在無限維空間中,不同拓撲結構可以符合給定的線性結構,可逆線性轉換一般不是同胚轉換。
仿射與射影空間
[編輯]
通過線性空間引入仿射空間和射影空間 是很方便的,具體如下。n+1維線性空間的n維線性子空間與原空間不同類,包含一個特殊點:原點。用外部向量移動它,就得到n維仿射子空間,這是同累轉換。仿射空間不必包含於線性空間中,但與某線性空間的仿射子空間同構。給定域上的所有n維仿射空間都互相同構,用約翰·拜艾茲的話說:「仿射空間是忘記了原點的向量空間。」特別地,線性空間都是仿射空間。
給定n+1維線性空間L中的n維仿射子空間A,A中直線可定義為A與L的二維線性子空間(不與A平行的過原點平面)的交。更一般地說,A的k維仿射子空間是A與同A相交的L的k+1維線性子空間的交。
仿射子空間A的每點都是A與L的一維線性子空間的交點。但L的一部分一維子空間與A平行,可以說它們相交於無窮遠。根據定義,(n+1)維線性空間的所有一維線性子空間的集合,是n維射影空間;仿射子空間A則作為合適子集,嵌入在射影空間中。但射影空間本身是同類的。射影空間中的直線對應(n+1)維線性空間的2維線性子空間;更一般地說,射影空間的k維射影子空間對應(n+1)維線性空間的(k+1)維線性子空間,且與k維射影空間同構。
這樣,仿射空間和射影空間具有代數性質;它們可以是實空間、複空間,可以是任何域上的空間。
實或復仿射空間或射影空間也是拓撲空間。仿射空間是非緊流形,而射影空間是緊流形。在實射影空間中,直線與圓同胚,因此是緊的,這與仿射空間線性中的直線不同。
度量空間與均勻空間
[編輯]
度量空間定義了點之間的距離。度量空間之間的同構稱為等距(isometry)。度量空間是拓撲空間;若拓撲空間可蘊含於度量空間,稱拓撲空間可度量。所有流形都可度量。
度量空間中,可以定義閉集和柯西序列。稱所有柯西序列收斂的度量空間為完備空間。不完備空間都作為稠密集,嵌入到某個完備空間中;緊度量空間都是完備空間;數線是非緊完備空間;開區間(0,1)不完備。
歐氏空間都是完備空間。此外,歐氏空間的所有幾何概念都可用度量描述。例如,連接兩定點A、C的直線段由所有點B組成,這樣|AC|等於|AB|+|BC|。
郝斯多夫維數(與覆蓋給定集的小球數有關)適用於度量空間,可以不是整數(如分形)。n維歐氏空間的郝斯多夫維數都是n。
均勻空間沒有距離,但仍允許均勻連續與柯西序列(或柯西濾子或柯西網)、緊與完備。均勻空間都是拓撲空間;線性拓撲空間(無論可否度量)也是均勻空間,在有限維時完備,在無限維時通常不完備。更一般地說,交換拓撲群都是均勻空間。非交換拓撲群則蘊含左不變、右不變兩個一致結構。
賦範空間、巴拿赫空間、內積空間與希爾伯特空間
[編輯]
歐氏空間中的向量構成線性空間,但每個向量x都有長度,即範數。具有範數的實或複線性空間就是賦範空間。賦範空間既是線性拓撲空間,又是度量空間。巴拿赫空間是完備賦範空間,許多序列或函數的空間都是無窮維巴拿赫空間。 範數<1的所有向量之集構成賦範空間的單位球,是凸的中心對稱集,一般不是橢球,可能是多邊形(平面上),或更一般地是多面體(在任意有限維上)。平行四邊形法則
在賦範空間中通常不適用,但在歐氏空間中對向量成立,因為向量的歐氏平方範數是它與自身的內積:.
內積空間是實或複線性空間,具有雙線性或半雙線性形式,滿足某些條件,稱為內積。內積空間都是賦範空間。當且僅當賦範空間滿足平行四邊形法則,或其單位球是橢球時,它才蘊含於內積空間。內積空間定義了向量夾角。 希爾伯特空間是完備內積空間(有人堅稱其必須是複空間,另一些人也承認實希爾伯特空間) 。許多序列或函數的空間都是無窮維希爾伯特空間。希爾伯特空間在量子力學中非常重要。[11] n維線性實內積空間都互相同構。可以說,n維歐氏空間就是無原點的n維實內積空間。
光滑流形與黎曼流形
[編輯]
光滑流形不叫做「空間」但可以是。光滑流形都是拓撲流形,可以嵌入有限維線性空間。有限維線性空間中的光滑面是光滑流形:例如,橢球面是光滑流形,而多面體表面則不是。實或復有限維線性、仿射、射影空間也是光滑流形。
光滑流形中的光滑路徑的每點上都有切向量,其屬於流形在這一點上的切空間。n維光滑流形的切空間是n維線性空間。光滑流形上光滑函數的微分提供了切空間上每一點的線性函數。
黎曼流形或黎曼空間是切空間有內積、滿足部分條件的光滑流形。歐氏空間是黎曼空間,歐氏空間中的光滑面也是黎曼空間,雙曲非歐空間也是黎曼空間。黎曼空間中的曲線有長度,兩點之間最短曲線的長度定義了距離,因此黎曼空間是度量空間。交於一點的兩條曲線間的夾角是切線間的夾角。
若放棄切空間內積的正定性,就得到了偽黎曼流形,包括對廣義相對論非常重要的洛倫茲空間。
可測、測度空間與概率空間
[編輯]
再放棄距離和角度,保留(幾何體的)體積,就得到了測度。根據科摩哥洛夫的概率論方法,在體積之外,測度還可以是面積、長度、質量(或電荷)分佈、概率分佈等概念。
經典數學中的「幾何體」遠比一組點更有規律。幾何體的邊界體積為零,因此集合體的體積就是內部的體積,可以由無限立方體序列窮盡。相反,任意點集的邊界體積可以非零(例如給定立方體內部所有有理點的集合)。測度論將體積概念擴展到了一大類集合,即所謂可測集。不可測集在應用中幾乎從未出現過。
可測空間中給出的可測集會產生可測函數與映射。將拓撲空間轉為可測空間,要賦予σ-代數。最常用的是博雷爾集的σ-代數,也有其他選擇(有時也用貝爾集、普遍可測集等)。 拓撲並不由博雷爾σ-代數唯一確定;例如,可分希爾伯特空間上的賦範拓撲和弱拓撲會產生相同的博雷爾σ-代數。 σ-代數並不都是某拓撲的博雷爾σ-代數。[c] 實際上,σ-代數可由給定集合(或函數)生成,而與拓撲無關。可測空間的每個子集本身也是可測空間。
標準可測空間(也稱為標準博雷爾空間)與緊空間有相似性,因而特別有用(見EoM (頁面存檔備份,存於互聯網檔案館))。標準可測空間之間的每個對射可測映射都同構,即反映射也可測。而此類空間之間的映射可測,當且僅當圖在積空間中也可測。相似地,緊可測空間之間的連續對射都是同胚映射,即逆映射也連續。當且僅當其圖在積空間中為閉,此類空間之間的映射采才連續。
歐氏空間(更廣義地說,是完備可分可測空間)中的每一個博雷爾集,只要賦予博雷爾σ代數,就是標準可測空間。所有不可數標準可測空間都相互同構。
測度空間是賦予了測度的可測空間。具備勒貝格測度的歐氏空間是測度空間。積分論定義了測度空間上可測函數的可積分性和積分。
測度為0的集合稱為空集,是可忽略的。因此「模0同構」被定義為全測度(即有可忽略補集)子集間的同構。
概率空間也是可測空間,整個空間的測度為1。任何概率空間族(有限或無限)的積仍是概率空間;相對地,對一般測度空間,只有有限多空間的積才有定義。因此,有許多無限維概率測度(特別是高斯測度),但沒有無限維勒貝格測度。
標準概率空間非常有用。其上,條件期望值可視作對條件度量的積分(常規條件概率,另見離散測度)。給定兩個標準概率空間,它們的測度代數 (頁面存檔備份,存於互聯網檔案館)的同態都由某保測映射引入。標準可測空間上的概率測度都會產生標準概率空間。標準概率空間序列(有限或無限)的積還是標準概率空間。所有非元標準概率空間都互為模0同構,其中一個是具有勒貝格測度的區間(0,1)。
這些空間不那麼幾何。特別是,維度的概念(以各種形式)適用於所有其他空間,卻不適用於可測空間、測度空間和概率空間。
非交換幾何
[編輯]微積分的理論研究,即數學分析,在20世紀初開始考慮實、複值函數的線性空間。最早的例子是函數空間,每個函數空間都適用於一類問題。這些例子有許多共同特徵,很快被抽象為希爾伯特空間、巴拿赫空間和更一般的拓撲向量空間。這些都是解決各種數學問題的強大工具。
巴拿赫代數的一類空間提供了最詳盡的資訊,是帶有連續乘法運算的巴拿赫空間。早期的重要例子是測度空間X上有界可測函數的巴拿赫代數,這類函數在逐點加與純量乘法下是巴拿赫空間。有了逐點乘,它就成了一種特殊的巴拿赫空間,現稱為交換馮諾依曼代數。逐點乘決定了這代數在X上平方可積函數的希爾伯特空間上的表示。馮·諾依曼的早期發現是,這種對應關係也可以反向起作用:給定一些溫和的技術假設,交換諾依曼代數與希爾伯特空間上的表示一同決定了一個測度空間,而這兩種構造(諾依曼代數加測度空間的表示)是互逆的。
馮·諾依曼隨後提出,非交換諾依曼代數應像交換諾依曼代數一樣有幾何意義。他與Francis Murray共同提出了諾依曼代數的分類。直積分構造說明了如何將任何諾依曼代數分解為更簡單的代數集,即因子。馮·諾依曼和Murray將因子分為三類。第一類與交換情形幾乎相同;第二類和第三類表現出新的現象。第二類諾依曼代數確定了新的幾何,其特殊之處在於,維數可以是任何非負實數;第三類異於前兩類,經過幾十年的努力,被證明與第二類因子密切相關。 與馮·諾依曼和Murray的因子分類工作同時發展起來的,還有一種略有不同的函數空間幾何方法,這就是C*-代數。此處,激勵性的例子是C*-代數,其中X是局部緊的郝斯多夫拓撲空間。由定義可知,這是X上連續複值函數的代數,這些函數在無窮遠處消失(寬泛地說,離所選點越遠,函數越趨近於零),具有逐點相加乘的運算。蓋爾范德-奈馬克定理表明,交換C*-代數與幾何物件之間有對應關係:對某個局部緊郝斯多夫空間X來說,交換C*-代數都是形式。因此,我們有可能純粹根據交換C*-代數研究局部緊郝斯多夫空間。非交換幾何以此為靈感,研究非交換C*-代數:若有非交換空間X,則其將是非交換C*-代數;此外,若蓋爾范德-奈馬克定理適用於這些非實在物件,那麼空間(無論緊否)將與C*-代數相同;因此,由於缺乏直接定義非交換空間的方法,非交換空間被定義為非交換C*-代數。許多標準幾何工具都可用C*-代數重述,這為研究非交換C*-代數提供了幾何啟發。
這兩個例子現在都屬於非交換幾何。諾依曼代數和C*-代數的具體例子分別被稱為非交換測度論和非交換拓撲學。非交換幾何不僅是為了追求一般性而追求,也不僅是一種好奇心。非交換空間自然產生於某些構造中,甚至不可避免,例如用風箏形和飛鏢形填滿平面的彭羅斯密鋪。有這樣一個定理:這樣的密鋪中,風箏和飛鏢的每個有限片段出現的頻率都無限多,因此不能通過觀察有限部分來區分兩個彭羅斯密鋪。彭羅斯密鋪確定了非交換C*-代數,所以可用非交換幾何工具來解決。另一個例子也是微分幾何中非常有趣的例子,來自流形的葉狀結構。流形分割為低維子流形(葉),每片葉都與附近的葉局部平行。所有葉組成拓撲空間,但無理旋轉的例子表明,經典測度論無法進入這個拓撲空間。不過,有與葉空間關聯的非交換諾依曼代數,再次為本不可理解的空間賦予了良好的幾何結構。
概形
[編輯]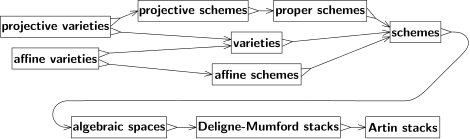
代數幾何研究多項式方程的幾何性質。多項式是由基本算術運算加法和乘法定義的函數,因此多項式與代數密切相關。代數幾何提供了一種將幾何技術應用於純代數問題的方法,反之亦然。
在1940年代之前,代數幾何只處理複數,最基本的簇是射影空間。射影空間幾何與透視理論密切相關,其代數由齊次多項式描述。所有其他種類都被定義為射影空間的子集。射影簇是由一組齊次多項式定義的子集。在射影簇的每點上,集合中的所有多項式都必須等於零。線性多項式零集的補是仿射空間,仿射簇是射影簇與仿射空間的交。
安德烈·韋伊發現,幾何推理有時適用於數論情形,其中的空間可能是離散的,甚至可能是有限的。為此韋伊重新闡釋了代數幾何的基礎,使代數幾何擺脫了對複數的依賴,又引入了不嵌入射影空間的抽象代數簇,現在統稱為簇。
作為大多數現代代數幾何基礎的空間類型要比韋伊的抽象代數簇更廣泛,叫做概形,由亞歷山大·格羅滕迪克提出。概形論的動機之一是,多項式在函數中的結構非同尋常,代數簇因此是剛性的。在退化情形這就帶來了問題。例如,圓上幾乎任何一對點都能確定唯一的正割線,這兩點繞圓移動時,正割線不斷變化;而當兩點相撞時,正割線就退化為唯一的切線,但圓上的單點這種構造的幾何特徵並不足以唯一確定一條線。這時,需要一種能為退化情形分配額外數據的理論。
拓撲空間是概形論的組分之一。拓撲空間具有連續函數,但過於籠統,難以反映底層代數結構。因此概形的另一個要素是拓撲空間上的層,稱作「結構層」。在拓撲空間的每個開子集上,結構層制定了函數集合,稱作「正則函數」(regular function)。拓撲空間和結構層必須共同滿足條件:函數來自代數運算。
與流形類似,概形也被定義為以初等模型為局部近似的空間。流形中,這種初等模型是歐氏空間;概形中,這種初等模型叫做仿射概形。仿射概形提供了代數幾何與交換代數的直接聯繫。交換代數的基本研究物件是交換環,交換環R有相應的仿射概形,將R的代數結構轉為幾何結構。反過來,仿射概形決定了交換環,即其結構層的全局截面的環。這兩種運算互逆,因此仿射概形提供了一種研究交換代數問題的新方式。由定義,概形中的每個點都有開鄰域,就是仿射概形。
仿射概形之外還有很多。特別地,射影空間滿足固有性(類似於緊性)條件。仿射概形不滿足固有性(非平凡情形),因此射影空間都不是仿射概形(非平凡情形)。射影概形,即射影空間的閉子概形,是最重要的一族概形。[12]
概形有一些推廣的嘗試。米高·阿廷將代數空間定義為由定義了平展態射的等價關係構成的概形之商。代數空間保留了概形的許多有用性質,同時也更靈活,例如Keel–Mori定理可證明許多模空間都是代數空間。
比代數空間更一般的是德利涅-芒福德疊(DM stack),與概形類似,但允許出現無法完全用多項式描述的奇異點。它們之於概形,好比軌形之於流形。例如,仿射平面通過繞原點旋轉的有限群之商,得到不是概形也不是代數空間的DM疊。在遠離原點的地方,群作用的商確定了圓上等距點的有限集;在原點處,群作用固定了這個點。在商DM疊中,這點則變為帶有額外數據的商。這樣的細化結構在模空間論中非常有用,最初用來描述的其實是代數曲線的模。
進一步的推廣是代數疊或阿廷疊。DM疊限於有限群作用的商,雖然足以解決模理論中的許多問題,但對其他問題仍有很多限制,而阿廷疊允許更多的商。
意象
[編輯]
格羅滕迪克在研究韋伊猜想時,提出了一種新拓撲學,即格羅滕迪克拓撲。(通常意味的)拓撲空間公理化了「鄰近性」概念:當且僅當兩點位於許多相同的開集中時,才稱它們鄰近。格羅滕迪克拓撲公理化了「覆蓋」概念:空間的覆蓋是指共同包含環境空間所有資訊的子空間集合。層是用覆蓋定義的,所以格羅滕迪克拓撲也可看作層論的公理化。
格羅滕迪克的拓撲學研究使他提出的拓撲斯(意象)理論。在他的自傳《收穫與播種》中,他將意象稱為「最廣闊的概念」。[13]層(拓撲空間上的層或格羅滕迪克拓撲的層)用於表達局部數據。所有層組成的層範疇包含了表達局部數據的所有可能方式。由於拓撲空間由點構造,而點本身就是一種局部數據,因此可以用層範疇替代原始空間。因此,格羅滕迪克將意象定義為層範疇,並將意象本身作為研究物件。這些拓撲現在被稱為格羅滕迪克拓撲。
每個拓撲空間都確定了一個意象,反之亦然。有些拓撲空間中,取相關的意象會丟失資訊,但這些一般被認為是病態的(充分必要條件是,拓撲空間必須是索伯空間)。相反,有些意象的相關拓撲空間沒有捕捉到原意象。但是這些意象遠非病態,而具有極大數學意義。例如,格羅滕迪克的平展餘調論(最終導向韋伊猜想的證明)可表述為概形的平展意象的餘調,而這個意象並不來自拓撲空間。
拓撲空間常會產生特殊的意象,稱為位象(locale)。拓撲空間的開子集確定了格;拓撲空間公理使得這些格成為完全海廷代數。局部論便以此為出發點。局部被定義為完全海廷代數,拓撲空間的基本性質用這些術語重新詮釋、再現。局部的概念比拓撲空間更寬泛,因為索伯拓撲空間決定了唯一的局部,但許多有趣的局部並不來自拓撲空間。因為局部不需要有點,所以局部的研究稱為無點拓撲。
意象還與數理邏輯有深刻聯繫。每個格羅滕迪克意象都有一個特殊層,稱為子物件分類器,類似於所有可能真值的集合。在集合意象中,子物件分類器是集合,對應「假」與「真」;但在其他意象中,則可以更複雜。Lawver和Tierney認識到,將子物件分類器公理化,會產生一種更一般的意象,稱為基本意象,是直覺主義邏輯的模型。除了提供一種將邏輯工具用於幾何的強大方法外,這還使得在邏輯中使用幾何方法成為可能。
空間與結構
[編輯]Kevin Carlson說:
- 這兩個詞[「空間」與「結構」]都沒有單一數學定義。這兩個詞基本上可以在所有相同的情況下使用,但你通常認為「空間」偏幾何,「結構」偏代數。[...]所以可以說,「結構」是做代數的地方,「空間」是做幾何的地方。很多偉大的數學都來自結構到空間的遞移,反之亦然,比如研究拓撲空間的基本群或環的譜。但歸根結底,這種區分既不嚴格也不快速,而且只能到此為止:很多東西顯然既是結構也是空間,有些東西顯然既不是結構也不是空間,有些人很可能不同意我在這裏所說的一切。[1]
儘管如此,Bourbaki還是提出了「結構」的一般定義[2],其中包含了上述幾乎所有空間與(幾乎?)迄今為止所有類型的數學結構,還有更多。它說明了同構的一般定義,並證明了同構結構之間的性質轉換是合理的。但它從未被積極用於數學實踐(甚至Bourbaki本人也是)。下面是Robert Reed[14]評論Leo Corry一本書的最後幾句話:
- Corry似乎認為,結構的任何正式定義都無法公正地反映這一概念在數學實踐中的應用[...]Corry的觀點可以概括為,他認為「結構」本質上指的是一種做數學的方式,因此這一概念可能與數學這一文化藝術品本身一樣,永遠無法精確定義。
幾何「空間」和代數「結構」之間的區別有時很明顯,有時卻難以捉摸。例如,群顯然是代數,而歐幾里得空間是幾何。環上的模和環「一樣代數」,但當環是域時,模呈現為線性空間;它是代數還是幾何呢?當它在實數上、有有限維、具有內積,就變成了歐氏空間;這時是幾何了。(代數的?)實數體與(幾何的?)數線完全相同;(代數的?)複數域也與(幾何的?)複數平面完全相同,是「進行複分析的地方」,而非「做代數或做幾何的地方」。
除了上面的「非交換幾何」「概形」「意象」等節之外,「空間類型」一章討論的空間都是集合(布林巴基稱其為結構的「主基集」),並被賦予了一些附加結構。基集的元素常被稱為空間的「點」。相對之下,代數結構的(基集的)元素通常不會稱為「點」。
不過,有時人們會使用多個主基集。例如,2維射影幾何可以通過點集和線集兩個基集形式化。此外,射影平面的顯著特點之一是點與線作用的對稱性。幾何性較弱的例子:圖可以由2個基集形式化,即頂點集(也稱作點)和邊緣集(也稱作線)。布林巴基規定,結構/空間所用的可以有有限個主基集,有有限個輔基集。。
上面的「非交換幾何」「概形」「意象」等節中討論的許多數學結構都沒有規定點的基集。例如無點拓撲學/局部論從單個基集開始,其元素模仿拓撲空間中的開集(但不是點集);另見分體拓撲學。
數學空間列表
[編輯]- 仿射空間
- 拓撲空間
- 均勻空間
- 豪斯道夫空間
- 巴拿赫空間
- 向量空間(或稱線性空間)
- 賦範向量空間(或稱線性賦范空間)
- 拓撲向量空間
- 內積空間
- 度量空間
- 測度空間
- 完備度量空間
- 歐幾里得空間
- 希爾伯特空間
- 射影空間
- 函數空間
- 樣本空間
- 概率空間
- 代數空間
- 貝爾空間
- 伯格曼空間
- 伯克維奇空間
- 貝索夫空間
- 卡拉比–丘空間
- 康托爾空間
- 柯西空間
- 丘空間
- 閉包空間
- 共形空間
- 艾倫伯格–麥克萊恩空間
- 芬斯勒空間*第一可數空間
- 弗雷歇空間
- 幾何空間
- 哈代空間
- 齊性空間
- 科摩哥洛夫空間
- Lp空間
- 透鏡空間
- 萊歐維爾空間
- 局部有限空間
- 閉路空間
- 洛倫茲空間
- 閔可夫斯基空間
- 仿緊空間
- 完美胚空間
- 平面空間
- 波蘭空間
- 鄰近空間
- 二次空間
- 商空間
- 商空間 (線性代數)
- 序列空間
- 謝爾賓斯基空間
- 索博列夫空間
- 狀態空間 (計算機空間)
- 斯通空間
- 辛向量空間
- 泰希米勒空間
- 張量空間
另見
[編輯]註釋
[編輯]腳註
[編輯]- ^ 1.0 1.1 Carlson, Kevin. Difference between 'space' and 'mathematical structure'?. Stack Exchange. August 2, 2012.
- ^ 2.0 2.1 2.2 2.3 2.4 Bourbaki 1968,Chapter IV
- ^ Itô 1993,page 987
- ^ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 Bourbaki, Nicolas. Elements of the history of mathematics
 . Masson (original), Springer (translation). 1994. ISBN 978-3-540-64767-6. doi:10.1007/978-3-642-61693-8.
. Masson (original), Springer (translation). 1994. ISBN 978-3-540-64767-6. doi:10.1007/978-3-642-61693-8.
- ^ Gray, Jeremy. Ideas of Space: Euclidean, Non-Euclidean and Relativistic
 second. Clarendon Press. 1989. ISBN 978-0198539353.
second. Clarendon Press. 1989. ISBN 978-0198539353.
- ^ Gallier, Jean. Basics of Euclidean geometry. Geometric Methods and Applications. Texts in Applied Mathematics 38. Springer. 2011: 177–212. ISBN 978-1-4419-9960-3. doi:10.1007/978-1-4419-9961-0_6. See also OpenCourseWare (頁面存檔備份,存於互聯網檔案館).
- ^ Pudlák, Pavel. Logical Foundations of Mathematics and Computational Complexity: A Gentle Introduction. Springer Monographs in Mathematics. Springer. 2013. ISBN 978-3-319-00118-0. doi:10.1007/978-3-319-00119-7.
- ^ Bourbaki 1968,page 385
- ^ Bourbaki 1968,Sect.IV.1.6
- ^ Bourbaki 1968,Sect.IV.1.7
- ^ Lanczos, Cornelius. Space through the Ages: The Evolution of Geometrical Ideas from Pythagoras to Hilbert and Einstein
 . Academic Press. 1970: 269. ISBN 978-0124358508.
. Academic Press. 1970: 269. ISBN 978-0124358508.
- ^ Eisenbud & Harris 2000.
- ^ "Si le thème des schémas est comme le coeur de la géométrie nouvelle, le thème du topos en est l』enveloppe, ou la demeure. Il est ce que j』ai conçu de plus vaste, pour saisir avec finesse, par un même langage riche en résonances géométriques, une "essence" commune à des situations des plus éloignées les unes des autres, provenant de telle région ou de telle autre du vaste univers des choses mathématiques." Récoltes et Semailles, page P43.
- ^ Reed, Robert C. Leo Corry, Modern Algebra and the Rise of Mathematical Structures. Review. Modern Logic. 2000, 8 (1–2): 182–190 [2023-09-28]. (原始內容存檔於2020-08-08).
參考文獻
[編輯]- Bourbaki, Nicolas, Elements of mathematics, Hermann (original), Addison-Wesley (translation).
- Bourbaki, Nicolas, Elements of mathematics: Theory of sets, Hermann (original), Addison-Wesley (translation), 1968.
- Eisenbud, David; Harris, Joe, The Geometry of Schemes, Springer-Verlag, 2000, ISBN 978-0-387-98638-8, doi:10.1007/b97680.
- Gowers, Timothy; Barrow-Green, June; Leader, Imre (編), The Princeton Companion to Mathematics, Princeton University Press, 2008, ISBN 978-0-691-11880-2.
- Itô, Kiyosi (編), Encyclopedic dictionary of mathematics second, Mathematical society of Japan (original), MIT press (translation), 1993.
外部連結
[編輯] 維基共享資源上的相關多媒體資源:空間
維基共享資源上的相關多媒體資源:空間- Matilde Marcolli (2009) The notion of space in mathematics (頁面存檔備份,存於互聯網檔案館), from Caltech.







