潤德勒座標
相對論中,「雙曲加速參考系」[H 1][1]座標構成了平直閔考斯基時空中重要且有用的座標卡系統。[2][3][4][5]狹義相對論中,一均勻加速的物體進行所謂的雙曲運動;在其固有參考系中,該物體是靜止的。這現象可與均勻重力場相應。關於平直時空中之加速度的一般性論述,參見狹義相對論中的加速度。
本文中,光速定義為c = 1,慣性座標系為(X,Y,Z,T),雙曲座標系則為(x,y,z,t)。這類雙曲座標系可主要分為兩大類,與加速觀察者位置有關:若觀察者時間T = 0時位在X = 1/α(其中α為常數值的固有加速度,由共動的加速規測得),則雙曲座標系稱為「潤德勒座標」(或譯林德勒座標;英語:Rindler coordinates),與之相應的是「潤德勒度規」(Rindler metric)[6]若觀察者時間T = 0時位在X = 0,則雙曲座標系有時稱為「穆勒座標」(Møller coordinates)[1]或「寇特勒-穆勒座標」(Kottler-Møller coordinates),與之相應的是「寇特勒-穆勒度規」(Kottler-Møller metric)。[7]透過採用雷達座標[8],可得到一常與雙曲運動觀察者有關的替代座標卡(Chart)。雷達座標有時也稱作「拉斯座標」(Lass coordinates)[9][10] 寇特勒-穆勒座標以及拉斯座標也常標示為潤德勒座標。[11]
關於潤德勒座標的歷史,這樣的座標系在狹義相對論發表不久後即被引入,在研究雙曲運動此一概念的同時也被研究:與平直閔考斯基時空的關係如阿爾伯特·愛因斯坦(1907年,1912年)[H 2]、馬克斯·玻恩(1909年)[H 1]、阿諾·索末菲(1910年)[H 3]、馬克斯·馮·勞厄(1911年)[H 4]、亨德里克·勞侖茲(1913年)[H 5]、弗里德里希·寇特勒(1914年)[H 6]、沃夫岡·包立(1921年)[H 7]、Karl Bollert(1922年)[H 8]、Stjepan Mohorovičić(1922年)[H 9]、喬治·勒梅特(1924年)[H 10]、愛因斯坦與納森·羅森(1935年)[H 2]、Christian Møller(1943年,1952年)[H 11]、Fritz Rohrlich(1963年)[12]、哈利·拉斯(1963年)[13];與廣義相對論中平直或彎曲時空的關聯性:沃夫岡·潤德勒(1960年,1966年)[14][15]。
潤德勒參考系的特徵
[编辑]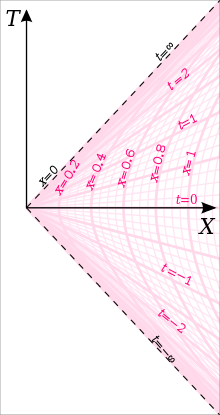
以沿-direction方向、常數值固有加速度進行雙曲運動的物體,其世界線為原時以及快度的函數,關係式為:[16]
- 。
其中為常數,為變數。這樣的世界線形態為雙曲線。阿諾·索末菲[H 3][17]展示了此方程組可重新表示為:為變數,而為常數;如此可表現出共動觀察者所測量到雙曲運動物體的「靜止型態」。設定,也就是採用了觀察者的原時作為整體雙曲加速參考系的時間,則慣性座標與雙曲座標之間的轉換式變為:[6][9]
逆轉換式為:
各種轉換式
[编辑]潤德勒觀察者
[编辑]參考文獻
[编辑]- ^ 1.0 1.1 引用错误:没有为名为
born的参考文献提供内容 - ^ 2.0 2.1 引用错误:没有为名为
Einstein的参考文献提供内容 - ^ 3.0 3.1 引用错误:没有为名为
Sommerfeld的参考文献提供内容 - ^ 引用错误:没有为名为
Laue的参考文献提供内容 - ^ 引用错误:没有为名为
Lorentz的参考文献提供内容 - ^ 引用错误:没有为名为
Kottler的参考文献提供内容 - ^ 引用错误:没有为名为
Pauli的参考文献提供内容 - ^ 引用错误:没有为名为
Bollert的参考文献提供内容 - ^ 引用错误:没有为名为
Mohoro的参考文献提供内容 - ^ 引用错误:没有为名为
Lemaitre的参考文献提供内容 - ^ 引用错误:没有为名为
Møller的参考文献提供内容
- ^ 1.0 1.1 Øyvind Grøn. Lecture Notes on the General Theory of Relativity 772. Springer. 2010: 86–91. ISBN 0387881344.
|journal=被忽略 (帮助) - ^ Misner, C. W.; Thorne, K. S.; Wheeler, J. A. Gravitation. Freeman. 1973. ISBN 0716703440.
- ^ Kopeikin,S., Efroimsky, M., Kaplan, G. Relativistic Celestial Mechanics of the Solar System. John Wiley & Sons. 2011. ISBN 3527408568.
- ^ Padmanabhan, T. Gravitation: Foundations and Frontiers. Cambridge University Press. 2010. ISBN 1139485393.
- ^ N. D. Birrell, P. C. W. Davies. Quantum Fields in Curved Space. Cambridge University Press. 1982. ISBN 1107392810.
|journal=被忽略 (帮助) - ^ 6.0 6.1 Leonard Susskind, James Lindesay. An Introduction to Black Holes, Information and the String Theory Revolution: The Holographic Universe. World Scientific. 2005: 8-10. ISBN 9812561315.
- ^ Muñoz, Gerardo; Jones, Preston. The equivalence principle, uniformly accelerated reference frames, and the uniform gravitational field. American Journal of Physics. 2010, 78 (4): 377–383. arXiv:1003.3022
 . doi:10.1119/1.3272719.
. doi:10.1119/1.3272719.
- ^ Minguzzi, E. The Minkowski metric in non-inertial observer radar coordinates. Americam Journal of Physics. 2005, 73: 1117–1121. arXiv:physics/0412024
 . doi:10.1119/1.2060716.
. doi:10.1119/1.2060716.
- ^ 9.0 9.1 David Tilbrook. General Coordinatisations of the Flat Space-Time of Constant Proper-acceleration. Australian Journal of Physics. 1997, 50 (5): 851–868. doi:10.1071/P96111.
- ^ Jones, Preston; Wanex, Lucas F. The Clock Paradox in a Static Homogeneous Gravitational Field. Foundations of Physics Letters. 2006, 19 (1): 75–85. arXiv:physics/0604025
 . doi:10.1007/s10702-006-1850-3.
. doi:10.1007/s10702-006-1850-3.
- ^ 舉例而言,Birrill & Davies (1982), pp. 110-111或Padmanabhan (2010), p. 126將方程式(2g, 2h)標示為潤德勒座標或潤德勒參考系;Tilbrook (1997) pp. 864-864 or Jones & Wanex (2006)將方程式(2a, 2b)標示為潤德勒座標。
- ^ Rohrlich, Fritz. The principle of equivalence. Annals of Physics. 1963, 22 (2): 169–191. doi:10.1016/0003-4916(63)90051-4.
- ^ Harry Lass. Accelerating Frames of Reference and the Clock Paradox. American Journal of Physics. 1963, 31 (4): 274–276. doi:10.1119/1.1969430.
- ^ Rindler, W. Hyperbolic Motion in Curved Space Time. Physical Review. 1960, 119 (6): 2082–2089. doi:10.1103/PhysRev.119.2082.
- ^ Rindler, W. Kruskal Space and the Uniformly Accelerated Frame. American Journal of Physics. 1966, 34 (12): 1174–1178. doi:10.1119/1.1972547.
- ^ Pauli, Wolfgang, Die Relativitätstheorie, Encyclopädie der mathematischen Wissenschaften, 1921, 5 (2): 539–776
In English: Pauli, W. Theory of Relativity 165. Dover Publications. 1981 [1921]. ISBN 0-486-64152-X.|journal=被忽略 (帮助) - ^ von Laue, M. Die Relativitätstheorie, Band 1 fourth edition of "Das Relativitätsprinzip”. Vieweg. 1921.; First edition 1911, second expanded edition 1913, third expanded edition 1919.
引用错误:在<references>标签中name属性为“Møller”的参考文献没有在文中使用
引用错误:在<references>标签中name属性为“Desloge”的参考文献没有在文中使用
引用错误:在<references>标签中name属性为“Dolby”的参考文献没有在文中使用
引用错误:在<references>标签中name属性为“Pauri”的参考文献没有在文中使用
引用错误:在<references>标签中name属性为“Koks”的参考文献没有在文中使用
引用错误:在<references>标签中name属性为“Blum”的参考文献没有在文中使用














