神奇形色牌
外观
| 類型 | 卡片遊戲 |
|---|---|
| 玩家數目 | 2人以上 |
| 所需技巧 | 視覺、邏輯思考、專心 |
| 牌的數量 | 81 |
| 遊戲時間 | 10-30分鐘 |
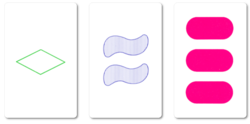
神奇形色牌(Set)是由Marsha Falco在1974年發明的卡片遊戲,由Set企業在1991年推出。神奇形色牌共有81張牌,其中有四個特徵會不同:數量(1,2,3)、圖案(菱形、橢圓形及波浪形)、紋路(實心、條紋及空心)及顏色(紅色、綠色及紫色)[1]。在一副牌中,四個特徵的組合(例如三個綠色實心的菱形)都只會出現一次,不會重覆。
歷史
[编辑]此遊戲是作者在擔任遺傳學家時,由一個編碼系統衍生而來[2]。神奇形色牌獲得1991年的門薩學會的門薩首選,在1995年德國玩家票選最佳遊戲時名列第9名。
遊戲
[编辑]
神奇形色牌的核心是組成Set的條件,只要桌面任意三張牌符合以下所有的條件,即為一個Set:
- 三張牌的數字相同,或是三張牌的數字完全不同。
- 三張牌的圖案相同,或是三張牌的圖案完全不同。
- 三張牌的紋路相同,或是三張牌的紋路完全不同。
- 三張牌的顏色相同,或是三張牌的顏色完全不同。
若有二張牌的特徵相同,但另一張牌和另外二張不同,這三張牌不能組成Set。
例如,以下的三張牌可以組成Set:
- 一個紅色實心菱形
- 二個紅色條紋菱形
- 三個紅色空心菱形
任選81張牌中的二張牌,都可以在剩下79張牌中找到一張牌,和前面的二張組成Set。
在標準的神奇形色牌遊戲中,發牌者將十二張牌放在桌上,若任一遊戲者找到一組Set,即可喊Set,並將三張牌拿走,發牌者將桌上的牌補足 ,到12張(若遊戲者喊了Set,但沒辦法很快的將三張牌拿走,會被處罰)。有可能十二張中都沒有三張牌可以組成Set,發牌者可以再發牌到15張,使讓遊戲者繼續找Set,若有需要可以再發牌到18張……。遊戲一直進行到所有的牌都發完,桌上沒有牌可以組成Set為止,此時拿到最多Set的遊戲者獲勝。
神奇形色牌也有很多不同的變體,其中包括不同的找Set方式,或是不同的遊戲者互動方式。也有許多狂熱的玩家繼續的創造遊戲的變體[3][4]。
神奇形色牌的基本組合
[编辑]- 任選兩張牌,只有一張牌可以和這兩張組成Set,因此任選三張牌,會組成Set的機率是1/79。.
- 若一直拿牌,拿到有其中有三張牌為Set為止,在拿到Set之前最多會拿到20張牌[5],這個牌組稱為maximal cap(
 A090245)。
A090245)。 - 有種不同的牌組。
- Set中有個不同特徵,個相同特徵的機率為(d=0表示所有特徵都相同,這是不可能的)。因此10%的Set會有一個特徵不一様、30%的Set會有二個特徵不一様、40%的Set會有三個特徵不一様、20%的Set所有的特徵都不一様。
- 從81張牌中拿12張牌,可能的組合為。
- 一開始拿12張牌,其中沒有Set的機率是1/30,但後面的機會就快速的增加,第四回合時約為1/14,後續的二十回合慢慢上昇到1/13,因此大部份玩遊戲的時間中,拿12張牌沒有Set的機率是1/13到1/14之間[6]。
- 在玩遊戲時,若發到15張牌,其中沒有Set的機率為1/88[6](這和任選15張牌,沒有Set的機率不同,因為只有前12張牌沒有Set時才會發到15張牌。)
- 所有遊戲中只用到十二張牌,都沒有用到十五張牌的機率約為30%[6]。
- 十二張牌中平均會有個Set,在十五張牌中平均會有個Set。
參考資料
[编辑]- ^ How to Play Set. (原始内容存档于2009-08-30).
- ^ Founder & Inventor: Marsha J. Falco 互联网档案馆的存檔,存档日期2006-10-21.
- ^ Set Variants. [2015-07-18]. (原始内容存档于2012-05-30).
- ^ Get Set - A Set Variant. [2015-07-18]. (原始内容存档于2013-04-13).
- ^ Benjamin Lent Davis and Diane MacLagan. The Card Game Set (PDF). (原始内容 (PDF)存档于2013-06-05).
- ^ 6.0 6.1 6.2 SET Probabilities Revisited. [2015-07-18]. (原始内容存档于2011-12-10).
外部連結
[编辑]- Set Enterprises (页面存档备份,存于互联网档案馆) website
- A mathematic exploration of the game Set . Including 'How many cards may be laid without creating a set', as well as investigations of different types of set games (some in the Fano plane).
- BoardGameGeek上的Set
- Sets, Planets, and Comets. (页面存档备份,存于互联网档案馆) An alternate, extended version of Set
- Simple Set Game Proof Stuns Mathematicians (页面存档备份,存于互联网档案馆) A new series of papers has settled a long-standing question related to the popular game in which players seek patterned sets of three cards.







