在物理学里,垂直轴定理(也叫“正交轴定理”)可以用来计算一片薄片的转动惯量。思考一个直角座标系,其中两个座标轴都包含与平行于此薄片;如果已知此薄片对于这两个座标轴的转动惯量,则垂直轴定则可以用来计算薄片对于第三个座标轴的转动惯量。
假设OXYZ座标系统的 X-轴与 Y-轴都包含与平行于此薄片,而 Z-轴垂直于薄片的面。 与
与  分别代表薄片对于 X-轴与 Y-轴的转动惯量.那么,薄片对于 Z-轴的转动惯量为
分别代表薄片对于 X-轴与 Y-轴的转动惯量.那么,薄片对于 Z-轴的转动惯量为
 。
。
垂直轴定理、平行轴定理、与伸展定则可以用来计算许多不同形状的物体的转动惯量。
 厚度很薄的薄片
厚度很薄的薄片
任何实际存在的刚体都有厚度;不可能有零厚度的刚体。参考右图,假设这刚体是一块很薄的薄片,厚度  是均匀的,密度也是均匀的。设定薄片的面与 XY-面共平面。那么,刚体对于 X-轴、Y-轴、与 Z-轴的转动惯量分别为
是均匀的,密度也是均匀的。设定薄片的面与 XY-面共平面。那么,刚体对于 X-轴、Y-轴、与 Z-轴的转动惯量分别为
 、
、 、
、 。
。
由于厚度超小于薄片的面尺寸,我们可以忽略  对于积分的贡献.因此,
对于积分的贡献.因此,
 、
、 。
。
所以,
 。
。
 薄圆盘
薄圆盘
a) 如右图,一个半径为  ,质量为
,质量为  的薄圆盘,对于 Z-轴的转动惯量为
的薄圆盘,对于 Z-轴的转动惯量为
 。
。
所以,对于X-轴与 Y-轴的转动惯量是
 。
。
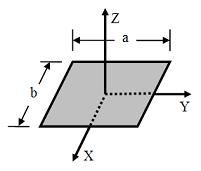 长方形薄片
长方形薄片
b) 如右图,一个尺寸为  ,质量为
,质量为  的长方形薄片,对于 X-轴、Y-轴、与 Z-轴的转动惯量分别为
的长方形薄片,对于 X-轴、Y-轴、与 Z-轴的转动惯量分别为
 、
、 、
、 。
。
很明显地,
 。
。


















