耿氏二极管
| “耿氏二极管”的各地常用名称 | |
|---|---|
| 中国大陆 | 耿氏二极管[1] |
| 台湾 | 甘恩二极体、刚氏二极体[1][2] |
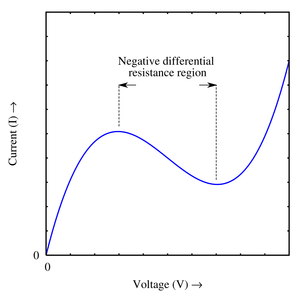
耿氏二极管(英语:Gunn diode,香港作耿氏二极体,台湾作甘恩二极体、刚氏二极体),或称转移电子器件(transferred electron device, TED)是一种在高频率电子学中应用的二极管形式。与一般的二极管同时具有N型区和P型区不同,它只由N型杂质半导体材料组成。耿氏二极管具有三个区域:两端是N型重掺杂区,介于二者中间的是一层轻掺杂的薄层。当电压施加在耿氏二极管的两端时,中央薄层处的电梯度(electrical gradients,类似电化学梯度)最大。由于在导体材料中,电流与电压成正比,导电性将会产生。最终,中央薄层处会产生较高的电场值,从而得到较高的电阻,阻止导电性的进一步增加,电流会开始下降。这意味着耿氏二极管具有负阻(Negative resistance)效应,或称负微分电阻(Negative differential resistance)。[3]
利用负微分电阻性质与中间层的时间特性,可以让直流电流通过耿氏二极管,从而形成一个弛豫振荡器(Relaxation oscillator)。在效果上,耿氏二极管中的负微分电阻会抵消的部分真实存在的正阻值,这样就可以使电路等效成一个“零电阻”的电路,从而获得无穷振荡。振荡频率部分取决于耿氏二极管的中间层,不过也可以通过改变其他外部因素来改变振荡频率。耿氏二极管被用来构造10 GHz或更高(例如太赫兹级别)的频率范围,这时共振腔常被用来控制频率。共振腔可以是波导等形式。频率以机械进行调谐(如通过改变共振腔的参数)。
用砷化镓(GaAs)材料制造的耿氏二极管可以达到200 GHz的频率,而氮化镓的耿氏二极管可以获得高达3 THz的频率。[4][5]
耿氏二极管的理论基础是耿氏效应(Gunn effect)[2],两个命名中“耿氏”都是来自于IBM物理学家J. B. 耿氏,他在1962年发现了这一效应。当时他反对将实验中的一些不连续现象视为噪声,他对这现象做了一些研究。1965年6月,贝尔实验室的Alan Chynoweth指出,只有电子在能谷间的转移可以解释这一实验现象。[3][6]对此现象的解释参见Ridley-Watkins-Hilsum[7]理论。
耿氏效应及其与Ridley-Watkins-Hilsum效应[7]的联系,在1970年的一些专著(例如转移电子器件、以及后来电荷传输非线性波动方法等领域的书籍)中被展现。[8]其他一些涉及耿氏二极管的书籍在研究过程中出版,这些资料可以在图书馆等文献机构查阅到。
参考文献
[编辑]- ^ 1.0 1.1 Gunn diode. 国家教育研究院. [2017年1月3日]. (原始内容存档于2020-10-01).
- ^ 2.0 2.1 Gunn effect. 国家教育研究院. [2017年1月3日]. (原始内容存档于2017-01-04).
- ^ 3.0 3.1 刘恩科; 朱秉升; 罗晋生. 半导体物理学(第4版). 国防工业出版社. January 1, 2010: 406页 [2000]. ISBN 978-7-118-06562-6 (中文(中国大陆)).:119-123
- ^ V. Gružinskis, J.H. Zhao, O.Shiktorov and E. Starikov, Gunn Effect and the THz Frequency Power Generation in n(+)-n-n(+) GaN Structures, Materials Science Forum, 297--298, 34--344, 1999. [1] (页面存档备份,存于互联网档案馆)
- ^ Gribnikov, Z. S., Bashirov, R. R., & Mitin, V. V. (2001). Negative effective mass mechanism of negative differential drift velocity and terahertz generation. IEEE Journal of Selected Topics in Quantum Electronics, 7(4), 630-640.
- ^ John Voelcker. The Gunn effect: puzzling over noise. IEEE Spectrum. 1989. ISSN 0018-9235.
- ^ 7.0 7.1 Ridley-Watkins-Hilsum mechanism. 国家教育研究院. [2017年1月3日]. (原始内容存档于2017-01-04).
- ^ P. J. Bulman, G. S. Hobson and B. C. Taylor. Transferred electron devices, Academic Press, New York, 1972
