双曲余弦

双曲余弦
性质
奇偶性	偶
定义域	(-∞,∞)
到达域	[1,∞)
特定值
当x=0	1
当x=+∞	+∞
当x=-∞	+∞
最大值	+∞
最小值	1
其他性质
渐近线	无
根	无实根 见双曲余弦#根一节
临界点	0
拐点	无
不动点	无

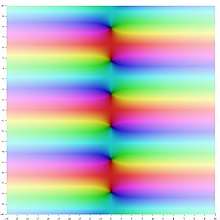
在数学中，双曲余弦是一种双曲函数，是双曲几何中，与欧几里得几何的余弦函数相对应的函数。双曲余弦一般以cosh表示，在部分较旧的文献中有时会以${\mathfrak {Cos}}$表示。双曲余弦可以用来描述悬链线，即两端固定自然下垂的绳索，因此可以用于进行悬索桥的工程计算。

定义

双曲余弦一般记为$\cosh$（有时会简写为$\operatorname {ch}$），其在复分析中定义为：

${\begin{matrix}\cosh :&\mathbb {C} &\to &\mathbb {C} \\&z&\mapsto &\displaystyle {\frac {e^{z}+e^{-z}}{2}}\end{matrix}}$

其中$z\mapsto e^{z}$是复变指数函数。

复数域双曲余弦的色相环复变函数图形

双曲余弦与自然指数函数的关联

绿色线为双曲余弦函数、蓝色线为自然指数函数、橙色线为自然指数函数的倒数。可以看到双曲余弦函数为自然指数函数与其倒数的平均数

也就是说，双曲余弦可以视为指数函数与其倒数的算术平均数，即双曲余弦为自然指数函数的偶函数部分。

在双曲几何中，双曲余弦函数类似于欧几里得几何中的余弦函数。一般的余弦可以表示为单位圆上特定角的终边正向与圆之交点的x座标；而双曲余弦则代表单位双曲线上特定双曲角的终边正向与单位双曲线之交点的x座标。 对于非单位双曲线的情形，如以下列形式定义的双曲线：

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

令$P$为双曲角的终边与双曲线的交点，并令$P'$为点$P$在共轭双曲线${\frac {y^{2}}{b^{2}}}-{\frac {x^{2}}{a^{2}}}=1$上对应的点：

$P=\left(x_{P},\,y_{P}\right)$

$P'=\left({\frac {ay_{P}}{b}},\,{\frac {bx_{P}}{a}}\right)$

此时双曲角$\alpha$可以透过交点$P$ 、共轭点$P'$与原点构成的三角形（三角形$OPP'$）与双曲扇形$OAP$的面积比来定义：

$\alpha ={\frac {\mathrm {sector} OAP}{\triangle {OPP'}}}$

在这个定义下，双曲余弦为双曲角$\alpha$的终边正向与单位双曲线之交点的x座标除以双曲线方程${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$系数$a$的结果：

$\cosh \alpha ={\frac {x_{P}}{a}}$

(a)双曲线中双曲角可透过双曲扇形QOP 与三角形$\triangle {OPP'}$的面积比定义，此时双曲余弦则为$\triangle {OQP'}$与$\triangle {OPP'}$的面积比

(b)同样地，在圆上也适用，并且对应三角函数中的余弦函数

此外，亦可以透过三角形面积比来定义双曲余弦。若右图(a)中双曲角QOP 定义为：

$u={\frac {\mathrm {sector} OPQ}{\triangle {OPP'}}}$

则其双曲余弦为：

$\cosh u={\frac {\triangle {OQP'}}{\triangle {OPP'}}}$

这个定义对应到单位圆上则可以定义一般的余弦函数。若右图(b)中角QOP 定义为：

$\theta ={\frac {\mathrm {sector} OPQ}{\triangle {OPP'}}}$

则其对应余弦为：

$\cos \theta ={\frac {\triangle {OQP'}}{\triangle {OPP'}}}$

性质

双曲余弦曲线下的面积（黄色部分）与曲线长度（红色部分）相同

双曲余弦在实数域中是连续函数，在复数域中是全纯函数，因此在整个复数域中双曲余弦处处可微，其导函数为双曲正弦函数。双曲余弦是偶函数，这意味着，双曲余弦满足以下等式：

$\cosh x=\cosh \left(-x\right)$

双曲余弦曲线下的面积（在有限区间内）总是等于该区间对应的弧长：

${\text{area}}=\int _{a}^{b}\cosh x\,dx=\int _{a}^{b}{\sqrt {1+\left({\frac {d}{dx}}\cosh x\right)^{2}}}\,dx={\text{arc length.}}$

由欧拉公式 $e^{i\theta }=\cos \theta +i\sin \theta$和双曲函数与指数函数的关联$e^{x}=\cosh x+\sinh x$能推出双曲余弦与余弦的关系：

$\cos ix=\cosh x$

特殊值

双曲余弦存在一些特殊值：

• $\cosh(0)=1$
• $\cosh(1)={\frac {e^{2}+1}{2e}}$
• $\cosh(i)=\cos(1)$
• $\cosh(\ln \varphi )={\frac {\sqrt {5}}{2}}$

其中$\varphi$为黄金比例、$e$为自然对数的底数。

根

对于不同单位复数$\omega$，$\cosh \left(\omega x\right)$的绘图，其中蓝色线为实数部、橙色线为虚数部。可以看到$\cosh \left(ix\right)$有实根，即蓝色线与橙色线同时与x轴相交

函数的根代表函数值为0的点。双曲余弦函数的根可透过求解下列方程得到：

$\cosh x=0$

在实数域中，双曲余弦的最小值为1，不与x轴相交，因此上述方程无实根。

而在复数域中可以找到双曲余弦的根。所有双曲余弦为零的点都是纯虚数：

$\cosh z=0\Leftrightarrow z\in i\pi \left(\mathbb {Z} +{\frac {1}{2}}\right).$

原因是，若将$z$表示成$x+iy$，其中$x,y$皆为实数，则由$\cosh z=\cosh x\cos y+i\sinh x\sin y$有：

$\cosh z=0\Leftrightarrow \left(\cos y=0\land \sinh x=0\right)\Leftrightarrow \left(y\in \{{\frac {\pi }{2}}+k\pi \mid k\in \mathbb {Z} \}\land x=0\right)$

例如：

$\cosh \left({\frac {\pi i}{2}}\right)=0.$

用途

物理学

主条目：悬链线

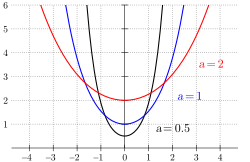
不同$a$值的悬链线函数图形

双曲余弦可以用来描述悬链线。悬链线在物理学中，可以用于描绘软绳位于水平两点间，在铅直方向均匀受力下自然形变后的形状。其可以表示为：

$y=a\cosh {\frac {x}{a}}$

其中，$y$为绳子的高度，绳子的最低点定为y轴（$x=0$），$a$是一个常数，由绳子本身性质（如密度）、与悬链线悬挂的方式决定，通常可以表示为$a={\frac {T_{0}}{g\lambda }}$，其中$g$是重力加速度、$\lambda$是绳子的密度、$T_{0}$为绳子上每一点处张力的水平分量。

建筑学

圣路易斯拱门是一个使用双曲余弦曲线设计的建筑物

双曲余弦在建筑学与工程学中一般用于计算悬索桥工程产生的悬链线。安东尼·高迪是最早将双曲余弦曲线融入建筑设计的建筑师之一，例如其作品圣家堂以及科洛尼亚桂尔教堂就有用到。

美国密苏里州圣路易的圣路易斯拱门是一个倒过来的双曲余弦曲线外型的建筑物。该拱门的最高点离地面约192米，其拱顶近似于以下方程：

$y=-39\,\mathrm {m} \cosh \left({\frac {x}{39}}\right)+231\,\mathrm {m}$

其中$\mathrm {m}$表示单位为米，且$x$满足$-96<x<96$米。而具体的几何结构由结构工程师汉斯卡尔·班德尔提供给埃罗·萨里宁的数学方程确定。

$y=A\left(\cosh {\frac {Cx}{L}}-1\right)\quad \Leftrightarrow \quad x={\frac {L}{C}}\cosh ^{-1}\left(1+{\frac {y}{A}}\right)$,

其中，常量$A$为${\frac {f_{c}}{{\frac {Q_{b}}{Q_{t}}}-1}}=\,$ 68.7672英尺（21米）、常数$C$为$\cosh ^{-1}{\frac {Q_{b}}{Q_{t}}}=3.0022$；$f_{c}=$625.0925英尺（191米）为质心的最高点、$Q_{b}=$1,262.6651 sq ft（117 m²）为截面积的最大值（在拱底取到）、$Q_{t}=$125.1406 sq ft（12 m²）为截面积的最小值（在拱顶取到）、$L=$299.2239英尺（91米）质心位于拱底之宽度的一半。

参见

• 余弦