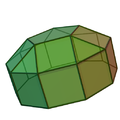
半偏方面体锥柱
外观
此条目没有列出任何参考或来源。 (2017年2月20日) |
 以五角半偏方面体锥柱为例 | ||
| 类别 | 帐塔柱 | |
|---|---|---|
| 对偶多面体 | 帐塔柱 | |
| 数学表示法 | ||
| 康威表示法 | 无法表示 | |
| 性质 | ||
| 面 | ||
| 边 | ||
| 顶点 | ||
| 欧拉特征数 | F=, E=, V= (χ=2) | |
| 组成与布局 | ||
| 面的种类 | n个鸢形 2n个四边形 2n个等腰三角形 | |
| 对称性 | ||
| 对称群 | Cnv, [n], (*nn) | |
| 旋转对称群 | Cn, [n]+, (nn) | |
| 特性 | ||
| 凸、 demi-regular | ||
| 图像 | ||
| ||
| 注:为底面边数 。 | ||
几何学中,半偏方面体锥柱的定义是指一系列的多面体,由半个偏方面体(以中间的边作为分割),一个边数两倍的不均匀柱体,以及一个边数两倍的锥体所组成,也因为如此,半偏方面体锥柱也可以视为是将半偏方面体锥拆开,中间加入一个不均匀柱体 半偏方面体锥柱的命名是根据鸢形的数量而定的,例如四角半偏方面体锥柱有四个鸢形,八个四边形以及八个等腰三角形,因此称为四角半偏方面体锥柱。 如果一个半偏方面体锥柱的鸢形皆全等,四边形全等,等腰三角形也全等的话,那么此半偏方面体锥柱则可称为正半偏方面体锥柱。
正半偏方面体锥柱
[编辑]前几个正半偏方面体锥柱为:
| 图像 | 名称 | 面的数量 |
|---|---|---|
 |
三角半偏方面体锥柱 (J18对偶) | 3个鸢形,6个四边形,6个等腰三角形 |
 |
四角半偏方面体锥柱 (J19对偶) | 4个鸢形,8个四边形,8个等腰三角形 |
 |
五角半偏方面体锥柱 (J20对偶) | 5个鸢形,10个四边形,10个等腰三角形 |
| 六角半偏方面体锥柱 | 6个鸢形,12个四边形,12个等腰三角形 |