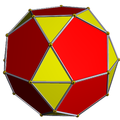
四阶十二面体

四阶十二面体

类别	拟詹森多面体
性质
面	4 正三角形 12 等腰三角形 12 正五边形
边	54
顶点	28
欧拉特征数	F=28, E=54, V=28 （χ=2）
组成与布局
顶点布局	4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5)
对称性
对称群	Td
特性
凸
图像
（对偶多面体） （展开图）

四阶十二面体是一种拟詹森多面体，因此使用全部都是正多边形的拼片仍可拼出一个四阶十二面体的模型，但面与面之间将会出现物理上可以忽略的微小空隙

在几何学中，四阶十二面体（英语：Tetrated dodecahedron），又称为四次十二面体是一种拟詹森多面体。它最早于2002年由亚历克斯·多斯基（Alex Doskey）发现，于2003年时，由罗伯特·奥斯汀（Robert Austin）独立地重新发现并命名。

四阶十二面体共有28个面，包含了12个正五边形和16个三角形，其中12个正五边形可分为四组，每组为三个相邻，等同于正十二面体的顶点；16个三角形中有四个是正三角形（以蓝色表示）和6组等腰三角形。四阶十二面体除了上述等腰三角形的底之外，所有的边皆等长，等腰三角形的底长约为该边长之1.07倍，与正三角形十分接近，因此称四阶十二面体是一种拟詹森多面体。

四阶十二面体具有四面体群的对称性。

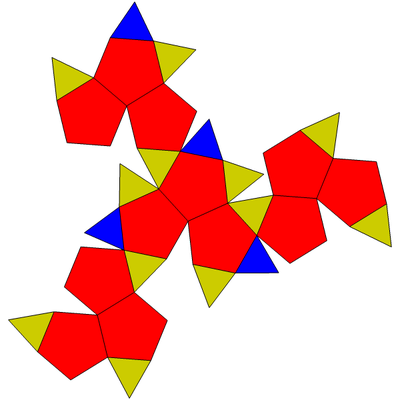
展开图

下图为四阶十二面体的展开图。在这个展开图中，12个正五边形和16个三角形根据它们于四面体对称的位置著上了颜色：

对偶多面体

四阶十二面体的对偶多面体同样是一种28面体，具有28个面、54条边以及28个顶点，但面的形状与正多边形有一些差距，由12个鸢形、12个梯形以及4个正三角形组成。

图像	展开图

相关多面体

十二面体 （柏拉图立体）	截半二十面体 （阿基米德立体）	同相双五角罩帐 （詹森多面体）

参见

• 欠四面十二面体