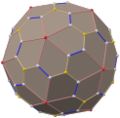
扭棱十二面体
 (单击查看旋转模型) | |||||
| 类别 | 阿基米德立体、半正多面体 | ||||
|---|---|---|---|---|---|
| 对偶多面体 | 五角六十面体 | ||||
| 识别 | |||||
| 名称 | 扭棱十二面体 | ||||
| 参考索引 | U29, C32, W18 | ||||
| 鲍尔斯缩写 | snid | ||||
| 数学表示法 | |||||
| 考克斯特符号 | |||||
| 施莱夫利符号 | sr{5,3} 或
|- !style="background-color:#e7dcc3"| || ht0,1,2{5,3} | ||||
| 威佐夫符号 | | 2 3 5 | ||||
| 康威表示法 | sD | ||||
| 性质 | |||||
| 面 | 92 | ||||
| 边 | 150 | ||||
| 顶点 | 60 | ||||
| 欧拉特征数 | F=92, E=150, V=60 (χ=2) | ||||
| 二面角 | 3-3: 164°10′31″ (164.18°) 3-5: 152°55′53″ (152.93°) | ||||
| 组成与布局 | |||||
| 面的种类 | 正三角形 正五边形 | ||||
| 面的布局 | (20+60){3}+12{5} [1] | ||||
| 顶点图 | 3.3.3.3.5 | ||||
| 对称性 | |||||
| 对称群 | I, 1/2H3, [5,3]+, (532), order 60 | ||||
| 旋转对称群 | I, [5,3]+, (532), order 60 | ||||
| 特性 | |||||
| 半正、凸、手性 | |||||
| 图像 | |||||
| |||||
在几何学中,扭棱十二面体是一种半正多面体,由正三角形和正五边形组成[2],由于其具有点可递的性质,因此属于阿基米德立体[3],也是面数最多的阿基米德立体[4],其对偶多面体为五角六十面体[5][6][7]。
命名
[编辑]这个形状最早是由克普勒以拉丁文命名的,当时克普勒给出的名称为dodecahedron simum[8][9],该名称记载于1619的《世界的和谐》。考克斯特利用扭棱十二面体不仅可以由正十二面体扭棱而成,同时也可以用正二十面体扭棱而成,因此称其为扭棱十二・二十面体(snub icosidodecahedron)或扭棱截十二面体[10]。其两种手性镜像中,左旋称为laevo[11]、右旋称为dextro[5]。
性质
[编辑]扭棱十二面体是一种阿基米德立体,为正十二面体(或正二十面体)透过扭棱变换后的结果,在施莱夫利符号中可以用[12]或sr{5,3}表示。其具有两个不同的手性几何结构,两者互为镜像[13],互相组合后可以形成均匀复合体称为二复合扭棱十二面体,其凸包为大斜方截半二十面体[14]。
构成元素
[编辑]
扭棱十二面体由92个面[15]、60个顶点和150条边组成[16],在其92个面中有80个正三角形和12个正五边形[17][18];60个顶点中,每个顶点都是4个正三角形和1个正五边形的公共顶点,在顶点图中可以用5.3.3.3.3来表示[19];150条棱中有60条棱是三角形和五边形的公共棱、90条棱是三角形和三角形的公共棱。
体积与表面积
[编辑]若扭棱十二面体边长为1,则其表面积为:
体积为:
其中 为黄金分割率,而 是三次方程式 的唯一实数解,换言之 ,其值约为 。
二面角
[编辑]扭棱十二面体有2种二面角,一种是正三角形与正三角形交角,另一种是正三角形与正五边形交角。其中正三角形与正三角形交角角度约为164.175度[11][16]:
而正三角形与正五边形交角的角度约为152.9299度[11][16]:
其中 、 定义如上。
顶点座标
[编辑]| 座标值 |
|---|
| 其中,与的定义同#二面角章节
|
若一扭棱十二面体边长为一,且质心位于原点,则其顶点座标为下列式子的偶置换:
正交投影
[编辑]扭棱十二面体有3个特殊的正交投影[2],分别为于面上投影(两种)和于棱上投影(一种),其中“在正三角形面上投影”以及“在正五边形面上投影”其对称性对应于A2 和 H2的考克斯特平面[22]。
| 投影于 | 正三角形面 | 正五边形面 | 棱 |
|---|---|---|---|
| 立体图 | 
|

|

|
| 骨架图 | 
|

|

|
| 投影对称性 | [3] | [5]+ | [2] |
| 对偶投影 | 
|

|

|
几何关联
[编辑]扭棱十二面体可以透过将正十二面体的正五边形面往外拉,直到完全不接触后,原本的顶点位置填入三角形,剩下的部分用三角形补满来构造。而将正十二面体往外拉时,在某个适当的位置时,原本正五边形与正五边形的公共棱的位置则可以摆上正方形,此时则会构成小斜方截半二十面体[23]。
而要产生扭棱的形式则需要在将正五边形面往外拉时稍微有一点旋转,并只用三角形填满空隙,而五边形旋转的方向不同可以产生手性镜像[24]。
扭棱十二面体也可以经由大斜方截半二十面体透过交错变换来构造,但构造出的扭棱十二面体并非所有面都是正多边形,其结果称为截角大斜方截半二十面体,其与扭棱十二面体有著相同的拓朴结构。
相关多面体与镶嵌
[编辑]扭棱十二面体是正十二面体(或正二十面体)经过扭棱变换后的结果,其他也是由正二十面体透过康威变换得到的多面体有:
| 对称群: [5,3], (*532) | [5,3]+, (532) | ||||||
|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

| |
| {5,3} | t0,1{5,3} | t1{5,3} | t0,1{3,5} | {3,5} | t0,2{5,3} | t0,1,2{5,3} | s{5,3} |
| 半正多面体对偶 | |||||||

|

|

|

|

|

| ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
扭棱十二面体的顶点为4个正三角形与1个正五边形的公共顶点,顶点图计为3.3.3.3.5,在考克斯特符号中可以用![]()
![]()
![]()
![]()
![]() 来表示,其中,正五边形可以替换为其他多边形,而构成一个无穷序列。其他顶点图也为4个正三角形与1个正n边形的公共顶点(顶点图:3.3.3.3.n)、考克斯特符号计为
来表示,其中,正五边形可以替换为其他多边形,而构成一个无穷序列。其他顶点图也为4个正三角形与1个正n边形的公共顶点(顶点图:3.3.3.3.n)、考克斯特符号计为![]()
![]()
![]()
![]()
![]() 的多面体如下表所示。特别地,这些几何形状都具有 (n32) 的旋转对称性,当n为6时,几何体退化成平面的无限面体,为一种半正平面镶嵌[25],n达到7或以上时,几何结构则成为双曲镶嵌图[26];而n为2时,其原像退化为三角形二面体,而n为1或更低时,则该形状不存在。
的多面体如下表所示。特别地,这些几何形状都具有 (n32) 的旋转对称性,当n为6时,几何体退化成平面的无限面体,为一种半正平面镶嵌[25],n达到7或以上时,几何结构则成为双曲镶嵌图[26];而n为2时,其原像退化为三角形二面体,而n为1或更低时,则该形状不存在。
| 扭棱镶嵌对称性 n32 的变种: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| 对称性 n32 |
球面镶嵌 | 欧氏镶嵌 | 紧凑双曲 | 仿紧双曲 | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| 考克斯特记号 | ||||||||
| 扭棱图 | 
|

|

|

|

|

|

|

|
| 顶点图 | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| 扭棱对偶 | 
|

|

|

|

|

|

| |
| 顶点布局 | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
| 原像 |  正四面体 |
 立方体 |
 正八面体 |
 正十二面体 |
 正二十面体 |
|---|---|---|---|---|---|
| 扭棱 |  扭棱四面体 sr{3,3} |

|

| ||
| 扭棱立方体 sr{4,3} |
扭棱八面体 sr{3,4} |
扭棱十二面体 sr{5,3} |
扭棱二十面体 sr{3,5} | ||
| 完全扭棱 |  完全扭棱四面体 β{3,3} |
 完全扭棱立方体 β{4,3} |
 二复合二十面体 β{3,4} |
 完全扭棱十二面体 β{5,3} |
 完全扭棱二十面体 β{3,5} |
扭棱十二面体图
[编辑]| 扭棱十二面体图 | |
|---|---|
 5阶对称性 | |
| 顶点 | 60 |
| 边 | 150 |
| 自同构群 | 60 |
| 属性 | 哈密顿、 正则 |
在图论的数学领域中,与扭棱十二面体相关的图为扭棱十二面体图,是扭棱十二面体之边与顶点的图,是一种阿基米德图[27]。由于其可以找到哈密顿回路因此也是一种哈密顿图。

|

|

|
参见
[编辑]参考文献
[编辑]- Jayatilake, Udaya. Calculations on face and vertex regular polyhedra. Mathematical Gazette. March 2005, 89 (514): 76–81.
- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Cromwell, P. Polyhedra. United Kingdom: Cambridge. 1997: 79–86 Archimedean solids. ISBN 0-521-55432-2.
- ^ 中華民國第54屆中小學科學展覽會 第三名 滾動奇跡 (PDF). 高雄市立五福国民中学. [2018-09-18]. (原始内容存档 (PDF)于2018-09-17).
- ^ 2.0 2.1 The Snub Dodecahedron. eusebeia.dyndns.org. 2018-02-06 [2018-09-16]. (原始内容存档于2018-09-16).
- ^ Cromwell, P. Polyhedra, CUP hbk (1997), pbk. (1999). Ch.2 p.79-86 Archimedean solids
- ^ ミラーボール2をつくる. d.hatena.ne.jp. [2018-10-17]. (原始内容存档于2018-10-17).
面の数は多そうだが(正五角形と正三角形の合计92)
- ^ 5.0 5.1 Weisstein, Eric W. (编). Snub dodecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Pentagonal hexecontahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ いくろ こたろ. ねじれ立方体,ねじれ12面体の双対多面体. geocities.jp. 2009-03-14 [2018-09-17]. (原始内容存档于2018-10-08) (日语).
- ^ Johannes Kepler. Harmonices Mundi. Tampachius, Linz. 1969.
- ^ Weissbach, B. and Martini, H. "On the Chiral Archimedean Solids." Contrib. Algebra and Geometry 43, 121-133, 2002.
- ^ 何永安. 阿基米德多面體的視覺化 (PDF). 中华大学 应用数学学系(所). [2018-09-18]. (原始内容存档 (PDF)于2021-08-30).
- ^ 11.0 11.1 11.2 Archimedean Solids: Snub Dodecahedron (laevo). dmccooey.com. [2018-10-17]. (原始内容存档于2018-04-01).
- ^ Wenninger, M.J. Spherical Models. Dover Publications. 2014: p.53 [2018-09-16]. ISBN 9780486143651. (原始内容存档于2018-09-16).
- ^ Snub Dodecahedron Calculator. rechneronline.de. [2018-09-16]. (原始内容存档于2018-09-16).
- ^ Skilling, John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, 79: 447–457, MR 0397554, doi:10.1017/S0305004100052440
- ^ 捩れ十二面体 [3,3,3,3,5] Snub Dodecahedron. biglobe.ne.jp. [2018-09-18]. (原始内容存档于2015-10-10).
- ^ 16.0 16.1 16.2 Archimedean Solids: Snub Dodecahedron (dextro). dmccooey.com. [2018-10-17]. (原始内容存档于2018-03-12).
- ^ Gijs Korthals Altes. Paper Snub Dodecahedron. korthalsaltes.com. [2018-09-16]. (原始内容存档于2018-09-16).
- ^ 多面体の模型. ds.cc.yamaguchi-u.ac.jp. [2018-09-16]. (原始内容存档于2018-03-19).
- ^ Robert Webb. Snub Dodecahedron. software3d.com. [2018-09-16]. (原始内容存档于2018-09-16).
- ^ Data of Snub Dodecahedron (dextro). dmccooey.com. [2018-10-17]. (原始内容存档于2017-10-31).
- ^ Data of Snub Dodecahedron (laevo). dmccooey.com. [2018-10-17]. (原始内容存档于2016-07-30).
- ^ Coxeter Planes (页面存档备份,存于互联网档案馆) and More Coxeter Planes (页面存档备份,存于互联网档案馆) 约翰·史坦布里奇
- ^ Lambert M. Surhone, Miriam T. Timpledon, Susan F. Marseken. Snub Dodecahedron. Betascript Publishing. 2010-08-12. ISBN 978-613-1-19412-2.
- ^ Popko, E.S. Divided Spheres: Geodesics and the Orderly Subdivision of the Sphere. CRC Press. 2012: 183 [2018-10-17]. ISBN 9781466504301. LCCN 2011048704. (原始内容存档于2018-10-17).
- ^ Laughlin, D.E. and Hono, K. Physical Metallurgy. Elsevier Science. 2014: 17 [2018-10-17]. ISBN 9780444537713. (原始内容存档于2018-10-17).
- ^ Klitzing, Richard. s3s7s, hyperbolic snub triheptagonal tiling. bendwavy.org. [2018-10-17]. (原始内容存档于2016-03-25).
- ^ Read, R. C.; Wilson, R. J., An Atlas of Graphs, Oxford University Press: 269, 1998
外部链接
[编辑]- 埃里克·韦斯坦因, 扭棱十二面体 (参阅阿基米德立体) 于MathWorld(英文)
- Klitzing, Richard. 3D convex uniform polyhedra s3s5s - snid. bendwavy.org.
- Editable printable net of a Snub Dodecahedron with interactive 3D view (页面存档备份,存于互联网档案馆)
- The Uniform Polyhedra (页面存档备份,存于互联网档案馆)
- Virtual Reality Polyhedra (页面存档备份,存于互联网档案馆) The Encyclopedia of Polyhedra











![{\displaystyle \xi ={\sqrt[{3}]{\frac {\varphi +{\sqrt {\varphi -{\frac {5}{27}}}}}{2}}}+{\sqrt[{3}]{\frac {\varphi -{\sqrt {\varphi -{\frac {5}{27}}}}}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddf9a9601421f1c5ac9678769b36f75c2f34ae6d)






















































