无限深方形阱

处于盒子里的粒子可以自由移动于无法穿越的阱壁内。当阱壁之间距离很微小的时候，可以观察到量子效应。例如，粒子在某位置的机率比在另外位置的机率大，粒子的能级是离散的。

在物理学里，无限深方形阱（infinite square potential），又称为无限深位势阱（infinite potential well），是一个阱内位势为 0 ，阱外位势为无限大的位势阱。思考一个或多个粒子，永远地束缚于无限深位势阱内，无法逃出。关于这些粒子的量子行为的问题，称为无限深方形阱问题，又称为无限深位势阱问题，盒中粒子问题（particle in a box problem），是一个理论问题。假若，阱内只有一个粒子，则称为单粒子无限深方形阱问题。假若，阱内有两个粒子，则称为双粒子无限深方形阱问题。假若，这两个粒子是完全相同的粒子，则问题又复杂许多，称为双全同粒子无限深方形阱问题。在这里，只讨论单粒子无限深方形阱问题。

在经典力学里，应用牛顿运动定律，可以非常容易地求得无限深方形阱问题的解答。假设粒子与阱壁的碰撞是弹性碰撞，粒子的动能保持不变。则这粒子在方形阱的两阱壁之间来回移动，碰撞来，碰撞去，而速率始终保持不变。在任意时间，粒子在阱内各个位置的机率是均匀的。

在量子力学里，这问题突然变得很有意思。许多基要的概念，在这问题的解析中，呈现了出来。由于问题的理想化与简易化，应用薛丁格方程，可以很容易地，虽然并不是很直觉地，求得解答。满足这薛丁格方程的能量本征函数，是表达粒子量子态的波函数。每一个能量本征函数的能量，只能是离散能级谱中的一个能级。很令人惊讶的是，离散能级谱中最小的能级不是 0 ，而是一个有限值，称为零点能量！这系统的最小能级量子态的能级不是 0 。

更加地，假若测量粒子的位置，则会发现粒子在阱内各个位置的机率大不相同。在有些位置，找到粒子的机率是 0 ，绝对找不到粒子。这些结果与经典力学的答案迥然不同。可是，这些结果所根据的原理，早已在许多精心设计的实验中，广泛地证明是正确无误的。

简介

一个一维无限深方形阱，阱内位势为 0 ，阱外位势为无限大。

在量子力学里，无限深方形阱问题是一个简单化的，理想化的问题。无限深方形阱是一个有限尺寸的位势阱，阱内位势为 0 ，阱外位势为无限大。在阱内，粒子感受不到任何作用力，可以自由的移动于阱内。可是，阱壁是无限的高，粒子完全地束缚于阱内。为了删繁就简，先从一维问题开始，研讨粒子只移动于一维空间的问题。之后，可推广至二维与三维空间。

这问题的薛丁格方程解答，明确地呈现出粒子的某些量子行为。这些量子行为与实验的结果相符合；可是，与经典力学的理论预测，有很大的冲突。特别令人注目地是，这量子行为是自然地从边界条件产生的，而不是人为勉强加添造成的。这解答干净俐落地展示出，任何类似波的物理系统，自然地会产生量子行为；与平常的想法恰恰相反，量子行为不是像变魔术一般变出来的。

无限深方形阱问题的粒子的量子行为包括：

1. 能量量子化：　表达粒子量子态的能量本征函数，其伴随的能量不是任意值，而只能是离散能级谱中的一个能级。
2. 零点能量：　粒子最小的允许能级，称为零点能量，不是 0 。
3. 波节点： 恰恰与经典力学相反，薛丁格方程预测会有波节的存在。这意味著在阱内某些地方，找到粒子的概率是零。

不论这问题有多么地简单，由于能够完全地解析其薛丁格方程，这问题可以导致对量子力学有更深刻的理解。实际上，这问题也非常的重要。无限深方形阱问题可以用来模拟许多真实的物理系统。例如，一个导电电子在一根直的，极细的奈米金属丝内的量子行为。更详细内容，请参阅条目奈米线。

一维阱

在一维无限深方形阱内，粒子的能级与伴随的波函数。

在一维无限深方形阱内，找到能级为 $n$ 的粒子的机率。

一个粒子束缚于一维无限深方形阱内，阱宽为 $L$ 。阱内位势为 0 ，阱外位势为无限大。粒子只能移动于束缚的方向（ $x$ 方向）。如图示，一维无限深方形阱的本征函数 $\psi _{n}$ 与本征值 $E_{n}$ 分别为

$\psi _{n}={\sqrt {\frac {2}{L}}}\sin {\left({\frac {n\pi x}{L}}\right)}$ ，

$E_{n}={\frac {n^{2}h^{2}}{8mL^{2}}}$ ；

其中，$n$ 是正值的整数，$h$ 是普朗克常数，$m$ 是粒子质量。

导引

一维不含时薛丁格方程可以表达为

$-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}\psi (x)}{\mathrm {d} x^{2}}}+V(x)\psi (x)=E\psi (x)$ ；$\quad$(1)

其中，$\psi (x)$ 是复值的、不含时间的波函数，$V(x)$ 是跟位置有关的位势，$E$ 是正值的能量。

在阱内，位势 $V(x)=0$ 。一维不含时薛丁格方程约化为

$-{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}\psi (x)}{\mathrm {d} x^{2}}}=E\psi (x)$ 。$\quad$(2)

这是一个已经经过颇多研究的二阶常微分方程。一般解本征函数 $\psi (x)$ 与本征值 $E$ 是

$\psi (x)=A\sin(kx)+B\cos(kx)$ ，$\quad$(3a)

$E={\frac {\hbar ^{2}k^{2}}{2m}}$ ；$\quad$(3b)

其中，$A$ 与 $B$ 是常数，可以是复值，$k$ 是实值的波数（因为 $E$ 是正值的，所以，$k$ 必须是实数。）。

为了求得一般解 $\psi (x)$ 的常数 $A$ ， $B$ ，与波数 $k$ 的值，必须具体表明这问题的边界条件。由于粒子趋向于位势低的地区，位势越高，找到粒子的机率 $\left|\psi (x)\right|^{2}$ 越小。在 $x=0$ ， $x=L$ 两个阱壁位置，位势无限的高，找到粒子的机率是微乎其微：$\left|\psi (x)\right|^{2}=0$ 。所以，边界条件是

$\psi (0)=\psi (L)=0$ 。(4)

代入方程 (3a) 。在 $x=0$ ，可以得到

$\psi (0)=B=0$ 。(5)

在 $x=L$ ，可以得到

$\psi (L)=A\sin(kL)=0$ 。(6)

方程 (6) 的一个简易解是 $A=0$ 。可是，这样，波函数是 $\psi =0$ 。这意味著一个不可能的物理答案：粒子不在阱内！所以，不能接受这简易解。设定 $A\neq 0$ ，则 $\sin(kL)=0$ 。那么，必须要求

$k={\frac {n\pi }{L}}$ ;(7)

其中，整数 $n>0$ 。

注意到 $n=0$ 状况必须被排除，因为，不能容许波函数是 $\psi =0$ 的物理答案：粒子不在阱内！

为了求得 $A$ 值，波函数需要归一化，一个粒子必须存在于整个一维空间的某地方：

$1=\int _{-\infty }^{\infty }\left|\psi (x)\right|^{2}\,\mathrm {d} x=\left|A\right|^{2}\int _{0}^{L}\sin ^{2}(kx)\,\mathrm {d} x=\left|A\right|^{2}{\frac {L}{2}}$ 。

常数 $A$ 的值为

$\left|A\right|={\sqrt {\frac {2}{L}}}$ 。(8)

常数 $A$ 可以是任何复数，只要绝对值等于${\sqrt {\frac {2}{L}}}$ ；可是，这些不同值的 $A$ 都对应于同样的物理状态。所以，为了方便计算，选择 $A={\sqrt {\frac {2}{L}}}$ 。

盒中粒子（黑色粗点）和自由粒子（灰色曲线）的能量都同样地跟波数有关。但是，盒中粒子只能带有离散的能量。

最后，将方程 (7) ，(8) 代入方程 (3a) ，(3b) 。一维无限深方形阱问题的能量本征方程与能量本征值（能级）是

$\psi _{n}(x)={\sqrt {\frac {2}{L}}}\sin \left({\frac {n\pi x}{L}}\right)$ ，

$E_{n}={\frac {n^{2}h^{2}}{8mL^{2}}}$ 。

• 如同前面所述，此问题只容许量子化的能级。由于 $n\neq 0$ ，最低的能级，称为零点能量，大于 0 。这答案可以用不确定原理解释。因为粒子束缚于有限的区域，位置变异数有上界。所以，粒子的动量的变异数大于 0 ，粒子必须拥有能量。这能量随著阱宽的减小而增加。

• 很重要的一点是，虽然表达粒子量子态的能量本征函数，其能量只能是离散能级谱中的一个能级。这并不能防止粒子拥有任意的能量，只要这能量大于零点能量。根据态叠加原理，粒子的量子态，可以是几个能量本征函数的叠加。当测量粒子的能量时，测量的答案，只可能是叠加的几个能级中的一个能级。由于测量会造成波函数塌缩，不能对同一个粒子做多次的测量，而指望得到有意义的答案。必须假设准备了许多同样的系统。对每一个系统内的粒子，做同样的测量。虽然，每一次的测量的答案，只可能是叠加的几个能级中的一个能级。所有答案的的平均值，是粒子的能量期望值。

启发导引

能量本征值的公式可以启发地被推导出来。试想，两个阱壁必定是波函数的波节。这意味著，阱宽必须刚好能够容纳半个波长的整数倍：

$n{\frac {\lambda }{2}}=L$ ；

其中，$\lambda$ 是波长，$n$ 是正值的整数。

应用德布罗意假说，粒子的动量 $p$ 是

$p={\frac {h}{\lambda }}={\frac {h}{2L}}n$ 。

代入联系能量与动量的经典公式，则可以得到系统的能量本征值。

$E={\frac {p^{2}}{2m}}={\frac {n^{2}h^{2}}{8mL^{2}}}$ 。

二维阱

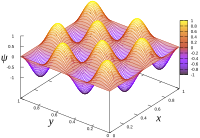二维无限深方形阱的波函数.，$n_{x}=n_{y}=4$ 。

一个粒子束缚于二维无限深方形阱内，阱宽在 $x$ 与 $y$ 方向，分别为 $L_{x}$ ，$L_{y}$ 。阱内位势为 0 ，阱外位势为无限大。粒子只能移动于束缚的方向（ $x$ 与 $y$ 方向）。二维无限深方形阱的本征函数 $\psi _{n_{x},n_{y}}$ 与本征值 $E_{n_{x},n_{y}}$ 分别为

$\psi _{n_{x},n_{y}}={\sqrt {\frac {4}{L_{x}L_{y}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)$

$E_{n_{x},n_{y}}={\frac {h^{2}}{8m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}\right]$

其中，$n_{x}$ 与 $n_{y}$ 是正值的整数。

导引

在这二维的问题里，粒子束缚于一个二维位势阱内，在阱内，二维的解答方程与方程 (2) 类似，是一个二阶偏微分方程：

$-{\frac {\hbar ^{2}}{2m}}\left({\frac {\partial ^{2}\psi }{\partial x^{2}}}+{\frac {\partial ^{2}\psi }{\partial y^{2}}}\right)=E\psi$。

应用分离变数法 。首先，假设 $\psi (x,\ y)$ 是两个不相关的函数 $X(x)$ 与 $Y(y)$ 的乘积，$X(x)$ 只含有变数 $x$ ，$Y(y)$ 只含有变数 $y$ ：

$\psi (x,y)=X(x)Y(y)$ 。

将 $\psi (x,\ y)$ 的假设方程代入二维方程，则可得到

$-{\frac {\hbar ^{2}}{2m}}\left(Y{\frac {\partial ^{2}X}{\partial x^{2}}}+X{\frac {\partial ^{2}Y}{\partial y^{2}}}\right)=EXY$ 。

将这方程两边都除以 $XY$ ，则可得到

$-{\frac {\hbar ^{2}}{2m}}\left({\frac {X''}{X}}+{\frac {Y''}{Y}}\right)=E$ 。

由于方程左边圆括号内的两个项目 ${\frac {X''}{X}}$ 、${\frac {Y''}{Y}}$ 分别只跟 $x$ 、$y$ 有关，两个项目分别都必须等于常数：

$-{\frac {\hbar ^{2}}{2m}}{\frac {X''}{X}}=E_{x}$ ，

$-{\frac {\hbar ^{2}}{2m}}{\frac {Y''}{Y}}=E_{y}$ ；

其中，$E_{x}$ 与 $E_{y}$ 都是常数，$E_{x}+E_{y}=E$ 。

这样，可以得到两个约化的一维薛丁格方程：

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}X}{dx^{2}}}=E_{x}X$ ，

$-{\frac {\hbar ^{2}}{2m}}{\frac {d^{2}Y}{dy^{2}}}=E_{y}Y$ 。

前面，已经解析了同样形式的一维薛丁格方程（方程 (2) ）。将那里的答案移接到这里，

$X_{n_{x}}={\sqrt {\frac {2}{L_{x}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)$ ，

$Y_{n_{y}}={\sqrt {\frac {2}{L_{y}}}}\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)$ ；

其中，整数 $n_{x}=1,\ 2,\ 3,\ \dots$ ，$n_{y}=1,\ 2,\ 3,\ \dots$ 。

将两个方程合并，可以得到解答：

$\psi _{n_{x},n_{y}}={\sqrt {\frac {4}{L_{x}L_{y}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)$ ，

$E_{n_{x},n_{y}}={\frac {h^{2}}{8m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}\right]$ 。

三维阱

同样地，应用分离变数法于三维阱问题，可以得到能量本征函数与能量本征值：

$\psi _{n_{x},n_{y},n_{z}}={\sqrt {\frac {8}{L_{x}L_{y}L_{z}}}}\sin \left({\frac {n_{x}\pi x}{L_{x}}}\right)\sin \left({\frac {n_{y}\pi y}{L_{y}}}\right)\sin \left({\frac {n_{z}\pi z}{L_{z}}}\right)$ ，

$E_{n_{x},n_{y},n_{z}}={\frac {h^{2}}{8m}}\left[\left({\frac {n_{x}}{L_{x}}}\right)^{2}+\left({\frac {n_{y}}{L_{y}}}\right)^{2}+\left({\frac {n_{z}}{L_{z}}}\right)^{2}\right]$ ；

其中，$n_{i}=1,\ 2,\ 3,\ \ldots$ 。

当两个以上的阱宽相等的时候，对应于同样的总能量，会存在有多个不同的波函数。这状况称为简并，是由物理系统的对称性造成的。例如，假设 一个三维阱的 $L_{x}=L_{y}$ ，则 $n_{x}=2$ ，$n_{y}=1$ ，$n_{z}=1$ 的波函数与 $n_{x}=1$ ，$n_{y}=2$ ，$n_{z}=1$ 的波函数，两个波函数的能量相等。由于在这物理系统里，有两个阱宽相等，这物理系统对称于绕著 z-轴的 $90^{\circ }$ 旋转。

参考文献

• Griffiths, David J. Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. 2004. ISBN 0-13-111892-7. 

参阅

• 态叠加原理
• 自由粒子
• 有限深方形阱
• 有限位势垒
• 球对称位势
• Delta 位势阱
• Delta 位势垒
• 量子穿隧效应
• 盒中气体
• 随机电动力学