BLAST (生物资讯学)

生物信息学中，BLAST（英语：Basic Local Alignment Search Tool）它是一个用来比对生物序列的一级结构（如不同蛋白质的氨基酸序列或不同基因的DNA序列）的算法。 已知一个包含若干序列的资料库，BLAST可以让研究者在其中寻找与其感兴趣的序列相同或类似的序列。 例如如果某种非人动物的一个以前未知的基因被发现，研究者一般会在人类基因组中做一个BLAST搜索来确认人类是否包含类似的基因（通过序列的相似性）。BLAST演算法以及实现它的程序由美国国家生物技术信息中心（NCBI）的Eugene Myers、Stephen Altschul、Warren Gish、David J. Lipman及Webb Miller博士开发的。

研究者利用BLAST来解决的其他问题有：

• 哪个细菌物种包含与氨基酸序列已知的某蛋白质有亲缘关系的蛋白质？
• 被测序的一段DNA来自哪里？
• 何种基因编码的蛋白质表现出刚刚被确定的某种结构或结构模体？

……等等。

背景

BLAST是一个被广泛使用于分析生物资讯的程式，因为它可以兼顾我们在做搜寻时的速度以及搜寻结果的精确度。因为当我们所要搜寻的目标资料库非常庞大的时候，速度就变成一项很需要考量的因素。在像BLAST和FASTA这些快速算法被开发之前，我们是使用动态规划算法来作资料库的序列搜寻，这真的非常的耗时。BLAST使用启发式搜索来找出相关的序列，在速度上比完全只使用动态规划大约快上50倍左右，不过它不像动态规划能够保证搜寻到的序列（Database sequence）和所要找的序列（Query sequence）之间的相关性，BLAST的工作就是尽可能找出资料库中和所要查询的序列相关的资讯而已，精确度稍微低一点。此外，BLAST比FASTA更快速，因为BLAST只对比较少出现或是较重要的一些关键字作更进一步的分析，而FASTA是考虑所有共同出现在所要搜寻的序列和目标序列的字。从下面介绍的演算法可以更进一步的了解。

算法

这边我们以蛋白质对蛋白质序列搜寻所用的程式BLASTP之实做的步骤，来了解BLAST这程式的主要思想。

1. 移除Query序列中之低复杂度以及有串接重复现象的区域
   低复杂度是指由很少种类的元素（如氨基酸）所组成的一个区域；而串接重复现象是指在一个Query序列中，有两段串连的区域它们组成的方式一模一样。这两种在序列中的区域可能会让BLAST找出一些虽然分数够高，但是其实和Query序列并不相关之序列，所以在我们执行搜寻之前，要先把Query序列中的这两种区域滤掉。BLAST的实际作法是，它会把这些区域用符号代替，并且在搜索的时候忽略这些符号。蛋白质序列中，就用X符号标示；而DNA序列中，则用N符号标示。低复杂度区域的部份，BLAST是用一个叫做SEG（页面存档备份，存于互联网档案馆）的程式来处理蛋白质序列，而用叫做DUST的程式来处理DNA序列。另一方面，蛋白质序列中之串接重复现象的区域则是使用XNU来处理。
2. 将Query序列中每k个字的组合做成一个表
   以k=3为例（DNA序列中，我们则常以k=11为例），我们"依序"将Query序列中每3个字的组合视为一个字组，并将这些字组列在一张字组表上，直到Query序列中最后一个字也被收入进表上为止。由图一可以更清楚的了解整个作法。

   

   图1.制作字组表的概念。

3. 列出我们所关心的所有可能之字组
   这个步骤就是BLAST和FASTA之间很重要的一点不同处。FASTA关心所有在第二步中所找出的字组表上的每一个字组，它会去搜寻资料库中的序列，看看这些序列是否含有这些字组；然而，BLAST只对高分的一些字组有兴趣，而字组的分数是由依序比较字组间的每个字，再配合得分矩阵（substitution matrix或scoring matrix）所产生的。因此，对于每一个字组而言，可能有20^3个BLAST可能关心的字组，当然这些字组经过一个门槛分数的筛选后，只有少数的字组会留下，而这些就是BLAST真正所关心的字组。举例来说，若以BLOSUM62（页面存档备份，存于互联网档案馆）为得分矩阵，则PQG分别和PEG以及PQA比较所得的分数是15以及12分，若门槛值是13，则PEG会留下来并被用于之后的步骤，而PQA则不被考虑。（在DNA序列的搜寻中，我们对于匹配的字是加5分，不匹配的则是扣4分。）
4. 将这些经筛选后剩下的高分字组组织成快速搜寻树的结构
   这是为了要让程式能快速的比对这些高分字组和资料库中的序列是否有完全匹配（exact match）的情形。
5. 对每个Query序列中的字组重复步骤1到4，并得到所有相应的高分字组
6. 扫瞄资料库中的序列，看看是否有跟剩下的高分字组完全匹配的情形
   BLAST会搜寻资料库序列中是否有高分字组出现，像是在第三步找出来的PEG。若扫瞄到有完全匹配的情形发生，那这个完全匹配的位置就会是我们之后要对Query序列和资料库序列做无间隙的区域排比（ungapped local alignment）的起点。
7. 将这些完全匹配的地方扩展为高分序对（high-scoring segment pair, HSP）
   • 旧版的BLAST会从这个匹配的位置，分别向左右去扩展，直到比对出来的分数开始变小为止。图2阐述了这个概念。

     

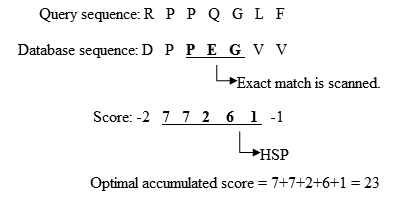
     图2.扩展匹配字组的程序

   • 为了更有效率，新版的BLAST被开发出来，叫做BLAST2或是Gapped BLAST。为了要维持搜寻的灵敏度，BLAST2使用比较低的门槛值以留下较多的高分字组，因此第3步的高分字组表会变的比较长。接著，如果在图3中以X代表的匹配字组是在同一个从左下往右上的对角线上，而且它们的距离是小于一个门槛值A，则这两个匹配的位置会被结合成一个更长的区域。最后，这个新的区域会用旧版BLAST向左右扩展的方式来延伸成HSP，而这个HSP的分数一样也是用得分矩阵来评分每一个比对的情形，并将这些分数加总起来，就跟之前找高分字组的方法一样。

     

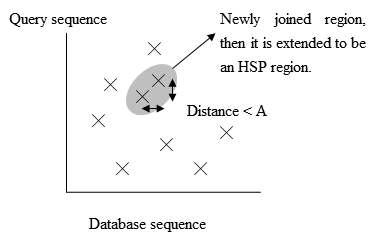
     图3.匹配字组在以Query序列和资料库序列所构成的平面上的位置

8. 将所有分数够高的HSP列出来
   所有分数高于某个由经验法则推测出来的门槛值S之HSP都将被列出。这个门槛值S是由检视两个不相关的序列去作大量无间隙的区域排比得来的分数之分布，进而推测出S该怎么制定以保证被留下来的HSP都具有一定程度的意义。
9. 评估这些留下来的HSP它们的分数是否具有意义
   BLAST会利用Gumbel extreme value distribution (EVD)（页面存档备份，存于互联网档案馆）这个极值的分布，来评估每个HSP分数的统计意义（已经有人证明两个不相关的序列去作区域排比时，不考虑gap的使用，做出来的分数都会呈现Gumbel EVD的情况；考虑gap的使用时，该结论尚未被证明）。根据Gumbel EVD所推测出来的理论，一个分数S大于或等于Gumbel EVD里面某个值x的机率是
   $p\left(S\geq x\right)=1-\exp \left(-e^{-\lambda \left(x-\mu \right)}\right)$
   ，其中
   $\mu ={}^{\left[\log \left(Km'n'\right)\right]}\!\!\diagup \!\!{}_{\lambda }\;$
   统计变数$\lambda$和$\mathrm {K}$是由Query序列去和大量被混乱排列（Globeal or local shuffling）的一个资料库序列作无间隙区域排比所形成的Gumbel EVD，再由这个来评估出这些统计变数。统计变数$\lambda$和$\mathrm {K}$取决于所使用的得分矩阵以及间隙惩罚值（Gap penalties），还有序列的元素组成成份。至于m’和n’则分别是Query序列和资料库序列的有效长度（Effective length）。有效长度的由来是因为在两序列的排比中，如果排比的起点靠近其中一个序列的结尾处时，则这个排比很难有机会形成一个好的排比，这称为边际效应（[Edge effect http://www.ncbi.nlm.nih.gov/BLAST/tutorial/Altschul-1.html#head7（页面存档备份，存于互联网档案馆）]）。因此，要利用将原始序列的长度经过一些修剪来弥补边际效应，以达到比较好的统计估测（注意，当序列的长度都大于200时，边际效应通常可被忽略）。被修正过得长度是
   $m'\approx m-{\frac {\left(\ln {\mathrm {K} mn}\right)}{\mathrm {H} }}$
   $n'\approx n-{\frac {\left(\ln {\mathrm {K} mn}\right)}{\mathrm {H} }}$（注意n是所有资料库中序列长度的总和）,
   其中$\mathrm {H}$是指两个不相关的序列去作无间隙区域排比后，每一个排比对平均所得的分数，这和我们所使用的得分矩阵密切相关。Altschul和Gish先生提供了我们这些统计变数的参考值，如$\lambda =0.318$、$\mathrm {K} =0.13$、及$\mathrm {H} =0.40$，这边使用的得分矩阵是BLOSUM62（页面存档备份，存于互联网档案馆）。使用这些参考值去作统计意义的估测其实不是非常准确。经由以上分析，我们可能找出一个和Query序列相关的资料库序列，接著我们要计算这个资料库序列的期望分数E（Expect score），它的意义是当我们对非常多个不相关序列其中的两个作无间隙区域排比时，所得的分数会高于这个资料库序列和Query序列之间的HSP分数之个数。经由搜寻一个有D个序列的资料库所得之期望分数E可由下式得到。
   $\mathrm {E} \approx 1-e^{-\mathbf {p} \left(\mathbf {S} \geq \mathbf {x} \right)}$
   甚至当$\mathbf {p} <0.1$时，E可以由泊松分布更进一步简化为
   $\mathrm {E} =\mathbf {p} \mathrm {D}$
   注意这边用来估测HSP分数（无间隙）的期望分数E和最后一个步骤用来估测具有间隙的区域排比分数的期望分数E是不一样的。差别就在是否具有间隙（Gap），所以先前的统计变数都要重新计算。
10. 将一个资料库序列中的多个HSP区域结合成一个更长的排比
    有时，我们会在一个资料库序列中找到多个HSP区域，然后将它们结合成一个更长的排比序列，这提供Query序列和资料库序列之间相关性的另一个证据。当我们要比较这些结合后的区域之间孰轻孰重时，有两种方法让我们选择。一种叫做Poisson法则（Poisson method），另外一种叫做总分法则（sum-of scores method）。假设有两个新结合出来的区域，它们个别的HSP分数分别是（65, 40）和（52, 45）。Poisson法则是以谁的低分比较高来给予评价，像（52, 45）就比（65, 40）重要，因为45>40；然而，总分法则就比较重视（65, 40）这组，因为65+40（105）比52+45（97）大。旧版的BLAST是用Poisson法则，而新版的BLAST或是WU-BLAST（页面存档备份，存于互联网档案馆）则是使用总分法则。
11. 
    显示Query序列和所有之前找到可能相关的资料库序列之有间隙区域排比
    • 旧版的BLAST只能显示出Query序列和之前找到的HSP区域之间的无间隙区域排比，甚至当一个资料库序列中有多个HSP也是一样，只会分开显示。
    • 新版的BLAST就不像旧版那样，若一个资料库序列中有多个HSP，则它可以将这些HSP统统包含进一个较大型的有间隙区域排比。这边再提醒一次，这里做出来的有间隙区域排比之分数也是用先前提到的Gumbel EVD找出的期望分数E来作评估，但这边的统计变数要考量到间隙惩罚值，因此和之前的期望分数E是不一样的。
12. 列出上一步骤中期望分数E低于我们所要求的门槛值之资料库序列

相关的各种程式

由NCBI管理的BLAST网站允许任何人使用浏览器来在包含大部分新测序的物种的不停更新的DNA或蛋白质数据库中进行相似性搜索。这个服务器包含很多程序，最重要的几个如下：

蛋白-蛋白BLAST（blastp）

已知一个蛋白的氨基酸序列，通过这个程序可以找出在用户选择的蛋白质数据库中与其最相似的序列。

已转录序列-蛋白BLAST（blastx）

已知一段已经转录的序列，借由这个程式对这段序列的6个ORF对上用户所选择的蛋白质资料库， 比对最相似的序列。其功用可以找出在基因体DNA（genomic DNA）上转译出蛋白质的序列。

蛋白-已转录序列BLAST（tblastn）

已知一段蛋白质的氨基酸序列，借由这个程式可将此序列，对用户所选择的已转录序列资料库（包含这个资料库的6个ORF），比对出最相似的序列。

已转录序列-已转录序列BLAST（tblastx）

已知一段已转录的序列，借由这个程式对这已知序列的6个ORF，对上用户所选择的已转录序列资料库（亦包含6个ORF），比对出最相似的序列，因为这个程式比对来源的6个ORF，与资料库的6个ORF，所以会执行相当久。

位置相关的迭代BLAST（PSI-BLAST）

这个程序用来搜索蛋白质的"远亲".首先，一个用户提交的蛋白质序列的所有"近亲"的列表被建立起来，然后这些蛋白质被结合在一个作为对序列的某种平均的"特征序列"当中。再然后用这个特征序列在蛋白质数据库中进行搜索，就会找出更大的一组蛋白质的列表。这个蛋白质列表有一个不同的特征序列，这个序列被用来迭代地运行上述过程。

通过在搜索中包含相关的蛋白质，PSI-BLAST对于寻找已知蛋白进化上的"远亲"的灵敏度要比一般的blastp高很多。

PHI-BLAST

Focuses search around pattern (motif)

外部链接

• NCBI-BLAST 首页（页面存档备份，存于互联网档案馆）
• NCBI-BLAST 教程（页面存档备份，存于互联网档案馆）

参见

• 序列比对