此條目需要
精通或熟悉相關主題的編者 參與及協助編輯。
(2015年1月23日 ) 請邀請 適合的人士改善本條目 。更多的細節與詳情請參見討論頁 。
在應用數學的分析方面,剪切小波 (英語:Shearlet )是一個多尺度的架構,且在多變量問題中能高效率編碼有各向異性 的特點。起初,為了分析及稀疏近似多維方程式
f
∈
L
2
(
R
2
)
{\displaystyle f\in L^{2}(\mathbb {R} ^{2})}
[ 1] 小波分析 的自然延伸,可以適應有各向異性特點的多元方程式,像是影像的輪廓、邊緣。然而,各向同性的小波是不能得到此現象。
把拋物線的縮放 、剪切、平移 施加在數個生成函數後可建構出剪切小波。雖然所建構出的剪切小波不能建構出在空間
L
2
(
R
2
)
{\displaystyle L^{2}(\mathbb {R} ^{2})}
正交基底 ,它們仍然可以形成一個架構
剪切小波具有以下幾個重要性質:
良好的局部性。它在空間中具有快速的衰減性,在頻域內是緊支撐的。
靈敏的方向性。通過一個剪切矩陣來控制方向,隨著尺度逐漸精細化,其方向性也會逐漸變得更靈敏。
良好的稀疏逼近性。其逼近率與曲波變換 和輪廓波變換
C
N
−
2
(
log
N
)
3
{\displaystyle CN^{-2}(\log N)^{3}}
[ 2] [ 3]
C
{\displaystyle C}
f
{\displaystyle f}
f
′
{\displaystyle f^{'}}
f
″
{\displaystyle f^{''}}
O
(
N
−
1
)
{\displaystyle O(N^{-1})}
N
{\displaystyle N}
多方辨性。它是由一個或一組函數的縮放平移生成的一個仿射系統,能設計出快速分解重設法。
一致性。能一致處理連續和離散的情況,剪切小波不僅克服了輪廓波和典型小波的不足,也繼承了它們的優點。它既能接近最佳的表示一類高維函數,如類卡通圖像[ 4] 剪切小波是迄今為止唯一有方向性且提供各向異性特點的稀疏估計的表現系統,可擴展至
L
2
(
R
d
)
,
d
≥
2
{\displaystyle L^{2}(\mathbb {R} ^{d}),d\geq 2}
[ 5]
拋物線縮放和剪切的幾何效果,使用一些不同參數a和 s.
連續剪切小波系統的架構是基於拋物線縮放矩陣
A
a
=
[
a
0
0
a
1
/
2
]
,
a
>
0
{\displaystyle A_{a}={\begin{bmatrix}a&0\\0&a^{1/2}\end{bmatrix}},\quad a>0}
為一個改變解析度的方法。剪切矩陣
S
s
=
[
1
s
0
1
]
,
s
∈
R
{\displaystyle S_{s}={\begin{bmatrix}1&s\\0&1\end{bmatrix}},\quad s\in \mathbb {R} }
為一個改變方向的方法。最後再用平移去改變位置。相較於曲波變換,剪切小波利用剪切的方法取代旋轉的方法,其優點在於如果
s
∈
Z
{\displaystyle s\in \mathbb {Z} }
S
s
{\displaystyle S_{s}}
s
∈
Z
{\displaystyle s\in \mathbb {Z} }
x
=
[
x
y
]
,
x
,
y
∈
Z
{\displaystyle \mathbf {x} ={\begin{bmatrix}x\\y\end{bmatrix}},x,y\in \mathbb {Z} }
S
s
x
=
[
x
−
s
y
y
]
∈
Z
2
{\displaystyle S_{s}\mathbf {x} ={\begin{bmatrix}x-sy\\y\end{bmatrix}}\in \mathbb {Z} ^{2}}
結果依然在整數採樣點上。[ 5]
給定一個
ψ
∈
L
2
(
R
2
)
{\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})}
ψ
∈
L
2
(
R
2
)
{\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})}
SH
c
o
n
t
(
ψ
)
=
{
ψ
a
,
s
,
t
=
a
3
/
4
ψ
(
S
s
A
a
(
⋅
−
t
)
)
∣
a
>
0
,
s
∈
R
,
t
∈
R
2
}
,
{\displaystyle \operatorname {SH} _{\mathrm {cont} }(\psi )=\{\psi _{a,s,t}=a^{3/4}\psi (S_{s}A_{a}(\cdot -t))\mid a>0,s\in \mathbb {R} ,t\in \mathbb {R} ^{2}\},}
其對應的連續剪切小波轉換:
f
↦
S
H
ψ
f
(
a
,
s
,
t
)
=
⟨
f
,
ψ
a
,
s
,
t
⟩
,
f
∈
L
2
(
R
2
)
,
(
a
,
s
,
t
)
∈
R
>
0
×
R
×
R
2
.
{\displaystyle f\mapsto {\mathcal {SH}}_{\psi }f(a,s,t)=\langle f,\psi _{a,s,t}\rangle ,\quad f\in L^{2}(\mathbb {R} ^{2}),\quad (a,s,t)\in \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}
離散的剪切小波系統可以直接從
SH
c
o
n
t
(
ψ
)
{\displaystyle \operatorname {SH} _{\mathrm {cont} }(\psi )}
R
>
0
×
R
×
R
2
.
{\displaystyle \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}
{
(
2
j
,
k
,
A
2
j
−
1
S
k
−
1
m
)
∣
j
∈
Z
,
k
∈
Z
,
m
∈
Z
2
}
⊆
R
>
0
×
R
×
R
2
.
{\displaystyle \{(2^{j},k,A_{2^{j}}^{-1}S_{k}^{-1}m)\mid j\in \mathbb {Z} ,k\in \mathbb {Z} ,m\in \mathbb {Z} ^{2}\}\subseteq \mathbb {R} _{>0}\times \mathbb {R} \times \mathbb {R} ^{2}.}
從這個式子,與剪切運算子有關的離散剪切小波系統被定義為:
SH
(
ψ
)
=
{
ψ
j
,
k
,
m
=
2
3
j
/
4
ψ
(
S
k
A
2
j
⋅
−
m
)
∣
j
∈
Z
,
k
∈
Z
,
m
∈
Z
2
}
,
{\displaystyle \operatorname {SH} (\psi )=\{\psi _{j,k,m}=2^{3j/4}\psi (S_{k}A_{2^{j}}\cdot {}-m)\mid j\in \mathbb {Z} ,k\in \mathbb {Z} ,m\in \mathbb {Z} ^{2}\},}
其相關的離散剪切小波轉換被定義為:
f
↦
S
H
ψ
f
(
j
,
k
,
m
)
=
⟨
f
,
ψ
j
,
k
,
m
⟩
,
f
∈
L
2
(
R
2
)
,
(
j
,
k
,
m
)
∈
Z
×
Z
×
Z
2
.
{\displaystyle f\mapsto {\mathcal {SH}}_{\psi }f(j,k,m)=\langle f,\psi _{j,k,m}\rangle ,\quad f\in L^{2}(\mathbb {R} ^{2}),\quad (j,k,m)\in \mathbb {Z} \times \mathbb {Z} \times \mathbb {Z} ^{2}.}
設
ψ
1
∈
L
2
(
R
)
{\displaystyle \psi _{1}\in L^{2}(\mathbb {R} )}
∑
j
∈
Z
|
ψ
^
1
(
2
−
j
ξ
)
|
2
=
1
,
for a.e.
ξ
∈
R
,
{\displaystyle \sum _{j\in \mathbb {Z} }|{\hat {\psi }}_{1}(2^{-j}\xi )|^{2}=1,{\text{for a.e. }}\xi \in \mathbb {R} ,}
ψ
^
1
∈
C
∞
(
R
)
{\displaystyle {\hat {\psi }}_{1}\in C^{\infty }(\mathbb {R} )}
supp
ψ
^
1
⊆
[
−
1
2
,
−
1
16
]
∪
[
1
16
,
1
2
]
{\displaystyle \operatorname {supp} {\hat {\psi }}_{1}\subseteq [-{\tfrac {1}{2}},-{\tfrac {1}{16}}]\cup [{\tfrac {1}{16}},{\tfrac {1}{2}}]}
ψ
^
1
{\displaystyle {\hat {\psi }}_{1}}
ψ
1
{\displaystyle \psi _{1}}
傅立葉變換 。例如,可以選擇
ψ
1
{\displaystyle \psi _{1}}
ψ
2
∈
L
2
(
R
)
{\displaystyle \psi _{2}\in L^{2}(\mathbb {R} )}
ψ
^
2
∈
C
∞
(
R
)
,
{\displaystyle {\hat {\psi }}_{2}\in C^{\infty }(\mathbb {R} ),}
supp
ψ
^
2
⊆
[
−
1
,
1
]
{\displaystyle \operatorname {supp} {\hat {\psi }}_{2}\subseteq [-1,1]}
∑
k
=
−
1
1
|
ψ
^
2
(
ξ
+
k
)
|
2
=
1
,
for a.e.
ξ
∈
[
−
1
,
1
]
.
{\displaystyle \sum _{k=-1}^{1}|{\hat {\psi }}_{2}(\xi +k)|^{2}=1,{\text{for a.e. }}\xi \in \left[-1,1\right].}
通常會選擇一個沖擊函數 作為
ψ
^
2
{\displaystyle {\hat {\psi }}_{2}}
ψ
∈
L
2
(
R
2
)
{\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})}
ψ
^
(
ξ
)
=
ψ
^
1
(
ξ
1
)
ψ
^
2
(
ξ
2
ξ
1
)
,
ξ
=
(
ξ
1
,
ξ
2
)
∈
R
2
,
{\displaystyle {\hat {\psi }}(\xi )={\hat {\psi }}_{1}(\xi _{1}){\hat {\psi }}_{2}\left({\tfrac {\xi _{2}}{\xi _{1}}}\right),\quad \xi =(\xi _{1},\xi _{2})\in \mathbb {R} ^{2},}
這被稱作一個典型的剪切小波。其對應的離散剪切小波系統
SH
(
ψ
)
{\displaystyle \operatorname {SH} (\psi )}
L
2
(
R
2
)
{\displaystyle L^{2}(\mathbb {R} ^{2})}
[ 5]
另外一個例子是緊支撐的剪切小波系統,其中要選定緊支撐函數
ψ
∈
L
2
(
R
2
)
{\displaystyle \psi \in L^{2}(\mathbb {R} ^{2})}
SH
(
ψ
)
{\displaystyle \operatorname {SH} (\psi )}
L
2
(
R
2
)
{\displaystyle L^{2}(\mathbb {R} ^{2})}
[ 3] [ 6] [ 7] [ 8]
SH
(
ψ
)
{\displaystyle \operatorname {SH} (\psi )}
f
∈
L
2
(
R
2
)
{\displaystyle f\in L^{2}(\mathbb {R} ^{2})}
上述所定義的剪切小波有其缺陷,那就是剪切小波元素的方向性偏差與大的剪切參數有關聯。在典型剪切小波的頻率拼接(在#範例 中的圖可見)中可以看到這個影響,當剪切參數
s
{\displaystyle s}
ξ
2
{\displaystyle \xi _{2}}
ξ
2
{\displaystyle \xi _{2}}
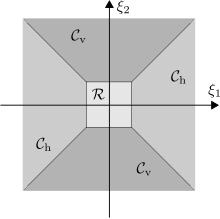
將頻域分解成錐形和低頻區域 為了解決這個問題,頻域被分成一個低頻部分和兩個錐形部分(如圖所示):
R
=
{
(
ξ
1
,
ξ
2
)
∈
R
2
∣
|
ξ
1
|
,
|
ξ
2
|
≤
1
}
,
C
h
=
{
(
ξ
1
,
ξ
2
)
∈
R
2
∣
|
ξ
2
/
ξ
1
|
≤
1
,
|
ξ
1
|
>
1
}
,
C
v
=
{
(
ξ
1
,
ξ
2
)
∈
R
2
∣
|
ξ
1
/
ξ
2
|
≤
1
,
|
ξ
2
|
>
1
}
.
{\displaystyle {\begin{aligned}{\mathcal {R}}&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{1}|,|\xi _{2}|\leq 1\right\},\\{\mathcal {C}}_{\mathrm {h} }&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{2}/\xi _{1}|\leq 1,|\xi _{1}|>1\right\},\\{\mathcal {C}}_{\mathrm {v} }&=\left\{(\xi _{1},\xi _{2})\in \mathbb {R} ^{2}\mid |\xi _{1}/\xi _{2}|\leq 1,|\xi _{2}|>1\right\}.\end{aligned}}}
由典型剪切小波生成的自適應性剪切小波系統的頻率拼接 這個自適應性剪切小波系統是由三個部分組成,每個部分都對應到這些頻域之一,這個系統是由三個函數
ϕ
,
ψ
,
ψ
~
∈
L
2
(
R
2
)
{\displaystyle \phi ,\psi ,{\tilde {\psi }}\in L^{2}(\mathbb {R} ^{2})}
c
=
(
c
1
,
c
2
)
∈
(
R
>
0
)
2
{\displaystyle c=(c_{1},c_{2})\in (\mathbb {R} _{>0})^{2}}
SH
(
ϕ
,
ψ
,
ψ
~
;
c
)
=
Φ
(
ϕ
;
c
1
)
∪
Ψ
(
ψ
;
c
)
∪
Ψ
~
(
ψ
~
;
c
)
,
{\displaystyle \operatorname {SH} (\phi ,\psi ,{\tilde {\psi }};c)=\Phi (\phi ;c_{1})\cup \Psi (\psi ;c)\cup {\tilde {\Psi }}({\tilde {\psi }};c),}
其中:
Φ
(
ϕ
;
c
1
)
=
{
ϕ
m
=
ϕ
(
⋅
−
c
1
m
)
∣
m
∈
Z
2
}
,
Ψ
(
ψ
;
c
)
=
{
ψ
j
,
k
,
m
=
2
3
j
/
4
ψ
(
S
k
A
2
j
⋅
−
M
c
m
)
∣
j
≥
0
,
|
k
|
≤
⌈
2
j
/
2
⌉
,
m
∈
Z
2
}
,
Ψ
~
(
ψ
~
;
c
)
=
{
ψ
~
j
,
k
,
m
=
2
3
j
/
4
ψ
(
S
~
k
A
~
2
j
⋅
−
M
~
c
m
)
∣
j
≥
0
,
|
k
|
≤
⌈
2
j
/
2
⌉
,
m
∈
Z
2
}
,
{\displaystyle {\begin{aligned}\Phi (\phi ;c_{1})&=\{\phi _{m}=\phi (\cdot {}-c_{1}m)\mid m\in \mathbb {Z} ^{2}\},\\\Psi (\psi ;c)&=\{\psi _{j,k,m}=2^{3j/4}\psi (S_{k}A_{2^{j}}\cdot {}-M_{c}m)\mid j\geq 0,|k|\leq \lceil 2^{j/2}\rceil ,m\in \mathbb {Z} ^{2}\},\\{\tilde {\Psi }}({\tilde {\psi }};c)&=\{{\tilde {\psi }}_{j,k,m}=2^{3j/4}\psi ({\tilde {S}}_{k}{\tilde {A}}_{2^{j}}\cdot {}-{\tilde {M}}_{c}m)\mid j\geq 0,|k|\leq \lceil 2^{j/2}\rceil ,m\in \mathbb {Z} ^{2}\},\end{aligned}}}
式子中的一些變數定義如下;
A
~
a
=
[
a
1
/
2
0
0
a
]
,
a
>
0
,
S
~
s
=
[
1
0
s
1
]
,
s
∈
R
,
M
c
=
[
c
1
0
0
c
2
]
,
and
M
~
c
=
[
c
2
0
0
c
1
]
.
{\displaystyle {\begin{aligned}&{\tilde {A}}_{a}={\begin{bmatrix}a^{1/2}&0\\0&a\end{bmatrix}},\;a>0,\quad {\tilde {S}}_{s}={\begin{bmatrix}1&0\\s&1\end{bmatrix}},\;s\in \mathbb {R} ,\quad M_{c}={\begin{bmatrix}c_{1}&0\\0&c_{2}\end{bmatrix}},\quad {\text{and}}\quad {\tilde {M}}_{c}={\begin{bmatrix}c_{2}&0\\0&c_{1}\end{bmatrix}}.\end{aligned}}}
系統
Ψ
(
ψ
)
{\displaystyle \Psi (\psi )}
Ψ
~
(
ψ
~
)
{\displaystyle {\tilde {\Psi }}({\tilde {\psi }})}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
C
h
{\displaystyle {\mathcal {C}}_{\mathrm {h} }}
C
v
{\displaystyle {\mathcal {C}}_{\mathrm {v} }}
ϕ
{\displaystyle \phi }
R
{\displaystyle {\mathcal {R}}}
^ Guo, Kanghui, Gitta Kutyniok, and Demetrio Labate. "Sparse multidimensional representations using anisotropic dilation and shear operators." Wavelets and Splines (Athens, GA, 2005), G. Chen and MJ Lai, eds., Nashboro Press, Nashville, TN (2006): 189–201.
PDF PDF
^ Guo, Kanghui, and Demetrio Labate. "Optimally sparse multidimensional representation using shearlets." SIAM Journal on Mathematical Analysis 39.1 (2007): 298–318.
PDF PDF
^ 3.0 3.1 Kutyniok, Gitta, and Wang-Q Lim. "Compactly supported shearlets are optimally sparse." Journal of Approximation Theory 163.11 (2011): 1564–1589.
PDF PDF
^ Donoho, David Leigh. "Sparse components of images and optimal atomic decompositions." Constructive Approximation 17.3 (2001): 353–382.
PDF PDF
^ 5.0 5.1 5.2 5.3 5.4 Kutyniok, Gitta, and Demetrio Labate, eds. Shearlets: Multiscale analysis for multivariate data . Springer, 2012, ISBN 0-8176-8315-1
^ Kittipoom, Pisamai, Gitta Kutyniok, and Wang-Q Lim. "Construction of compactly supported shearlet frames." Constructive Approximation 35.1 (2012): 21–72.
PDF PDF
^ Kutyniok, Gitta, Jakob Lemvig, and Wang-Q Lim. "Optimally sparse approximations of 3D functions by compactly supported shearlet frames." SIAM Journal on Mathematical Analysis 44.4 (2012): 2962–3017.
PDF PDF
^ Purnendu Banerjee and B. B. Chaudhuri, 「Video Text Localization using Wavelet and Shearlet Transforms」, In Proc. SPIE 9021, Document Recognition and Retrieval XXI, 2014 (doi:10.1117/12.2036077).PDF PDF
































![{\displaystyle \operatorname {supp} {\hat {\psi }}_{1}\subseteq [-{\tfrac {1}{2}},-{\tfrac {1}{16}}]\cup [{\tfrac {1}{16}},{\tfrac {1}{2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9781e9cfcce51978a270b8e09fc4b00106a90cc)




![{\displaystyle \operatorname {supp} {\hat {\psi }}_{2}\subseteq [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be9d7048ed3022be72a06f098288a848f9feef6)
![{\displaystyle \sum _{k=-1}^{1}|{\hat {\psi }}_{2}(\xi +k)|^{2}=1,{\text{for a.e. }}\xi \in \left[-1,1\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fa08b5c6527adfc7cc1f2651b4b413109730f1e)


















