加性高斯白噪聲

加性高斯白噪聲（英語：Additive white Gaussian noise，AWGN）在通信領域中指的是一種功率譜函數是常數（即白噪聲），且幅度服從高斯分布的噪聲信號。因其可加性、幅度服從高斯分布且為白噪聲的一種而得名。

該噪聲信號為一種便於分析的理想噪聲信號，實際的噪聲信號往往只在某一頻段內可以用高斯白噪聲的特性來進行近似處理。由於AWGN信號易於分析、近似，因此在信號處理領域，對信號處理系統（如濾波器、低噪音高頻放大器、無線信號傳輸等）的噪聲性能的簡單分析(如：信噪比分析)中，一般可假設系統所產生的噪音或受到的噪音信號干擾在某頻段或限制條件之下是高斯白噪聲。

加性高斯白噪聲只是白噪聲的一種，另有泊松白噪聲等。

信道容量

AWGN 信道由一系列的$Y_{i}$（輸出） 來表示，其中的 $i$ 表示離散的時間事件索引。$Y_{i}$ 是 $X_{i}$（輸入）和$Z_{i}$（噪聲）的數值和，其中 $Z_{i}$ 是獨立恆等分布的隨機變量並來自於均值為 0，方差為 $N$（噪聲） 的正態分布。$Z_{i}$ 可以進一步認為和 $X_{i}$ 有關。

$Z_{i}\sim {\mathcal {N}}(0,N)\,\!$

$Y_{i}=X_{i}+Z_{i}\,\!$

信道的容量是無窮的，除非噪聲 $n$ 非零且 $X_{i}$ 有足夠的約束。輸入中最常見的約束被叫做功率約束，這要求碼字$(x_{1},x_{2},\dots ,x_{k})$ 通過信道傳送。我們有：

${\frac {1}{k}}\sum _{i=1}^{k}x_{i}^{2}\leq P,\,\!$

其中 $P$ 代表信道功率的最大值。因此信道容量的功率約束可以通過以下公式給出：

$C=\max _{f(x){\text{ s.t. }}E\left(X^{2}\right)\leq P}I(X;Y)\,\!$

這裡，$f(x)$ 是 $X$ 的分布。$I(X;Y)$ 可以擴展為微分熵的形式：

${\begin{aligned}I(X;Y)=h(Y)-h(Y|X)&=h(Y)-h(X+Z|X)&=h(Y)-h(Z|X)\end{aligned}}\,\!$

但是 $X$ 和 $Z$ 是獨立的，因此：

$I(X;Y)=h(Y)-h(Z)\,\!$

通過計算高斯微分熵可給出：

$h(Z)={\frac {1}{2}}\log(2\pi eN)\,\!$

因為 $X$ 和 $Z$ 是獨立的並且它們的和給出了 $Y$：

$E(Y^{2})=E(X+Z)^{2}=E(X^{2})+2E(X)E(Z)+E(Z^{2})=P+N\,\!$

從此約束中，我們可以從微分熵的屬性中推斷出：

$h(Y)\leq {\frac {1}{2}}\log(2\pi e(P+N))\,\!$

因此通道容量可以通過可變信息中的最高可獲取約束求得：

$I(X;Y)\leq {\frac {1}{2}}\log(2\pi e(P+N))-{\frac {1}{2}}\log(2\pi eN)\,\!$

其中 $I(X;Y)$ 在

$X\sim {\mathcal {N}}(0,P)\,\!$

時最大。

因此 AWGN 的信道容量 $C$可以由此給出：

$C={\frac {1}{2}}\log \left(1+{\frac {P}{N}}\right)\,\!$

時域中的影響

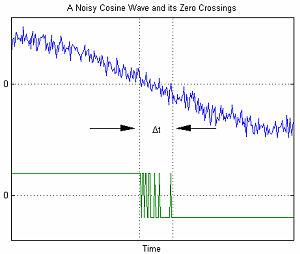Zero-Crossings of a Noisy Cosine

在串行數據通信中，AWGN 數學模型被用來對由隨機抖動引發的時間性錯誤建模。

右圖中展示了和 AWGN 關聯的時間性錯誤。變量 $\Delta t$ 表示零點交叉處的不確定性。當 AWGN 中的振幅被提升時，信噪比降低。這導致不確定性 $\Delta t$ 降低。

當受 AWGN 影響時。當輸入是一個正弦波時，窄通頻帶濾波輸出中的每一秒，不管是正向趨近於零點交叉還是負趨向於零點交叉的平均數都是：

${\frac {\mathrm {positive\ zero\ crossings} }{\mathrm {second} }}={\frac {\mathrm {negative\ zero\ crossings} }{\mathrm {second} }}$

$=f_{0}{\sqrt {\frac {\mathrm {SNR} +1+{\frac {B^{2}}{12f_{0}^{2}}}}{\mathrm {SNR} +1}}}$

其中

• f₀ = 濾波的中心頻率
• B = 濾波器帶寬
• SNR = 線性關係上的信噪功率比

相域中的影響

在現代通信系統中，帶寬受限的AWGN(加性高斯白噪聲)不容忽視。統計分析表明，對相量域中帶寬受限的AWGN調製時，實部和虛部的振幅是遵循高斯分布模型的相互獨立的變量。組合後，所產生的相量是符合瑞利分布的隨機變量，而其相位從0到2π均勻分布。

參照

• 接地反彈
• 有噪信道編碼定理
• 高斯過程