本文只考慮歐幾里得空間中的曲線。大部分概念對
黎曼 與
偽黎曼 流形 中曲線有類似結論。對任意
空間 中曲線的討論,參見主條目
曲線 。
曲線的微分幾何 是幾何學 的一個分支,使用微分 與積分 專門研究平面 與歐幾里得空間 中的光滑 曲線 。
從古代開始,許多具體曲線 已經用綜合方法深入研究。微分幾何 採取另外一種方式:把曲線表示為參數形式 ,將它們的幾何性質和各種量,比如曲率 和弧長 ,用向量分析 表示為導數 和積分 。分析曲線最重要的工具之一為 Frenet 標架 ,是一個活動標架 ,在曲線每一點附近給出「最合適」的坐標系。
曲線的理論比曲面理論 及其高維推廣的範圍要狹窄得多,也簡單得多。因為歐幾里得空間中的正則曲線沒有內蘊幾何。任何正則曲線可以用弧長(「自然參數」)參數化,從曲線上來看不能知道周圍空間的任何信息,所有曲線都是一樣的。不同空間曲線只是由它們的彎曲和扭曲程度區分。數量上,這由微分幾何不變量曲線的「曲率 」和「撓率 」來衡量。曲線基本定理 斷言這些不變量的信息完全確定了曲線。
設
n
{\displaystyle n}
r
{\displaystyle r}
∞
{\displaystyle \infty }
I
{\displaystyle I}
非空 區間,
t
{\displaystyle t}
I
{\displaystyle I}
C
r
{\displaystyle C^{r}}
γ
{\displaystyle \gamma }
r
{\displaystyle r}
連續可微 )向量值函數
γ
:
I
→
R
n
{\displaystyle \mathbf {\gamma } :I\to {\mathbb {R} }^{n}}
稱為一條
C
r
{\displaystyle C^{r}}
γ
{\displaystyle \gamma }
C
r
{\displaystyle C^{r}}
t
{\displaystyle t}
γ
{\displaystyle \gamma }
γ
(
I
)
{\displaystyle \gamma (I)}
像 。將參數曲線
γ
{\displaystyle \gamma }
γ
(
I
)
{\displaystyle \gamma (I)}
R
n
{\displaystyle {\mathbb {R} }^{n}}
可以想象參數
t
{\displaystyle t}
γ
(
t
)
{\displaystyle \gamma (t)}
軌跡 。
如果 I 是閉區間 [a , b ],我們稱 γ(a ) 為曲線 γ 的起點 而 γ(b ) 為終點 。
如果
γ
(
a
)
=
γ
(
b
)
{\displaystyle \gamma (a)=\gamma (b)}
閉的 或是一個環路 。進一步,我們稱 γ 是一條閉 Cr -曲線 ,如果 γ(k ) (a) = γ(k ) (b ) 對所有 k ≤ r 。
如果
γ
:
(
a
,
b
)
→
R
n
{\displaystyle \gamma :(a,b)\to \mathbb {R} ^{n}}
單射 ,我們稱為簡單 曲線。
如果參數曲線
γ
{\displaystyle \gamma }
冪級數 ,我們稱曲線解析 或是
C
ω
{\displaystyle C^{\omega }}
記號 -
γ
{\displaystyle \gamma }
一條
C
k
{\displaystyle C^{k}}
γ
:
[
a
,
b
]
→
R
n
{\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}
稱為
m
{\displaystyle m}
當且僅當 對任何
t
{\displaystyle t}
I
{\displaystyle I}
{
γ
′
(
t
)
,
γ
″
(
t
)
,
.
.
.
,
γ
(
m
)
(
t
)
}
,
m
≤
k
{\displaystyle \lbrace \gamma '(t),\gamma ''(t),...,\gamma ^{(m)}(t)\rbrace {\mbox{, }}m\leq k}
在
R
n
{\displaystyle \mathbb {R} ^{n}}
線性無關 。
特別地,一條
C
1
{\displaystyle C^{1}}
γ
{\displaystyle \gamma }
正則 的如果
γ
′
(
t
)
≠
0
{\displaystyle \gamma '(t)\neq 0}
t
∈
I
.
{\displaystyle t\in I\,.}
給定一條曲線的像我們可以定義曲線的許多不同的參數化。微分幾何旨在描述在一定的參數化下不變的性質。所以我們需在所有參數曲線集合上定義一種合適的等價關係 。曲線的微分幾何性質(長度,Frenet 標架 和廣義曲率)在重新參數化下不變從而滿足等價類 性質。這個等價類稱為 Cr 曲線 ,是曲線的微分幾何研究的中心。
兩個 C r
γ
1
:
I
1
→
R
n
{\displaystyle \mathbf {\gamma _{1}} :I_{1}\to R^{n}}
與
γ
2
:
I
2
→
R
n
{\displaystyle \mathbf {\gamma _{2}} :I_{2}\to R^{n}}
要稱為等價 ,就要存在一個 C r 雙射
ϕ
:
I
1
→
I
2
{\displaystyle \phi :I_{1}\to I_{2}}
使得
ϕ
′
(
t
)
≠
0
(
t
∈
I
1
)
{\displaystyle \phi '(t)\neq 0\qquad (t\in I_{1})}
和
γ
2
(
ϕ
(
t
)
)
=
γ
1
(
t
)
(
t
∈
I
1
)
.
{\displaystyle \mathbf {\gamma _{2}} (\phi (t))=\mathbf {\gamma _{1}} (t)\qquad (t\in I_{1})\,.}
γ2 稱為 γ1 的重新參數化 。這種 γ1 的重新參數化在所有參數 C r Cr 曲線 。
對定向 Cr 曲線 ,我們可以定義一種「加細」的等價關係,要求 φ 滿足 φ'(t ) > 0。
等價的 C r C r
C 1 曲線 γ : [a , b ] → R n l 可以定義為
l
=
∫
a
b
|
γ
′
(
t
)
|
d
t
.
{\displaystyle l=\int _{a}^{b}\vert \mathbf {\gamma } '(t)\vert dt.}
曲線的長度在重參數化下保持不變,從而是曲線的一個微分幾何性質。
對任何正則 C r r 至少為 1)曲線 γ: [a , b ] → R n
s
(
t
)
=
∫
t
0
t
|
γ
′
(
x
)
|
d
x
.
{\displaystyle s(t)=\int _{t_{0}}^{t}\vert \mathbf {\gamma } '(x)\vert dx.}
寫成
γ
(
s
)
¯
=
γ
(
t
(
s
)
)
{\displaystyle {\overline {\mathbf {\gamma } (s)}}=\gamma (t(s))}
這裡 t (s ) 是 s (t ) 的逆函數,我們得到 γ 的一個新參數化
γ
¯
{\displaystyle {\bar {\gamma }}}
自然 、弧長 或單位速度 參數化;參數 s (t ) 稱為 γ 的自然參數 。
我們偏愛這個參數,因為自然參數 s (t ) 以單位速度轉動 γ 的像,所以
|
γ
′
(
s
(
t
)
)
¯
|
=
1
(
t
∈
I
)
.
{\displaystyle \vert {\overline {\mathbf {\gamma } '(s(t))}}\vert =1\qquad (t\in I).}
在實際中常常很難計算出一條曲線的自然參數,但在理論討論中很有用。
給定一條參數化曲線 γ(t ) 的自然參數化是在差一個參數移動的意義下是惟一的。
數量
E
(
γ
)
=
1
2
∫
a
b
|
γ
′
(
t
)
|
2
d
t
{\displaystyle E(\gamma )={\frac {1}{2}}\int _{a}^{b}\vert \mathbf {\gamma } '(t)\vert ^{2}dt}
經常稱為曲線的能量 或作用量 ;這個名稱是有理由的,因為測地線 方程是這個作用量的歐拉-拉格朗日 運動方程。
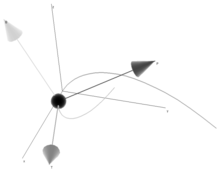
空間曲線一點的 Frenet 標架示意圖。 T 是單位切向量,P 為單位法向量,B 是次法向量。 一個 Frenet 標架 是一個移動的參考標架 ,由描述曲線在每一點 γ(t ) 局部性質的n 個正交 向量 e i t ) 組成。這是微分幾何處理曲線的主要工具,因為在這個局部參考系中,遠比使用歐幾里得那樣的整體坐標系更容易和自然地描述局部性質(如曲率、撓率)。
給定 R n n 階正則 C n +1Frenet 標架 是一組正交向量
e
1
(
t
)
,
…
,
e
n
(
t
)
{\displaystyle \mathbf {e} _{1}(t),\ldots ,\mathbf {e} _{n}(t)}
稱為 Frenet 向量 t ) 的各階導數使用格拉姆-施密特正交化算法 得到的:
e
1
(
t
)
=
γ
′
(
t
)
‖
γ
′
(
t
)
‖
{\displaystyle \mathbf {e} _{1}(t)={\frac {\mathbf {\gamma } '(t)}{\|\mathbf {\gamma } '(t)\|}}}
e
j
(
t
)
=
e
j
¯
(
t
)
‖
e
j
¯
(
t
)
‖
,
e
j
¯
(
t
)
=
γ
(
j
)
(
t
)
−
∑
i
=
1
j
−
1
⟨
γ
(
j
)
(
t
)
,
e
i
(
t
)
⟩
e
i
(
t
)
{\displaystyle \mathbf {e} _{j}(t)={\frac {{\overline {\mathbf {e} _{j}}}(t)}{\|{\overline {\mathbf {e} _{j}}}(t)\|}}{\mbox{, }}{\overline {\mathbf {e} _{j}}}(t)=\mathbf {\gamma } ^{(j)}(t)-\sum _{i=1}^{j-1}\langle \mathbf {\gamma } ^{(j)}(t),\mathbf {e} _{i}(t)\rangle \,\mathbf {e} _{i}(t)}
實值函數 χi t ) 稱為 廣義曲率 ,定義為
χ
i
(
t
)
=
⟨
e
i
′
(
t
)
,
e
i
+
1
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \chi _{i}(t)={\frac {\langle \mathbf {e} _{i}'(t),\mathbf {e} _{i+1}(t)\rangle }{\|\mathbf {\gamma } ^{'}(t)\|}}}
Frenet 標架和廣義曲率在重新參數化下是不變的,故它們是曲線的微分幾何性質。
最初三個 Frenet 向量和廣義曲率可以在三維空間中看到。它們有額外的名字以及與名稱相關更多信息。
如果曲線 γ 表示一個質點的軌跡,那麼質點在給定點 P 的瞬時速度用一個向量 表示,稱為曲線在 P 的切向量 。
數學表述為,給定一條曲線 γ = γ(t ),對參數 t 的任何值: t = t0 ,
向量:
γ
′
(
t
0
)
=
d
d
t
γ
(
t
)
,
t
=
t
0
{\displaystyle \gamma '(t_{0})={\frac {d}{d\,t}}\mathbf {\gamma } (t),{t=t_{0}}}
是點 P = γ(t0 ) 的切向量。一般說,切向量可以為零向量 。
切向量的長度:
‖
γ
′
(
t
0
)
‖
{\displaystyle \|\mathbf {\gamma } '(t_{0})\|}
是在時間 t 0 的速率。
e1 (t ) 是在同一方向的單位切向量 ,在 γ 的每個正則點有定義:
e
1
(
t
)
=
γ
′
(
t
)
‖
γ
′
(
t
)
‖
.
{\displaystyle \mathbf {e} _{1}(t)={\frac {\mathbf {\gamma } '(t)}{\|\mathbf {\gamma } '(t)\|}}.}
如果 t = s 是自然參數則切向量有單位長,從而公式化簡為:
e
1
(
s
)
=
γ
′
(
s
)
.
{\displaystyle \mathbf {e} _{1}(s)=\mathbf {\gamma } '(s).}
單位切向量確定了曲線的定向 ,或隨著參數增長的前進方向。
法向量 ,有時也稱為曲率向量 ,表明曲線和一條直線的偏離程度。
法向量定義為
e
2
¯
(
t
)
=
γ
″
(
t
)
−
⟨
γ
″
(
t
)
,
e
1
(
t
)
⟩
e
1
(
t
)
.
{\displaystyle {\overline {\mathbf {e} _{2}}}(t)=\mathbf {\gamma } ''(t)-\langle \mathbf {\gamma } ''(t),\mathbf {e} _{1}(t)\rangle \,\mathbf {e} _{1}(t).}
其正規形式單位法向量 ,是 Frenet 向量 e 2 (t ),定義為
e
2
(
t
)
=
e
2
¯
(
t
)
‖
e
2
¯
(
t
)
‖
.
{\displaystyle \mathbf {e} _{2}(t)={\frac {{\overline {\mathbf {e} _{2}}}(t)}{\|{\overline {\mathbf {e} _{2}}}(t)\|}}.}
t 點的切向量和法向量張成 t 點的密切平面 。
第一個廣義曲率 χ1 (t ) 稱為曲率 ,度量了曲線 γ 偏離密切平面上一條直線的程度。定義為
κ
(
t
)
=
χ
1
(
t
)
=
⟨
e
1
′
(
t
)
,
e
2
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \kappa (t)=\chi _{1}(t)={\frac {\langle \mathbf {e} _{1}'(t),\mathbf {e} _{2}(t)\rangle }{\|\mathbf {\gamma } ^{'}(t)\|}}}
稱為 γ 在點 t 的曲率 。
曲率的倒數
1
κ
(
t
)
{\displaystyle {\frac {1}{\kappa (t)}}}
稱為曲率半徑 。
半徑為 r 的圓周有常曲率
κ
(
t
)
=
1
r
,
{\displaystyle \kappa (t)={\frac {1}{r}}\,,}
但一條直線的曲率是 0 。
次法向量 是第三個 Frenet 向量 e 3 (t ) ,
總是正交於 t 點的單位 切向量和單位法向量。其定義為
e
3
(
t
)
=
e
3
¯
(
t
)
‖
e
3
¯
(
t
)
‖
e
3
¯
(
t
)
=
γ
‴
(
t
)
−
⟨
γ
‴
(
t
)
,
e
1
(
t
)
⟩
e
1
(
t
)
−
⟨
γ
‴
(
t
)
,
e
2
(
t
)
⟩
e
2
(
t
)
{\displaystyle \mathbf {e} _{3}(t)={\frac {{\overline {\mathbf {e} _{3}}}(t)}{\|{\overline {\mathbf {e} _{3}}}(t)\|}}\quad {\overline {\mathbf {e} _{3}}}(t)=\mathbf {\gamma } '''(t)-\langle \mathbf {\gamma } '''(t),\mathbf {e} _{1}(t)\rangle \,\mathbf {e} _{1}(t)-\langle \mathbf {\gamma } '''(t),\mathbf {e} _{2}(t)\rangle \,\mathbf {e} _{2}(t)}
在 3 維空間中等式簡化為
e
3
(
t
)
=
e
2
(
t
)
×
e
1
(
t
)
.
{\displaystyle \mathbf {e} _{3}(t)=\mathbf {e} _{2}(t)\times \mathbf {e} _{1}(t)\,.}
第二廣義曲率 χ2 (t ) 稱為撓率 ,度量了 γ 和一條平面曲線的偏離程度。或者說,如果撓率為 0 則曲線完全在某平面內(任何 t 都在這一個平面內)。
τ
(
t
)
=
χ
2
(
t
)
=
⟨
e
2
′
(
t
)
,
e
3
(
t
)
⟩
‖
γ
′
(
t
)
‖
{\displaystyle \tau (t)=\chi _{2}(t)={\frac {\langle \mathbf {e} _{2}'(t),\mathbf {e} _{3}(t)\rangle }{\|\mathbf {\gamma } '(t)\|}}}
稱為 γ 在點 t 的撓率 。
給定 n 個函數
χ
i
∈
C
n
−
i
(
[
a
,
b
]
)
,
1
≤
i
≤
n
{\displaystyle \chi _{i}\in C^{n-i}([a,b]){\mbox{, }}1\leq i\leq n}
滿足
χ
i
(
t
)
>
0
,
1
≤
i
≤
n
−
1
{\displaystyle \chi _{i}(t)>0{\mbox{, }}1\leq i\leq n-1}
那麼存在惟一的 (在差一個歐幾里得群 作用的意義下) n 階正則 C n +1
‖
γ
′
(
t
)
‖
=
1
(
t
∈
[
a
,
b
]
)
{\displaystyle \|\gamma '(t)\|=1{\mbox{ }}(t\in [a,b])}
χ
i
(
t
)
=
⟨
e
i
′
(
t
)
,
e
i
+
1
(
t
)
⟩
‖
γ
′
(
t
)
‖
,
{\displaystyle \chi _{i}(t)={\frac {\langle \mathbf {e} _{i}'(t),\mathbf {e} _{i+1}(t)\rangle }{\|\mathbf {\gamma } '(t)\|}}\,,}
這裡集合
e
1
(
t
)
,
…
,
e
n
(
t
)
{\displaystyle \mathbf {e} _{1}(t),\ldots ,\mathbf {e} _{n}(t)}
是曲面的 Frenet 標架。
再附加起始 t 0 ∈ I ,起始點 p 0 ∈ R n e 1 , ..., e n -1
γ
(
t
0
)
=
p
0
{\displaystyle \mathbf {\gamma } (t_{0})=\mathbf {p} _{0}}
e
i
(
t
0
)
=
e
i
,
1
≤
i
≤
n
−
1
{\displaystyle \mathbf {e} _{i}(t_{0})=\mathbf {e} _{i}{\mbox{, }}1\leq i\leq n-1}
那麼我們可以排除歐幾里得作用得到惟一的曲線 γ。
Frenet-Serret 公式是一組一階常微分方程 。其解為由廣義曲率函數 χi
[
e
1
′
(
t
)
e
2
′
(
t
)
]
=
[
0
κ
(
t
)
−
κ
(
t
)
0
]
[
e
1
(
t
)
e
2
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\mathbf {e} _{2}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\kappa (t)\\-\kappa (t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\mathbf {e} _{2}(t)\\\end{bmatrix}}}
[
e
1
′
(
t
)
e
2
′
(
t
)
e
3
′
(
t
)
]
=
[
0
κ
(
t
)
0
−
κ
(
t
)
0
τ
(
t
)
0
−
τ
(
t
)
0
]
[
e
1
(
t
)
e
2
(
t
)
e
3
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\mathbf {e} _{2}'(t)\\\mathbf {e} _{3}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\kappa (t)&0\\-\kappa (t)&0&\tau (t)\\0&-\tau (t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\mathbf {e} _{2}(t)\\\mathbf {e} _{3}(t)\\\end{bmatrix}}}
[
e
1
′
(
t
)
⋮
e
n
′
(
t
)
]
=
[
0
χ
1
(
t
)
0
−
χ
1
(
t
)
⋱
⋱
⋱
0
χ
n
−
1
(
t
)
0
−
χ
n
−
1
(
t
)
0
]
[
e
1
(
t
)
⋮
e
n
(
t
)
]
{\displaystyle {\begin{bmatrix}\mathbf {e} _{1}'(t)\\\vdots \\\mathbf {e} _{n}'(t)\\\end{bmatrix}}={\begin{bmatrix}0&\chi _{1}(t)&&0\\-\chi _{1}(t)&\ddots &\ddots &\\&\ddots &0&\chi _{n-1}(t)\\0&&-\chi _{n-1}(t)&0\\\end{bmatrix}}{\begin{bmatrix}\mathbf {e} _{1}(t)\\\vdots \\\mathbf {e} _{n}(t)\\\end{bmatrix}}}
Erwin Kreyszig, Differential Geometry , Dover Publications, New York, 1991, ISBN 9780484667218 . Chapter II is is a classical treatment of Theory of Curves in 3-dimensions.
陳維桓,微分幾何,北京大學出版社,北京,2006年,ISBN 7-301-10709.
















![{\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58e103c376cd9ea50b5c12c8f5398ded4d2a3577)

































![{\displaystyle \chi _{i}\in C^{n-i}([a,b]){\mbox{, }}1\leq i\leq n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccea8628d1a310cfb40f69917da1a4124b60fcc7)

![{\displaystyle \|\gamma '(t)\|=1{\mbox{ }}(t\in [a,b])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1f0d59be10764f3c9481cb70324bfdb72331222)





