主題:幾何學/特色條目
用法
The layout design for these subpages is at Portal:幾何學/特色條目/Layout.
- Add a new Selected article to the next available subpage.
- Update "max=" to new total for its {{Random portal component}} on the main page.
特色條目列表
特色條目 1
勾股定理是人類早期發現並證明的重要數學定理之一。
據《周髀算經》中記述,公元前一千多年周公與商高論數的對話中,商高就以三四五3個特定數為例詳細解釋了勾股定理要素,其一,「以為句廣三,股修四,徑隅五」。其二,「既方其外,半之一矩,環而共盤,得成三四五。兩矩共長二十有五,是謂積矩。」首先肯定一個底寬為三,高為四的直角三角形,弦長必定是五。最重要的是緊接着論證了弦長平方必定是兩直角邊的平方和,確立了直角三角形兩條直角邊的平方和等於斜邊平方的判定原則。其判定方法後世不明其法而被忽略。
此外,《周髀算經》中明確記載了周公後人陳子敘述的勾股定理公式:「若求邪至日者,以日下為勾,日高為股,勾股各自乘,並而開方除之,得邪至日」。
趙爽在《周髀算經注》中將勾股定理表述為「勾股各自乘,並之,為弦實。開方除之,即弦」。
古埃及在公元前2600年的紙莎草就有(3,4,5)這一組勾股數,而古巴比倫泥板涉及的最大的一個勾股數組是(18541,12709,13500)。
古希臘發現勾股定理的是畢達哥拉斯,所以勾股定理又稱畢達哥拉斯定理。據說畢達哥拉斯證明了這個定理後,即斬了百頭牛作慶祝(百牛大祭),因此又稱百牛定理。但這個說法顯然是以訛傳訛,眾所周知畢達哥拉斯主義者在古代以素食聞名。
特色條目 2
正圖形是正多邊形(例如,正方形或者正五邊形)和正多面體(例如立方體)的向任意維度的推廣類比。正圖形極強的對稱性使它們擁有極強的審美價值,吸引着數學家和數學愛好者。
一般地,n維正圖形被定義為有正維面[(n − 1)-表面]和正頂點圖。這兩個條件已經能充分地保證所有面、所有頂點都是相似的。但要注意的是,這一定義並不適用於抽象多胞形。
一個正圖形能用形式為{a, b, c, ...., y, z}的施萊夫利符號代表,其正的面為{a, b, c, ..., y},頂點圖為{b, c, ..., y, z}。
特色條目 3
常見的三角函數包括正弦函數()、餘弦函數()和正切函數(或者)。在航海學、測繪學、工程學等其他學科中,還會用到如餘切函數、正割函數、餘割函數、正矢函數、半正矢函數等其他的三角函數。不同的三角函數之間的關係可以通過幾何直觀或者計算得出,稱為三角恆等式。
三角函數一般用於計算三角形中未知長度的邊和未知的角度,在導航、工程學以及物理學方面都有廣泛的用途。另外,以三角函數為模版,可以定義一類相似的函數,叫做雙曲函數。常見的雙曲函數也被稱為雙曲正弦函數、雙曲餘弦函數等等。
特色條目 4
它被認為是最成功的教科書之一:《幾何原本》是第一本要出版的書之一,並且僅次於《聖經》,出版的版本數量超過1000種。幾個世紀以來,當所有大學生的課程都被納入時,所有學生都要求至少部分歐幾里德幾何原本的知識。直到20世紀才被認為是所有受過教育的人都讀過的東西。 它仍然(雖然很少)用作今天的幾何學基本介紹。
這本著作是在四庫全書中為子部天文演算法算書類。
特色條目 5
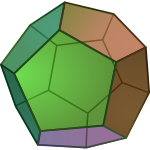
由於它們的審美美感和對稱性,柏拉圖立體已成為幾千年來幾何學家們的一個最喜歡的主題。他們以古希臘哲學家柏拉圖命名,聲稱古典元素是從正多面體構建的。
正多面體的別稱柏拉圖立體是因柏拉圖而命名的。柏拉圖的朋友泰阿泰德告訴柏拉圖這些立體,柏拉圖便將這些立體寫在《蒂邁歐篇》(Timaeus) 內。正多面體的作法收錄《幾何原本》的第13卷。在命題13描述正四面體的作法;命題14為正八面體作法;命題15為立方體作法;命題16則是正二十面體作法;命題17則是正十二面體作法。
特色條目 6
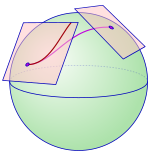
任何維數為正數的流形都會有無窮個仿射聯絡。仿射聯絡能用來決定在向量場上求導,並滿足線性及萊布尼茲法則的方法,這表明了仿射聯絡有幾個可行的方法,像是協變導數或在向量叢上的聯絡。仿射聯絡也能用來決定在切向量沿著一條曲線平行移動的方式,或者用來決定標架叢的平行移動。仿射聯絡也可以用來決定流形上的測地線,推廣了歐幾里德空間中直線的概念。
候選
- Adding articles
- Feel free to add any featured or good articles to the list above. You can also nominate other articles relating to PlayStation here.
- If you are unsure or do not know how to add an entry, please ask for help at the Portal talk:Sony PlayStation talk page.