使用者:AnthonyDonlon/wip/維特比解碼器
維特比解碼器使是一種使用維特比算法的解碼器,可以對卷積碼或網格碼編碼的比特流進行解碼。
除了維特比算法外,還有其他算法可對卷積碼進行解碼(如Fano 算法)。 相比之下,維特比算法最消耗資源,但它可以進行最大似然解碼。它最常用於解碼約束長度 k ≤ 3 的卷積碼,但實際使用的值高達 k=15。
維特比解碼由 Andrew J. Viterbi 開發並發表在論文 Viterbi, A. Error Bounds for Convolutional Codes and an Asymptotically Optimum Decoding Algorithm. IEEE Transactions on Information Theory. April 1967, 13 (2): 260–269. doi:10.1109/tit.1967.1054010. 「卷積碼的誤差界限和漸近最優解碼算法」。 IEEE 信息論彙刊。 13 (2): 260–269。 doi : 10.1109/tit.1967.1054010 。
Viterbi 解碼器有硬件(如應用在調製解調器中)和軟件實現。
維特比解碼用於迭代維特比解碼算法。
硬件實現
[編輯]
用於基本(未穿孔)代碼的硬件維特比解碼器通常由以下主要模塊組成:
- 分支度量單元 (Branch metric unit, BMU)
- 路徑度量單位(Path metric unit, PMU)
- 回溯單元 (Traceback unit, TBU)
分支度量單元 (BMU)
[編輯]
分支度量單元的功能是計算分支度量,它是代碼字母表中每個可能符號與接收符號之間的歸一化距離。
維特比解碼器的判決方式被分為硬判決和軟判決。硬判決維特比解碼器將簡單的比特流作為輸入,並用漢明距離作為每個符號的度量。而軟判決維特比解碼器接收的比特流還包含關於每個接收符號的可靠性的信息。例如,如果使用 3 位編碼,可靠性信息可以編碼如下:
| 值 | 含義 | |
|---|---|---|
| 000 | 最強 | 0 |
| 001 | 比較強 | 0 |
| 010 | 比較弱 | 0 |
| 011 | 最弱的 | 0 |
| 100 | 最弱的 | 1 |
| 101 | 比較弱 | 1 |
| 110 | 比較強 | 1 |
| 111 | 最強 | 1 |
當然,這不是唯一對可靠性數據進行編碼的方法。
在軟判決解碼器中,歐幾里得距離的平方值常用作度量值。
路徑度量單元(PMU)
[編輯]
路徑度量單元總結了分支度量以獲取度量路徑,其中 K 是代碼的約束長度,最終可以選擇其中之一作為優化。它製造的每一個時鐘決策,故意拋棄非最佳路徑。這些決定的結果被寫入回溯單元的內存中。
PMU 的核心元素是ACS(相加-比較-選擇)單元。它們之間的連接方式由特定代碼的網格圖定義。
由於分支指標總是 ,必須有一個額外的電路(圖中未顯示)防止公制計數器溢出。無需監視路徑度量增長的另一種方法是允許路徑度量「滾動」;要使用此方法,必須確保路徑度量累加器包含足夠的位以防止「最佳」和「最差」值彼此相差 2 (n-1) 以內。比較電路基本上沒有變化。

通過監控「最佳」路徑度量的增長率,可以監控傳入比特流上的噪聲水平。一種更簡單的方法是監視單個位置或「狀態」並觀察它「向上」通過累加器範圍內的四個離散級別。當它向上通過這些閾值中的每一個時,計數器會遞增,以反映傳入信號中存在的「噪聲」。
回溯單元 (TBU)
[編輯]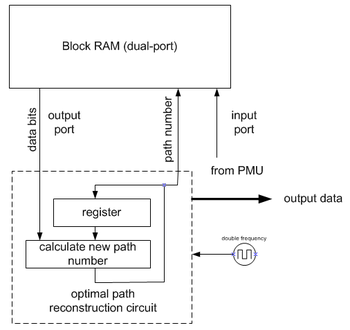
回溯單元從路徑度量單元的輸出中恢復(幾乎)最大似然路徑。由於它是在相反的方向上進行的,因此維特比解碼器包括一個 FILO(先進後出)緩衝器來重建正確的順序。
請注意,圖像上顯示的實現需要雙倍頻率。有一些技巧可以消除這種要求。
實現問題
[編輯]軟判決解碼的量化
[編輯]為了充分利用軟判決解碼的優勢,需要對輸入信號進行適當的量化。最佳量化區寬度由以下公式定義:
在哪裡是噪聲功率譜密度, k是軟判決的位數。
歐幾里得度量的計算
[編輯]平方範數( ) 碼字母表中接收到的符號和實際符號之間的距離可以進一步簡化為線性和/差形式,從而降低計算強度。
考慮一個1/2卷積編碼器,其產生對每個輸入位(1或0)的2位'(00,01,10'或11)。這些歸零信號被轉換為旁邊顯示的非歸零形式。
| 代碼字母表 | 矢量映射 |
|---|---|
| 00 | +1, +1 |
| 01 | +1,-1 |
| 10 | −1, +1 |
| 11 | -1, -1 |
每個接收符號可以向量形式表示為v r = {r 0, r 1 },其中r 0和r 1是軟判決值,其大小表示接收向量v r的聯合可靠性。
歐幾里得距離度量的實際計算是:
每個平方項是一個賦范距離,描述了符號的能量。例如,符號v i = {±1, ±1}的能量可以計算為
因此,代碼字母表中所有符號的能量項是常數(在(歸一化)值 2 處)。
Add-Compare-Select ( ACS ) 操作比較接收到的符號||v r || 之間的度量距離以及代碼字母表中的任何 2 個符號,其路徑在相應格子中的節點處合併, ||v i (0) ||和||v i (1) || .這相當於比較
和
但是,從上面我們知道v i的能量是常數(等於(歸一化)值 2),並且v r的能量在兩種情況下是相同的。這減少了與 2 個(中間)點積項之間的最小值函數的比較,
因為min操作可能被解釋為對正數max
每個點積項可以擴展為
其中,每一項的符號取決於要比較的符號v i (0)和v i (1) 。因此,可以用簡單的加/減操作來執行平方歐幾里德度量距離計算以計算分支度量。
回溯
[編輯]回溯的一般方法是累積最多五倍約束長度(5( K -1))的路徑度量,找到累積成本最大的節點,並從該節點開始回溯。
卷積碼的存儲器(約束長度 K -1)的五倍截斷深度的常用經驗法則僅對速率 1/2 碼是準確的。對於任意速率,準確的經驗法則是 2.5( K - 1)/(1− r ),其中r是碼率。 [1]
然而,計算累積最大成本(最大或最小的積分路徑度量)的節點涉及找到幾個(通常為 2 K -1 )數的最大值或最小值,這在嵌入式硬件系統上實現時可能很耗時。
大多數通信系統採用維特比解碼,涉及固定大小的數據包,在數據包的開頭或/和結尾具有固定的位/字節模式。通過使用已知的位/字節模式作為參考,可以將起始節點設置為固定值,從而在回溯期間獲得完美的最大似然路徑。
限制
[編輯]由於輸入信號的量化、分支和路徑度量以及有限的回溯長度,維特比解碼器的物理實現不會產生精確的最大似然流。實際實現確實接近理想值的 1dB 以內。
維特比解碼器的輸出,在解碼被加性高斯信道損壞的消息時,錯誤分組為錯誤突發。 [2] [3]單單糾錯碼無法糾正此類突發,因此卷積碼和維特比解碼器必須設計得足夠強大以將錯誤降低到可接受的速率,或者必須使用突發糾錯碼。
打孔代碼
[編輯]打孔碼的硬件維特比解碼器通常以這樣的方式實現:
- 一個 depuncturer,它將輸入流轉換為看起來像原始(未打孔)流的流,在位被擦除的位置帶有 ERASE 標記。
- 理解這些 ERASE 標記的基本維特比解碼器(即,不將它們用於分支度量計算)。
軟件實現
[編輯]在軟件實現中,最耗時的操作之一是 ACS 的蝶形運算過程,通常使用匯編語言和適當的指令集擴展(例如SSE2 )來實現,以加快解碼時間。
應用
[編輯]維特比解碼算法廣泛應用於以下領域:
- 無線電通信:數字電視( ATSC 、 QAM 、 DVB-T等)、無線電中繼、衛星通信、業餘無線電的PSK31數字模式。
- 解碼網格編碼調製(TCM,電話線調製解調器中使用的一種技術),可從 3 kHz的帶寬 個中擠出高頻譜效率 kHz 帶寬模擬電話線。
- 計算機存儲設備,如硬盤驅動器。
- 自動語音識別
參考
[編輯]
外部連結
[編輯]- Forney. The Viterbi Algorithm: A Personal History. arXiv:cs/0504020
 .
. - Details on Viterbi decoding, as well as a bibliography.
- Viterbi algorithm explanation with the focus on hardware implementation issues.
- r=1/6 k=15 coding for the Cassini mission to Saturn.
- Online Generator of optimized software Viterbi decoders (GPL).
- GPL Viterbi decoder software for four standard codes.
- Description of a k=24 Viterbi decoder, believed to be the largest ever in practical use.
- Generic Viterbi decoder hardware (GPL).
[[Category:错误检测与校正]] [[Category:資料傳輸]]
- ^ B. Moision, "A truncation depth rule of thumb for convolutional codes," 2008 Information Theory and Applications Workshop, San Diego, CA, 2008, pp. 555-557, doi:10.1109/ITA.2008.4601052.
- ^ Stefan Host, Rolf Johannesson, Dmitrij K. Zigangirod, Kamil Sh. Zigangirod, and Viktor V. Zyablod. "On the Distribution of the Output Error Burst Lengths for Viterbi Decoding of Convolutional Codes".
- ^ Curry, S. J.; Harmon, W. D. "A bound on Viterbi decoder error burst length".











