余樹江
| 余樹江[1] Kane S. Yee | |
|---|---|
| 出生 | 1934年3月26日 |
| 公民權 | |
| 母校 | 柏克萊加州大學 |
| 知名於 | 時域有限差分法 |
| 科學生涯 | |
| 研究領域 | |
| 機構 | |
| 論文 |
|
| 博士導師 | 伯納德·佛利民 (Bernard Friedman) |
余樹江[1](英語:Kane Shee-Gong Yee,1934年3月26日—),美籍華裔電氣工程師、應用數學家、電磁學家。他的研究領域涉及電磁學、流體力學、連續介質力學[2],以及偏微分方程式的數值分析。[3]余樹江最知名的工作是1966年提出求解麥克斯韋方程組的一種算法:時域有限差分法(FDTD)。[4]時域有限差分法使物理學家與工程師能直接用計算機模擬電磁波在空間中的傳播與演化[4],在計算電磁學、光學、微波無線電、電子設計自動化中有着重要應用。時域有限差分法的基本運算單元「余氏網格」(英語:Yee's cell)就是以他的姓氏命名的。
生平
[編輯]余樹江於1934年3月26日在中國廣東省廣州市出生。1957年,獲得美國柏克萊加州大學電氣工程學士學位[5],1958年獲得碩士學位,論文題目為《有限壁厚的圓柱空腔諧振器的分析》。[3]隨後,在同校的伯納德·佛利民(Bernard Friedman)教授的指導下進修數學,1963年獲得應用數學博士學位,博士論文的課題是《麥克斯韋方程組的邊值問題》。[6]1959年至1961年,受聘於洛歇導彈與航天公司(Lockheed Missiles and Space Company),研究電磁波繞射的問題。[3]
在自學Fortran編程時,作為練習,余樹江開始嘗試用計算機模擬麥克斯韋方程組。[4]1966年,余樹江在《IEEE天線與傳播期刊》上發表論文,提出一種在交錯式網格上應用有限差分法以求解麥克斯韋方程組的算法。[7]這使物理學家與工程師能直接用計算機模擬電磁波在空間中的傳播與演化,是計算電磁學發展的里程碑。然而由於多種原因,當時這篇論文在學術界幾乎無人關注,直到90年代隨計算機的發展才開始廣泛應用。[4]1980年,本算法被命名為時域有限差分法。[8]為了紀念余樹江的貢獻,本算法有時也稱為「余氏算法」(Yee's method),其基本運算單元「余氏網格」(Yee's cell)也是以他的姓氏命名的。[9][10]
1966至1984年間,余樹江在佛羅里達大學電氣工程系與數學系擔任教授,隨後又在堪薩斯州立大學擔任教授。1966年,擔任勞倫斯利弗莫爾國家實驗室顧問,並在1984至1987年間從事微波脆弱性(microwave vulnerability)的研究。1987年,擔任洛歇公司帕洛阿爾托研究實驗室的研究員,研究計算電磁學問題。1996年退休。[2]
時域有限差分法
[編輯]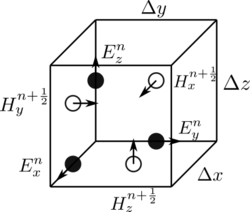
1966年,余樹江在《IEEE天線與傳播期刊》上發表論文,提出一種在交錯式網格上應用有限差分法以求解麥克斯韋方程組的算法。[7]這使物理學家與工程師能直接用計算機模擬電磁波在空間中的傳播與演化,是計算電磁學發展的里程碑。然而由於多種原因,當時這篇論文在學術界幾乎無人關注——電磁學界當時普遍使用頻域法而非時域法;創建入射電磁波的初始條件算法缺乏效率;吸收邊界條件在當時尚未提出,無法計算開放邊界的輻射問題(如天線);缺乏實驗驗證;計算機也不甚發達。直到90年代隨計算機的發展,時域有限差分法才開始廣泛應用。[4]
1969年,學者Dong-Hoa Lam改正了原論文中不正確的數值穩定性條件。[11]1975年,艾倫·泰福勒(Allen Taflove)與莫里斯·E·布羅德溫(Morris E. Brodwin)也改正了本錯誤,並進一步推廣了余樹江的成果。[12]1980年,本算法被命名為時域有限差分法。[8]為了紀念余樹江的貢獻,本算法有時也稱為「余氏算法」(Yee's method),其基本運算單元「余氏網格」(Yee's cell)也是以他的姓氏命名的。[9][10]
部分著作
[編輯]- Yee, Kane S. Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media [麥克斯韋方程組在各向同性介質中的初值與邊值問題的數值解] (PDF). IEEE Transactions on Antennas and Propagation. May 1966, 14 (3): 302–307 [2023-02-27]. doi:10.1109/TAP.1966.1138693. (原始內容存檔 (PDF)於2019-07-12).
- Taflove, A.; Umashankar, K.R.; Beker, B.; Harfoush, F.; Yee, K.S. Detailed FD-TD analysis of electromagnetic fields penetrating narrow slots and lapped joints in thick conducting screens [應用時域有限差分法對電磁場穿透厚導電屏蔽層上狹窄縫隙與搭接接頭的詳盡分析]. IEEE Transactions on Antennas and Propagation. February 1988, 36 (2): 247–257. doi:10.1109/8.1102.
- Yee, K.S.; Ingham, D.; Shlager, K. Time-domain extrapolation to the far field based on FDTD calculations [基於時域有限差分法的時域遠場外推]. IEEE Transactions on Antennas and Propagation. March 1991, 39 (3): 410–413. doi:10.1109/8.76342.
- Zivanovic, S.S.; Yee, K.S.; Mei, K.K. A subgridding method for the time-domain finite-difference method to solve Maxwell's equations [時域有限差分法求解麥克斯韋方程組的一種子網格法]. IEEE Transactions on Microwave Theory and Techniques. March 1991, 39 (3): 471–479. doi:10.1109/22.75289.
- Yee, K.S.; Chen, J.S.; Chang, A.H. Conformal finite difference time domain (FDTD) with overlapping grids [具有重疊網格的共形時域有限差分]. IEEE Antennas and Propagation Society International Symposium 1992 Digest. June 1992. doi:10.1109/APS.1992.221489.
- Yee, Kane S.; Chen, Jei S. The finite-difference time-domain (FDTD) and the finite-volume time-domain (FVTD) methods in solving Maxwell's equations [時域有限差分法(FDTD)與時域有限體積法(FVTD)對麥克斯韋方程組的求解]. IEEE Transactions on Antennas and Propagation. March 1997, 45 (3): 354–363. doi:10.1109/8.558651.
參見
[編輯]參考資料
[編輯]- ^ 1.0 1.1 Pu Zhang. What's Kane S. Yee who invented FDTD in Chinese?. Stack Exchange. 2022-09-20 [2023-05-05]. (原始內容存檔於2023-03-10).
I've got the answer to my own question through private communication. The Chinese name of the inventor of computational electrodynamics technique, or finite-difference time domain method, is 余樹江.
- ^ 2.0 2.1 Yee, Kane S.; Chen, Jei S. The finite-difference time-domain (FDTD) and the finite-volume time-domain (FVTD) methods in solving Maxwell's equations. IEEE Transactions on Antennas and Propagation. March 1997, 45 (3): 354–363. doi:10.1109/8.558651.
- ^ 3.0 3.1 3.2 Yee, Kane S. A Closed-Form Expression for the Energy Dissipation in a Low-Loss Transmission Line. IEEE Transactions on Nuclear Science. February 1974, 21 (1): 1006–1008. doi:10.1109/TNS.1974.4327594.
- ^ 4.0 4.1 4.2 4.3 4.4 Pile, David. Numerical solution: Interview with Allen Taflove. Nature Photonics. 23 December 2014, 9: 5–6. doi:10.1038/nphoton.2014.305.
- ^ Yee, Kane Shee-Gong. Analysis of a cylindrical cavity resonator with finite wall thickness (學位論文). University of California, Berkeley. 1958.
- ^ Yee, Kane. Boundary-value problems for Maxwell's equations (PDF) (學位論文). University of California, Berkeley. March 1963 [2023-03-10]. (原始內容存檔 (PDF)於2023-03-10).
- ^ 7.0 7.1 Yee, Kane S. Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media (PDF). IEEE Transactions on Antennas and Propagation. May 1966, 14 (3): 302–307 [2023-02-27]. doi:10.1109/TAP.1966.1138693. (原始內容存檔 (PDF)於2019-07-12).
- ^ 8.0 8.1 Taflove, A. Application of the finite-difference time-domain method to sinusoidal steady state electromagnetic penetration problems (PDF). IEEE Transactions on Electromagnetic Compatibility. 1980, 22 (3): 191–202 [2023-02-27]. Bibcode:1980ITElC..22..191T. doi:10.1109/TEMC.1980.303879. (原始內容存檔 (PDF)於2021-01-18).
- ^ 9.0 9.1 Taflove, Allen; Hagness, Susan. Computational Electrodynamics: The Finite-Difference Time-Domain Method 2. Norwood, MA: Artech House. 2000: 75-79. ISBN 1580530761.
- ^ 10.0 10.1 Inan, Umran; Marshall, Robert A. Numerical Electromagnetics: The FDTD Method 2. New York, NY: Cambridge University Press. 2011: 72-74. ISBN 1139497987.
- ^ Lam, Dong-Hoa. Finite Difference Methods for Electromagnetic Scattering Problems. Mississippi State University, Interaction Notes. 1969, 44.
- ^ Taflove, A.; Brodwin, M. E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell's equations (PDF). IEEE Transactions on Microwave Theory and Techniques. 1975, 23 (8): 623–630 [2023-02-27]. Bibcode:1975ITMTT..23..623T. doi:10.1109/TMTT.1975.1128640. (原始內容存檔 (PDF)於2021-01-26).
