在三稜鏡 中,材料色散效應(折射率 與波長 有關的現象)使不同顏色的光以不同角度折射 ,將白光分成光譜 。 透過阿米西稜鏡 觀察慳電膽 的色散。 在光學 中,色散 ( saan3 ) [ 1] Dispersion )是光波 的相速度 隨着頻率而改變的現象。[ 2] 色散 ( saan3 ) (英語:dispersive medium )。
儘管色散這一術語在光學領域用於描述光波 和其他電磁波 ,但相同意義上的「散失」適用於任何類型的波,例如可產生頻散 的聲波和地震波,以及海浪中的重力波 。光學中的散失還可以描述輸電線 信號(如同軸電纜 中的微波 )或光纖 中脈衝的特性;而物理能量上的散失是指動能被吸收的現象。
在光學中,色散的主要現象是不同顏色的光在透過三稜鏡 或有色差 的透鏡時因折射角 不同,而產生光譜。[ 3] 消色差透鏡 的設計在極大消除了色差,並通過阿貝數
V
{\displaystyle V}
可見光譜 色散。在電信應用中,波包 或「脈衝」的傳輸往往比波的絕對相位更重要,此時就需要考慮並計算波包的群速度色散
所有常見的傳輸介質 的衰減 (歸一化為傳輸長度)也隨頻率而變化,從而導致衰減失真 阻抗邊界 (例如電纜中的壓接段)處的反射會產生信號失真,並進一步加劇在信號帶寬上觀察到的不一致的傳輸時間。
彩虹 可能是最常見的色散現象。色散導致太陽光 在空間上分離成不同波長 (不同顏色 )的部分。然而,色散在許多其他情況下也會產生影響:例如,群速度色散 導致脈衝 在光纖 中擴散,使長距離的信號衰減;此外,群速度色散和非線性 效應之間的抵消會導致孤波 產生。
大部分情況下,色散研究的是散装材料的色散。然而,在波導管 中也存在着波導色散 (英語:waveguide dispersion ),在這種情況下,波在結構中的相速度 取決於其頻率,這僅僅是由於結構的幾何形狀。更廣泛地說,波導色散可以發生在通過任何不均勻結構(如光子晶體 )傳播的波中,無論這些波是否被限制在某些區域。[可疑 在波導管中,兩種 類型的色散通常都會存在,儘管它們不是嚴格意義上的相加。[來源請求] 零色散波長 ,這有助於光纖通信 速度的提高。
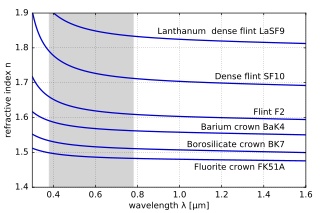
不同玻璃,真空折射率與波長的關係。可見光範圍以灰色區域表示。 在光學上,材料色散有優點也有缺點。透過三棱鏡,光的色散為製作光譜儀 以及分光輻射計 的基礎。有時候也會透過全像 光柵,來達成更顯著的分光效果。然而,在透鏡中的色散效應造成影像品質低落,在顯微鏡、望遠鏡及其他成像技術上可見一斑。
在均勻介質中,波傳遞的相速度 為
v
=
c
n
{\displaystyle v={\frac {c}{n}}}
其中,c 為真空中的光速,而 n 為介質的折射率。
對於不同波長 的光,介質 的折射率 n (λ ) 也不同。這個關係式通常由阿貝數 可以計算出,或是由柯西等式 或Sellmeier等式 的系數求得。
由克拉莫-克若尼關係式 ,波長與實部折射率的關係與材料的吸收率有關,此吸收率由折射率的虛部(或稱消光系數 )。在非磁性物質中,克拉莫-克若尼關係式的χ 為電極化率χ e = n 2 − 1.
對於可見光 ,一般的透明材料:
如果
λ
r
>
λ
y
>
λ
b
{\displaystyle \lambda _{\rm {r}}>\lambda _{\rm {y}}>\lambda _{\rm {b}}}
那麼
1
<
n
(
λ
r
)
<
n
(
λ
y
)
<
n
(
λ
b
)
{\displaystyle 1<n(\lambda _{\rm {r}})<n(\lambda _{\rm {y}})<n(\lambda _{\rm {b}})}
或可用以下表達式表示:
d
n
d
λ
<
0
{\displaystyle {\frac {{\mathrm {d} }n}{{\mathrm {d} }\lambda }}<0}
在此狀況下,此介質擁有正常頻散 。然而,當折射率隨着波長增加而增加時(通常在紫外光區發現[ 4] 反常頻散 。
法國 數學家 柯西 發現折射率和光波長的關係,可以用一個級數 表示:
n
(
λ
)
=
B
+
C
λ
2
+
D
λ
4
+
⋯
{\displaystyle n(\lambda )=B+{\frac {C}{\lambda ^{2}}}+{\frac {D}{\lambda ^{4}}}+\cdots }
其中,B、C、D 是三個柯西色散係數,由物質的種類決定。只需測定三個不同波長的光的折射率 n (λ ),代入柯西色散公式中,便可得到三個聯立方程式。解這組聯立方程式就可以得到這種物質的三個柯西色散係數。有了三個柯西色散係數,就可以計算出其他波長的光的折射率,而不需要再進行測量。
除了柯西色散公式之外,還有其他的色散公式,如:Hartmann色散公式、Conrady色散公式、Hetzberger色散公式等。
在一種假想介質(k=ω²)中傳播的短時脈衝的時間演化。這體現了長波成分比短波成分傳播要更快(正群速度色散),產生啁啾和脈衝變寬。 色散的效應遠不止是使得相速度隨着波長變化,更重要的是它產生一種叫做群速度色散 的效應。相速度 v 被定義為 v = c / n 群速度 。群速度描述了一個脈衝或者信號中的信息隨着波動傳播的速度。在旁邊的動圖中,我們可以發現波動本身(橙色)以相速度移動,這個速度要比波包(黑色)代表的群速度更快。舉個例子,這個脈衝可能是一個通訊信號,其內的信息只能以群速度傳播,儘管它由速度更快的波前組成。
從折射率曲線 n (ω ),我們可以算出群速度。或者用一種更直接的計算方式。首先我們計算波數 k = ωn/c ,其中,ω =2πf 是角頻率。這樣,相速度的公式是vp =ω/k ,而群速度的計算公式可以用導數 v g =dω/dk 表示。或者,群速度也可以用相速度 vp 表示:
v
g
=
v
p
1
−
ω
v
p
d
v
p
d
ω
.
{\displaystyle {\rm {v_{g}}}={\frac {\rm {v_{p}}}{1-{\frac {\omega }{\rm {v_{p}}}}{\frac {\rm {dv_{p}}}{d\omega }}}}.}
當存在色散的時候,群速度不但不等於相速度,它還會隨着波長變化。這種現象被稱作群速度色散(Group Velocity Dispersion, GVD),也導致一個脈衝會變寬,這是因為脈衝里含有多個頻率的成分,它們的速度不同。群速度色散可以用群速度的倒數 對角頻率的導數 d2 k/dω2 來定量描述。
如果一個光脈衝在介質中的傳播具有正群速度色散,那麼短波成分的群速度就小於長波成分的群速度,這個脈衝就是正啁啾 的 (up-chirped),它的頻率隨着時間升高。 反之,如果一個光脈衝在介質中的傳播具有負群速度色散,那麼短波成分的群速度就大於長波成分的群速度,這個脈衝就是負啁啾 的 (down-chirped),它的頻率隨着時間降低。
群速度色散參數 :
D
=
−
λ
c
d
2
n
d
λ
2
.
{\displaystyle D=-{\frac {\lambda }{c}}\,{\frac {{\rm {d}}^{2}n}{{\rm {d}}\lambda ^{2}}}.}
經常被用來定量描述群速度色散。D 和群速度色散的比值是一個負的係數:
D
=
−
2
π
c
λ
2
d
2
k
d
ω
2
.
{\displaystyle D=-{\frac {2\pi c}{\lambda ^{2}}}\,{\frac {{\rm {d}}^{2}k}{{\rm {d}}\omega ^{2}}}.}
一些書的作者把折射率對波長的二階導數 大於0(或小於0),也即D 小於0(或大於0),稱為正常色散/反常色散。[ 5]
不論是負還是正的群速度色散,其最終結果皆為脈衝在時間上的擴展。這使得色散在管理在基於光纖的光學通訊系統中十分重要。因為如果色散過於強烈,對應於一組比特的一系列脈衝將在時域擴散開並相互混合,使得信號無法被解讀。這限制了信號在光纖中傳輸的距離(如果沒有進行信號重新生成)。
此問題的可能解法之一是在光纖中傳輸群速度色散為0的信號(例如,在矽纖維中 1.3–1.5 μm 的信號),此波長的信號在傳輸過程中的色散可以控制到最小。
然而,在實務上,這種做法引發的問題比其解決的問題要麻煩很多:群色散為0的信號放大了其他非線性效應(例如四波混頻 )。
另一種選項是在負色散區域使用孤子 脈衝,其特性是它利用非線性光學效應保持自身形狀。然而,孤子的現實問題是它需要脈衝具有一定水平的功率以保證非線性光學的效應的強度正確。
目前,實際使用的方案是進行色散補償,一般是將具有相反符號色散效應的光纖組合起來把色散效應抵消掉。這樣的補償受到非線性效應的限制,例如自相位調製
色散控制在超短脈衝 激光 中也十分重要。激光生成的總色散是評估激光脈衝的長度的重要因素。一對稜鏡 可用於生成淨負色散,從而用於抵消常用激光介質中的正色散。繞射光柵 亦可用於產生色散效應,並通常在高功率激光增幅系統中應用。
近年來,啁啾鏡
[ 編輯 ] 通過泰勒系數以微擾方式描述色散對於需要平衡來自多個不同系統的色散的優化問題是有利的。 例如,在啁啾脈衝激光放大器中,脈衝首先由展寬器及時展寬,以避免光學損傷。 然後在放大過程中,脈沖不可避免地累積通過材料的線性和非線性相位。 最後,脈沖在各種類型的壓縮器中被壓縮。 為了在累積階段取消任何剩餘的更高訂單,通常會測量和平衡單個訂單。 然而,對於統一系統,通常不需要這種擾動描述(即在波導中傳播)。
色散階已以計算友好的方式推廣,以 Lah-Laguerre 類型變換的形式。[ 6] [ 7]
色散階數由相位或波向量的泰勒展開式定義。
φ
(
ω
)
=
φ
|
ω
0
+
∂
φ
∂
ω
|
ω
0
(
ω
−
ω
0
)
+
1
2
∂
2
φ
∂
ω
2
|
ω
0
(
ω
−
ω
0
)
2
+
…
+
1
p
!
∂
p
φ
∂
ω
p
|
ω
0
(
ω
−
ω
0
)
p
+
…
{\displaystyle {\begin{array}{c}\varphi \mathrm {(} \omega \mathrm {)} =\varphi \left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial \varphi }{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}\varphi }{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}\varphi }{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}
k
(
ω
)
=
k
|
ω
0
+
∂
k
∂
ω
|
ω
0
(
ω
−
ω
0
)
+
1
2
∂
2
k
∂
ω
2
|
ω
0
(
ω
−
ω
0
)
2
+
…
+
1
p
!
∂
p
k
∂
ω
p
|
ω
0
(
ω
−
ω
0
)
p
+
…
{\displaystyle {\begin{array}{c}k\mathrm {(} \omega \mathrm {)} =k\left.\ \right|_{\omega _{0}}+\left.\ {\frac {\partial k}{\partial \omega }}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)+{\frac {1}{2}}\left.\ {\frac {\partial ^{2}k}{\partial \omega ^{2}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{2}\ +\ldots +{\frac {1}{p!}}\left.\ {\frac {\partial ^{p}k}{\partial \omega ^{p}}}\right|_{\omega _{0}}\left(\omega -\omega _{0}\right)^{p}+\ldots \end{array}}}
波子
k
(
ω
)
=
ω
c
n
(
ω
)
{\displaystyle k\mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}n\mathrm {(} \omega \mathrm {)} }
φ
(
ω
)
=
ω
c
O
P
(
ω
)
{\displaystyle \varphi \mathrm {(} \omega \mathrm {)} ={\frac {\omega }{c}}{\it {OP}}\mathrm {(} \omega \mathrm {)} }
∂
p
∂
ω
p
k
(
ω
)
=
1
c
(
p
∂
p
−
1
∂
ω
p
−
1
n
(
ω
)
+
ω
∂
p
∂
ω
p
n
(
ω
)
)
{\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}k\mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}n\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}n\mathrm {(} \omega \mathrm {)} \right)\ \end{array}}}
∂
p
∂
ω
p
φ
(
ω
)
=
1
c
(
p
∂
p
−
1
∂
ω
p
−
1
O
P
(
ω
)
+
ω
∂
p
∂
ω
p
O
P
(
ω
)
)
(
1
)
{\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}\varphi \mathrm {(} \omega \mathrm {)} ={\frac {1}{c}}\left(p{\frac {{\partial }^{p-1}}{\partial {\omega }^{p-1}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} +\omega {\frac {{\partial }^{p}}{\partial {\omega }^{p}}}{\it {OP}}\mathrm {(} \omega \mathrm {)} \right)\end{array}}(1)}
任何可微函數
f
(
ω
|
λ
)
{\displaystyle f\mathrm {(} \omega \mathrm {|} \lambda \mathrm {)} }
∂
p
∂
ω
p
f
(
ω
)
=
(
−
1
)
p
(
λ
2
π
c
)
p
∑
m
=
0
p
A
(
p
,
m
)
λ
m
∂
m
∂
λ
m
f
(
λ
)
{\displaystyle {\begin{array}{l}{\frac {\partial ^{p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}
,
{\displaystyle ,}
∂
p
∂
λ
p
f
(
λ
)
=
(
−
1
)
p
(
ω
2
π
c
)
p
∑
m
=
0
p
A
(
p
,
m
)
ω
m
∂
m
∂
ω
m
f
(
ω
)
(
2
)
{\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}(2)}
變換的矩陣元素是 Lah 系數:
A
(
p
,
m
)
=
p
!
(
p
−
m
)
!
m
!
(
p
−
1
)
!
(
m
−
1
)
!
{\displaystyle {\mathcal {A}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {1)!} }{\mathrm {(} m\mathrm {-} \mathrm {1)!} }}}
為 GDD 編寫的上述表達式表明,具有波長 GGD 的常數將具有零高階。 從 GDD 評估的更高階數是:
∂
p
∂
ω
p
G
D
D
(
ω
)
=
(
−
1
)
p
(
λ
2
π
c
)
p
∑
m
=
0
p
A
(
p
,
m
)
λ
m
∂
m
∂
λ
m
G
D
D
(
λ
)
{\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\omega }^{p}}}GDD\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}GDD\mathrm {(} \lambda \mathrm {)} }\end{array}}}
將表示為折射率
n
{\displaystyle n}
O
P
{\displaystyle OP}
p
t
h
{\displaystyle p^{th}}
P
O
D
=
d
p
φ
(
ω
)
d
ω
p
=
(
−
1
)
p
(
λ
2
π
c
)
(
p
−
1
)
∑
m
=
0
p
B
(
p
,
m
)
(
λ
)
m
d
m
O
P
(
λ
)
d
λ
m
{\displaystyle POD={\frac {d^{p}\varphi (\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}OP(\lambda )}{d\lambda ^{m}}}}
,
{\displaystyle ,}
P
O
D
=
d
p
k
(
ω
)
d
ω
p
=
(
−
1
)
p
(
λ
2
π
c
)
(
p
−
1
)
∑
m
=
0
p
B
(
p
,
m
)
(
λ
)
m
d
m
n
(
λ
)
d
λ
m
{\displaystyle POD={\frac {d^{p}k(\omega )}{d\omega ^{p}}}=(-1)^{p}({\frac {\lambda }{2\pi c}})^{(p-1)}\sum _{m=0}^{p}{\mathcal {B(p,m)}}(\lambda )^{m}{\frac {d^{m}n(\lambda )}{d\lambda ^{m}}}}
變換的矩陣元素是負 2 階的無符號拉蓋爾系數,給出如下:
B
(
p
,
m
)
=
p
!
(
p
−
m
)
!
m
!
(
p
−
2
)
!
(
m
−
2
)
!
{\displaystyle {\mathcal {B}}\mathrm {(} p,m\mathrm {)} ={\frac {p\mathrm {!} }{\left(p\mathrm {-} m\right)\mathrm {!} m\mathrm {!} }}{\frac {\mathrm {(} p\mathrm {-} \mathrm {2)!} }{\mathrm {(} m\mathrm {-} \mathrm {2)!} }}}
前十個色散階,明確地為波向量編寫,是:
G
D
=
∂
∂
ω
k
(
ω
)
=
1
c
(
n
(
ω
)
+
ω
∂
n
(
ω
)
∂
ω
)
=
1
c
(
n
(
λ
)
−
λ
∂
n
(
λ
)
∂
λ
)
=
v
g
r
−
1
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {GD}}}={\frac {\partial }{\partial \omega }}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \omega \mathrm {)} +\omega {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\frac {\mathrm {1} }{c}}\left(n\mathrm {(} \lambda \mathrm {)} -\lambda {\frac {\partial n\mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\right)=v_{gr}^{\mathrm {-} \mathrm {1} }\end{array}}}
群折射率
n
g
{\displaystyle n_{g}}
n
g
=
c
v
g
r
−
1
{\displaystyle n_{g}=cv_{gr}^{\mathrm {-} \mathrm {1} }}
G
D
D
=
∂
2
∂
ω
2
k
(
ω
)
=
1
c
(
2
∂
n
(
ω
)
∂
ω
+
ω
∂
2
n
(
ω
)
∂
ω
2
)
=
1
c
(
λ
2
π
c
)
(
λ
2
∂
2
n
(
λ
)
∂
λ
2
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {GDD}}}={\frac {{\partial }^{2}}{\partial {\omega }^{\mathrm {2} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {2} {\frac {\partial n\mathrm {(} \omega \mathrm {)} }{\partial \omega }}+\omega {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}\right)={\frac {\mathrm {1} }{c}}\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)\left({\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}
T
O
D
=
∂
3
∂
ω
3
k
(
ω
)
=
1
c
(
3
∂
2
n
(
ω
)
∂
ω
2
+
ω
∂
3
n
(
ω
)
∂
ω
3
)
=
−
1
c
(
λ
2
π
c
)
2
(
3
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
λ
3
∂
3
n
(
λ
)
∂
λ
3
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {TOD}}}={\frac {{\partial }^{3}}{\partial {\omega }^{\mathrm {3} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {3} {\frac {{\partial }^{2}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}+\omega {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }{\Bigl (}\mathrm {3} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}{\Bigr )}\end{array}}}
F
O
D
=
∂
4
∂
ω
4
k
(
ω
)
=
1
c
(
4
∂
3
n
(
ω
)
∂
ω
3
+
ω
∂
4
n
(
ω
)
∂
ω
4
)
=
1
c
(
λ
2
π
c
)
3
(
12
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
8
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
λ
4
∂
4
n
(
λ
)
∂
λ
4
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {FOD}}}={\frac {{\partial }^{4}}{\partial {\omega }^{\mathrm {4} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {4} {\frac {{\partial }^{3}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}+\omega {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }{\Bigl (}\mathrm {12} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {8} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}
F
i
O
D
=
∂
5
∂
ω
5
k
(
ω
)
=
1
c
(
5
∂
4
n
(
ω
)
∂
ω
4
+
ω
∂
5
n
(
ω
)
∂
ω
5
)
=
−
1
c
(
λ
2
π
c
)
4
(
60
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
60
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
15
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
λ
5
∂
5
n
(
λ
)
∂
λ
5
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {FiOD}}}={\frac {{\partial }^{5}}{\partial {\omega }^{\mathrm {5} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {5} {\frac {{\partial }^{4}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}+\omega {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {60} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {60} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {15} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}
S
i
O
D
=
∂
6
∂
ω
6
k
(
ω
)
=
1
c
(
6
∂
5
n
(
ω
)
∂
ω
5
+
ω
∂
6
n
(
ω
)
∂
ω
6
)
=
1
c
(
λ
2
π
c
)
5
(
360
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
480
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
180
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
24
λ
5
∂
5
n
(
λ
)
∂
λ
5
+
λ
6
∂
6
n
(
λ
)
∂
λ
6
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {SiOD}}}={\frac {{\partial }^{6}}{\partial {\omega }^{\mathrm {6} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {6} {\frac {{\partial }^{5}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}+\omega {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {360} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {480} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {180} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {24} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+{\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}
S
e
O
D
=
∂
7
∂
ω
7
k
(
ω
)
=
1
c
(
7
∂
6
n
(
ω
)
∂
ω
6
+
ω
∂
7
n
(
ω
)
∂
ω
7
)
=
−
1
c
(
λ
2
π
c
)
6
(
2520
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
4200
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
2100
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
420
λ
5
∂
5
n
(
λ
)
∂
λ
5
+
35
λ
6
∂
6
n
(
λ
)
∂
λ
6
+
λ
7
∂
7
n
(
λ
)
∂
λ
7
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {SeOD}}}={\frac {{\partial }^{7}}{\partial {\omega }^{\mathrm {7} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {7} {\frac {{\partial }^{6}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {6} }}}+\omega {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {2520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {2100} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {420} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {35} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}
E
O
D
=
∂
8
∂
ω
8
k
(
ω
)
=
1
c
(
8
∂
7
n
(
ω
)
∂
ω
7
+
ω
∂
8
n
(
ω
)
∂
ω
8
)
=
1
c
(
λ
2
π
c
)
7
(
20160
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
40320
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
25200
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
6720
λ
5
∂
5
n
(
λ
)
∂
λ
5
+
840
λ
6
∂
6
n
(
λ
)
∂
λ
6
+
+
48
λ
7
∂
7
n
(
λ
)
∂
λ
7
+
λ
8
∂
8
n
(
λ
)
∂
λ
8
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {EOD}}}={\frac {{\partial }^{8}}{\partial {\omega }^{\mathrm {8} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {8} {\frac {{\partial }^{7}n\mathrm {(} \omega \mathrm {)} }{{\partial \omega }^{\mathrm {7} }}}+\omega {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {20160} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {40320} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {25200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {6720} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {840} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {48} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+{\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}
N
O
D
=
∂
9
∂
ω
9
k
(
ω
)
=
1
c
(
9
∂
8
n
(
ω
)
∂
ω
8
+
ω
∂
9
n
(
ω
)
∂
ω
9
)
=
−
1
c
(
λ
2
π
c
)
8
(
181440
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
423360
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
317520
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
105840
λ
5
∂
5
n
(
λ
)
∂
λ
5
+
17640
λ
6
∂
6
n
(
λ
)
∂
λ
6
+
+
1512
λ
7
∂
7
n
(
λ
)
∂
λ
7
+
63
λ
8
∂
8
n
(
λ
)
∂
λ
8
+
λ
9
∂
9
n
(
λ
)
∂
λ
9
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {NOD}}}={\frac {{\partial }^{9}}{\partial {\omega }^{\mathrm {9} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {9} {\frac {{\partial }^{8}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}+\omega {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}\right)={-}{\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {181440} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {423360} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {317520} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {105840} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {17640} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {1512} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {63} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}
T
e
O
D
=
∂
10
∂
ω
10
k
(
ω
)
=
1
c
(
10
∂
9
n
(
ω
)
∂
ω
9
+
ω
∂
10
n
(
ω
)
∂
ω
10
)
=
1
c
(
λ
2
π
c
)
9
(
1814400
λ
2
∂
2
n
(
λ
)
∂
λ
2
+
4838400
λ
3
∂
3
n
(
λ
)
∂
λ
3
+
4233600
λ
4
∂
4
n
(
λ
)
∂
λ
4
+
1693440
λ
5
∂
5
n
(
λ
)
∂
λ
5
+
+
352800
λ
6
∂
6
n
(
λ
)
∂
λ
6
+
40320
λ
7
∂
7
n
(
λ
)
∂
λ
7
+
2520
λ
8
∂
8
n
(
λ
)
∂
λ
8
+
80
λ
9
∂
9
n
(
λ
)
∂
λ
9
+
λ
10
∂
10
n
(
λ
)
∂
λ
10
)
{\displaystyle {\begin{array}{l}{\boldsymbol {\it {TeOD}}}={\frac {{\partial }^{10}}{\partial {\omega }^{\mathrm {10} }}}k\mathrm {(} \omega \mathrm {)} ={\frac {\mathrm {1} }{c}}\left(\mathrm {10} {\frac {{\partial }^{9}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}+\omega {\frac {{\partial }^{10}n\mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}\right)={\frac {\mathrm {1} }{c}}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {1814400} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {4838400} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4233600} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{1693440}{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\\+\mathrm {352800} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {40320} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {2520} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {80} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}n\mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}
明確地,為相位
φ
{\displaystyle \varphi }
∂
p
∂
ω
p
f
(
ω
)
=
(
−
1
)
p
(
λ
2
π
c
)
p
∑
m
=
0
p
A
(
p
,
m
)
λ
m
∂
m
∂
λ
m
f
(
λ
)
{\displaystyle {\begin{array}{l}{\frac {\partial ^{p}}{\partial {\omega }^{p}}}f\mathrm {(} \omega \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\lambda }^{m}{\frac {{\partial }^{m}}{\partial {\lambda }^{m}}}f\mathrm {(} \lambda \mathrm {)} }\end{array}}}
,
{\displaystyle ,}
∂
p
∂
λ
p
f
(
λ
)
=
(
−
1
)
p
(
ω
2
π
c
)
p
∑
m
=
0
p
A
(
p
,
m
)
ω
m
∂
m
∂
ω
m
f
(
ω
)
{\displaystyle {\begin{array}{c}{\frac {{\partial }^{p}}{\partial {\lambda }^{p}}}f\mathrm {(} \lambda \mathrm {)} ={}{\left(\mathrm {-} \mathrm {1} \right)}^{p}{\left({\frac {\omega }{\mathrm {2} \pi c}}\right)}^{p}\sum \limits _{m={0}}^{p}{{\mathcal {A}}\mathrm {(} p,m\mathrm {)} {\omega }^{m}{\frac {{\partial }^{m}}{\partial {\omega }^{m}}}f\mathrm {(} \omega \mathrm {)} }\end{array}}}
∂
φ
(
ω
)
∂
ω
=
−
(
2
π
c
ω
2
)
∂
φ
(
ω
)
∂
λ
=
−
(
λ
2
2
π
c
)
∂
φ
(
λ
)
∂
λ
{\displaystyle {\begin{array}{l}{\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}={-}\left({\frac {\mathrm {2} \pi c}{{\omega }^{\mathrm {2} }}}\right){\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \lambda }}={-}\left({\frac {{\lambda }^{\mathrm {2} }}{\mathrm {2} \pi c}}\right){\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}\end{array}}}
∂
2
φ
(
ω
)
∂
ω
2
=
∂
∂
ω
(
∂
φ
(
ω
)
∂
ω
)
=
(
λ
2
π
c
)
2
(
2
λ
∂
φ
(
λ
)
∂
λ
+
λ
2
∂
2
φ
(
λ
)
∂
λ
2
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{2}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {2} }}}={\frac {\partial }{\partial \omega }}\left({\frac {\partial \varphi \mathrm {(} \omega \mathrm {)} }{\partial \omega }}\right)={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {2} }\left(\mathrm {2} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+{\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}\right)\end{array}}}
∂
3
φ
(
ω
)
∂
ω
3
=
−
(
λ
2
π
c
)
3
(
6
λ
∂
φ
(
λ
)
∂
λ
+
6
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
λ
3
∂
3
φ
(
λ
)
∂
λ
3
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{3}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {3} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {3} }\left(\mathrm {6} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {6} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+{\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}\right)\end{array}}}
∂
4
φ
(
ω
)
∂
ω
4
=
(
λ
2
π
c
)
4
(
24
λ
∂
φ
(
λ
)
∂
λ
+
36
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
12
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
λ
4
∂
4
φ
(
λ
)
∂
λ
4
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{4}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {4} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {4} }{\Bigl (}\mathrm {24} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {36} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+{\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}{\Bigr )}\end{array}}}
∂
5
φ
(
ω
)
∂
ω
5
=
−
(
λ
2
π
c
)
5
(
120
λ
∂
φ
(
λ
)
∂
λ
+
240
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
120
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
20
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
λ
5
∂
5
φ
(
λ
)
∂
λ
5
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{\mathrm {5} }\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {5} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {5} }{\Bigl (}\mathrm {120} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {240} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {20} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+{\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}{\Bigr )}\end{array}}}
∂
6
φ
(
ω
)
∂
ω
6
=
(
λ
2
π
c
)
6
(
720
λ
∂
φ
(
λ
)
∂
λ
+
1800
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
1200
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
300
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
30
λ
5
∂
5
φ
(
λ
)
∂
λ
5
+
λ
6
∂
6
φ
(
λ
)
∂
λ
6
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{6}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {6} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {6} }{\Bigl (}\mathrm {720} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1800} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1200} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {300} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {30} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}\mathrm {\ +} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}{\Bigr )}\end{array}}}
∂
7
φ
(
ω
)
∂
ω
7
=
−
(
λ
2
π
c
)
7
(
5040
λ
∂
φ
(
λ
)
∂
λ
+
15120
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
12600
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
4200
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
630
λ
5
∂
5
φ
(
λ
)
∂
λ
5
+
42
λ
6
∂
6
φ
(
λ
)
∂
λ
6
+
λ
7
∂
7
φ
(
λ
)
∂
λ
7
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{7}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {7} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {7} }{\Bigl (}\mathrm {5040} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {15120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {12600} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {4200} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {630} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {42} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+{\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}{\Bigr )}\end{array}}}
∂
8
φ
(
ω
)
∂
ω
8
=
(
λ
2
π
c
)
8
(
40320
λ
∂
φ
(
λ
)
∂
λ
+
141120
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
141120
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
58800
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
11760
λ
5
∂
5
φ
(
λ
)
∂
λ
5
+
1176
λ
6
∂
6
φ
(
λ
)
∂
λ
6
+
56
λ
7
∂
7
φ
(
λ
)
∂
λ
7
+
+
λ
8
∂
8
φ
(
λ
)
∂
λ
8
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{8}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {8} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {8} }{\Bigl (}\mathrm {40320} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {141120} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {141120} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {58800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {11760} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {1176} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\mathrm {56} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\\+{\lambda }^{\mathrm {8} }{\frac {\partial ^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}{\Bigr )}\end{array}}}
∂
9
φ
(
ω
)
∂
ω
9
=
−
(
λ
2
π
c
)
9
(
362880
λ
∂
φ
(
λ
)
∂
λ
+
1451520
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
1693440
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
846720
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
211680
λ
5
∂
5
φ
(
λ
)
∂
λ
5
+
28224
λ
6
∂
6
φ
(
λ
)
∂
λ
6
+
+
2016
λ
7
∂
7
φ
(
λ
)
∂
λ
7
+
72
λ
8
∂
8
φ
(
λ
)
∂
λ
8
+
λ
9
∂
9
φ
(
λ
)
∂
λ
9
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{9}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {9} }}}={-}{\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {9} }{\Bigl (}\mathrm {362880} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {1451520} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {1693440} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {846720} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {211680} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {28224} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {2016} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {72} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+{\lambda }^{\mathrm {9} }{\frac {\partial ^{\mathrm {9} }\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}{\Bigr )}\end{array}}}
∂
10
φ
(
ω
)
∂
ω
10
=
(
λ
2
π
c
)
10
(
3628800
λ
∂
φ
(
λ
)
∂
λ
+
16329600
λ
2
∂
2
φ
(
λ
)
∂
λ
2
+
21772800
λ
3
∂
3
φ
(
λ
)
∂
λ
3
+
12700800
λ
4
∂
4
φ
(
λ
)
∂
λ
4
+
3810240
λ
5
∂
5
φ
(
λ
)
∂
λ
5
+
635040
λ
6
∂
6
φ
(
λ
)
∂
λ
6
+
+
60480
λ
7
∂
7
φ
(
λ
)
∂
λ
7
+
3240
λ
8
∂
8
φ
(
λ
)
∂
λ
8
+
90
λ
9
∂
9
φ
(
λ
)
∂
λ
9
+
λ
10
∂
10
φ
(
λ
)
∂
λ
10
)
{\displaystyle {\begin{array}{l}{\frac {{\partial }^{10}\varphi \mathrm {(} \omega \mathrm {)} }{\partial {\omega }^{\mathrm {10} }}}={\left({\frac {\lambda }{\mathrm {2} \pi c}}\right)}^{\mathrm {10} }{\Bigl (}\mathrm {3628800} \lambda {\frac {\partial \varphi \mathrm {(} \lambda \mathrm {)} }{\partial \lambda }}+\mathrm {16329600} {\lambda }^{\mathrm {2} }{\frac {{\partial }^{2}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {2} }}}+\mathrm {21772800} {\lambda }^{\mathrm {3} }{\frac {{\partial }^{3}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {3} }}}+\mathrm {12700800} {\lambda }^{\mathrm {4} }{\frac {{\partial }^{4}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {4} }}}+\mathrm {3810240} {\lambda }^{\mathrm {5} }{\frac {{\partial }^{5}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {5} }}}+\mathrm {635040} {\lambda }^{\mathrm {6} }{\frac {{\partial }^{6}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {6} }}}+\\+\mathrm {60480} {\lambda }^{\mathrm {7} }{\frac {{\partial }^{7}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {7} }}}+\mathrm {3240} {\lambda }^{\mathrm {8} }{\frac {{\partial }^{8}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {8} }}}+\mathrm {90} {\lambda }^{\mathrm {9} }{\frac {{\partial }^{9}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {9} }}}+{\lambda }^{\mathrm {10} }{\frac {{\partial }^{10}\varphi \mathrm {(} \lambda \mathrm {)} }{\partial {\lambda }^{\mathrm {10} }}}{\Bigr )}\end{array}}}
在日光下使用一桶水和一片鏡子就可以觀察光的色散現象了。為了便於觀察現象,實驗中光路需要較大的出射角 來增大色散角度。此演示實驗中鏡子起到調整日光出射水面角度的作用。
^ 辞海网络版 - 色散 . www.cihai.com.cn. [2024-02-29 ] . (原始內容存檔 於2024-02-29). ^ 1882-1970., Born, Max,. Principles of optics : electromagnetic theory of propagation, interference and diffraction of light. 7th expanded. Cambridge: Cambridge University Press https://web.archive.org/web/20080620012317/http://www.worldcat.org/oclc/40200160 . 1999 [2019-01-28 ] . ISBN 0521642221OCLC 40200160 原始內容 存檔於2008-06-20). ^ Dispersion Compensation (頁面存檔備份 ,存於互聯網檔案館 ) Retrieved 25-08-2015.^ Born, M. and Wolf, E. (1980) "Principles of Optics, 6th ed." pg. 93. Pergamon Press.
^ Saleh, B.E.A. and Teich, M.C. Fundamentals of Photonics (2nd Edition) Wiley, 2007.
^ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio. Analytical Lah-Laguerre optical formalism for perturbative chromatic dispersion. Optics Express . 2022-10-24, 30 (22): 40779–40808. Bibcode:2022OExpr..3040779P PMID 36299007 doi:10.1364/OE.457139 (英語) . ^ Popmintchev, Dimitar; Wang, Siyang; Xiaoshi, Zhang; Stoev, Ventzislav; Popmintchev, Tenio. Theory of the Chromatic Dispersion, Revisited. 2020-08-30. arXiv:2011.00066 physics.optics ] (英語) .



 (英語).
(英語).
 [physics.optics] (英語).
[physics.optics] (英語).



















































