貪婪演算法

一般人唱散紙的時候也會應用到貪婪演算法。把$36換散︰$20 > $10 > $5 > $1

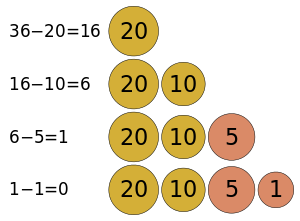
貪婪演算法（英語：greedy algorithm），又稱貪心演算法，是一種在每一步選擇中都採取在當前狀態下最好或最佳（即最有利）的選擇，從而希望導致結果是最好或最佳的演算法。比如在旅行推銷員問題中，如果旅行員每次都選擇最近的城市，那這就是一種貪婪演算法。

貪婪演算法在有最佳子結構的問題中尤為有效。最佳子結構的意思是局部最佳解能決定全域最佳解。簡單地說，問題能夠分解成子問題來解決，子問題的最佳解能遞推到最終問題的最佳解。

貪婪演算法與動態規劃的不同在於它對每個子問題的解決方案都做出選擇，不能回退。動態規劃則會儲存以前的運算結果，並根據以前的結果對當前進行選擇，有回退功能。

貪婪法可以解決一些最佳化問題，如：求圖中的最小生成樹、求哈夫曼編碼……對於其他問題，貪婪法一般不能得到我們所要求的答案。一旦一個問題可以通過貪婪法來解決，那麼貪婪法一般是解決這個問題的最好辦法。由於貪婪法的高效性以及其所求得的答案比較接近最佳結果，貪婪法也可以用作輔助演算法或者直接解決一些要求結果不特別精確的問題。在不同情況，選擇最優的解，可能會導致辛普森悖論（Simpson's Paradox），不一定出現最優的解。

貪婪演算法在數據科學領域被廣泛應用，特別是金融工程。其中一個貪婪演算法例子就是Ensemble method。

細節

1. 建立數學模型來描述問題。
2. 把求解的問題分成若干個子問題。
3. 對每一子問題求解，得到子問題的局部最佳解。
4. 把子問題的解局部最佳解合成原來解問題的一個解。

實現該演算法的過程：
從問題的某一初始解出發；while 能朝給定總目標前進一步 do，求出可行解的一個解元素；
最後，由所有解元素組合成問題的一個可行解。

應用

• 對於大部分的問題，貪婪法通常都不能找出最佳解（不過也有例外），因為他們一般沒有測試所有可能的解。貪婪法容易過早做決定，因而沒法達到最佳解。例如，所有對圖着色問題。
• 貪婪法在系統故障診斷策略生成乃至高校的排課系統中都可使用。

舉例

最小生成樹的演算法如Prim演算法、Kruskal演算法均為貪婪演算法，其中Prim演算法是對圖上的節點貪心，而Kruskal演算法是對圖上的邊貪心。

參見

• 動態規劃
• 最長公共子序列
• Floyd-Warshall演算法
• Viterbi演算法