极点分离

极点分离（Pole splitting）是在放大器电路中进行频率补偿时，可能会出现的现象。若在放大器的输入侧和输出侧加上电容器，希望将最低频率的极点（多半在输入侧）时，极点分离会使次低的极点频率提高。此极点的移动会提升放大器的稳定性，也会改善其阶跃响应，但其速度会变慢。

举例

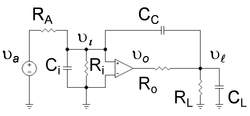
图1：在输入和输出之间有补偿电容器C_C的运算放大器。运算放大器有输入阻抗R_i和输出阻抗R_o

图2：用密勒定理转换后的电路，将辅偿电容转换为输入侧的密勒电容，以及输出侧随频率变化的电流源

这些例子可以看出在图1的运算放大器中加入电容器C_C，有两个目的：使得放大器最低频的极点频率再降低，并且将次低频率的极点频率提高。图1的放大器其低频的极点是因为加入的输入阻抗R_i以及电容C_i，其时间常数是C_i ( R_A || R_i )。因为密勒定理的缘故，此极点的频率会降低。此放大器有一个频率较高的极点，是因为负载电阻R_L和电容C_L，其时间常数是C_L ( R_o || R_L )。此极点的频率会因为密勒放大的补偿电容器C_C影响了输出电压分压器的频率相依关系，因此频率会提高。

第一个目的，也就是将最低频率极点的频率调低，可以用类似密勒效应条目中的作法。依照密勒定理中所述的程序，图1的电路可以转换为图2的电路，两者在电气上是等效的。将基尔霍夫电路定律应用在图2的输入侧，可以找到给理想运算放大器的电压是信号电压$\ v_{a}$的函数

${\frac {v_{i}}{v_{a}}}={\frac {R_{i}}{R_{i}+R_{A}}}{\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\ ,$

其滚降从频率f₁开始

${\begin{aligned}f_{1}&={\frac {1}{2\pi (C_{M}+C_{i})(R_{A}\|R_{i})}}\\&={\frac {1}{2\pi \tau _{1}}}\ ,\\\end{aligned}}$

其中的$\tau _{1}$是最低极点的时间常数，比原始的时间常数要低，原始的时间常数对应C_C = 0 F时，是${\frac {1}{2\pi C_{i}(R_{A}\|R_{i})}}$。

若考虑第二个目的，让较高频率的极点频率再往上增加，需要看电路的输出侧，输出侧为整体增益增加了第二个因子，也有额外的频率相依性，电压$\ v_{o}$是由理想放大器的增益决定的

$\ v_{o}=A_{v}v_{i}\ .$

利用这个关系，再在输出侧应用基尔霍夫电路定律，可以得到负载电压$v_{\ell }$相对于运算放大器输入电压$\ v_{i}$的函数：

${\frac {v_{\ell }}{v_{i}}}=A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\,\!$$\cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .$

这个运算式可以结合输入侧电路的增益，得到整体增益是

${\frac {v_{\ell }}{v_{a}}}={\frac {v_{\ell }}{v_{i}}}{\frac {v_{i}}{v_{a}}}$

$=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\,\!$$\cdot {\frac {1}{1+j\omega (C_{M}+C_{i})(R_{A}\|R_{i})}}\,\!$$\cdot {\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\ .$

增益公式中是一个单纯的二阶响应，有二个时间常数（其中也有一个零点，假设放大器增益A_v很大的话，此零点只有在很高频率才需要考虑，目前的讨论可以假设分子是1）。不过，虽然放大器看似二极的行为，但这二个时间常数比上述的要复杂，因为密勒电容中有藏着一个频率相依性，在较高频时就需要考虑。假设输出R-C乘积C_L ( R_o || R_L )，对应一个比低频极点频率要高很多的频率。那么密勒电容的值就不能用密勒近似的公式，需要用精确值。根据密勒定理，密勒电容为

${\begin{aligned}C_{M}&=C_{C}\left(1-{\frac {v_{\ell }}{v_{i}}}\right)\\&=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})}}\right)\ .\\\end{aligned}}$

（针对一个正的密勒电容，A_v为负值）。将此结果代入增益公式中，增益可以改写如下：

${\frac {v_{\ell }}{v_{a}}}=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}{\frac {R_{L}}{R_{L}+R_{o}}}{\frac {1+j\omega C_{C}R_{o}/A_{v}}{D_{\omega }}}\ ,$

其中D_ω是ω的二次式：

$D_{\omega }\,\!$ $=[1+j\omega (C_{L}+C_{C})(R_{o}\|R_{L})]\,\!$ $\cdot \ [1+j\omega C_{i}(R_{A}\|R_{i})]\,\!$ $\ +j\omega C_{C}(R_{A}\|R_{i})\,\!$ $\cdot \left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{O}}}\right)\,\!$ $\ +(j\omega )^{2}C_{C}C_{L}(R_{A}\|R_{i})(R_{O}\|R_{L})\ .$

上述的二次式可以改写如下：

$\ D_{\omega }=(1+j\omega {\tau }_{1})(1+j\omega {\tau }_{2})$

$=1+j\omega ({\tau }_{1}+{\tau }_{2}))+(j\omega )^{2}\tau _{1}\tau _{2}\ ,\$

其中$\tau _{1}$ and $\tau _{2}$是D_ω公式中结合了电阻和电容的值。。可以对应放大器二个极点的时间常数。其中一个是比较大，假设$\tau _{1}$是较大的时间常数，对应最低的极点，另外再假设$\tau _{1}$ >> $\tau _{2}$（若要有良好的阶跃响应，会需要$\tau _{1}$ >> $\tau _{2}$，可以看以下的如何选择C_C章节）

在放大器最低极点还低的频段，ω的线性项比二次项影响更大，因此D_ω的低频特性为：

${\begin{aligned}\ D_{\omega }&=1+j\omega [(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]\\&=1+j\omega (\tau _{1}+\tau _{2})\approx 1+j\omega \tau _{1}\ ,\ \\\end{aligned}}$

其中的C_M会用密勒效应重新定义为

$C_{M}=C_{C}\left(1-A_{v}{\frac {R_{L}}{R_{L}+R_{o}}}\right)\ ,$

就是之前低频计算的密勒电容。以此基础下，假设$\tau _{1}$ >> $\tau _{2}$，可以确定$\tau _{1}$。因为C_M很大，时间常数${\tau }_{1}$远大于其原始值C_i ( R_A || R_i ).

在高频时平方项影响较小，假设上述有关$\tau _{1}$ 的结果有效，对应较高频率的第二个时间常数，可以由D_ω的二次项求得，为

$\tau _{2}={\frac {\tau _{1}\tau _{2}}{\tau _{1}}}\approx {\frac {\tau _{1}\tau _{2}}{\tau _{1}+\tau _{2}}}\ .$

将平方项系数的公式代到$\tau _{1}\tau _{2}$，再加上 $\tau _{1}$的估计值，可以得到第二个极点的估计位置：

${\begin{aligned}\tau _{2}&={\frac {(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}{(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})}}\\&\approx {\frac {C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C}}{C_{M}}}(R_{O}\|R_{L})\ ,\\\end{aligned}}$

因为C_M很大，$\tau _{2}$会比原来的值C_L ( R_o || R_L )要小，也就是说，较高频率的极点其频率会因为C_C而提高.。

简单来说，导入C_C降低低频极点，提高高频极点。因此符合“极点分离”字面上的意思。

如何选择C_C

图3：二极点放大器设计的理想波德图。第一个极点在f₁，增益以20 dB / decade的斜率下降，第二点极点在f₂'，增益以40 dB / decade的斜率下降

在一般的应用中，传统放大器设计（称为“主极点”或“单极点补偿”）会要求放大器增益在转角频率处以20 dB/decade的斜率下降，降到0 dB增益，甚至更低 。在此设计下，放大器会稳定，而且有近乎最佳的阶跃响应，类似增益为1的电压缓冲器。而二极点补偿是更冒险的作法。

在设计中选择f₂的方式如图3所示。在最低极点f₁处，波德增益图开始以20 dB/decade的斜率下降。其目的是要维持20 dB/decade的下降斜率，一直到0dB为止，并且取20 log₁₀ A_v增益（以dB）表示的下降量，除以希望的频率变化（在log频率尺度上），( log₁₀ f₂  − log₁₀ f₁ ) = log₁₀ ( f₂ / f₁ ），就是这段的斜率

斜率 $=20{\frac {\mathrm {log_{10}} (A_{v})}{\mathrm {log_{10}} (f_{2}/f_{1})}}\ ,$

若f₂ = A_v f₁，上述的值会是是20 dB/decade。若f₂没有这么大，波德图的第二个转折会发生在增益降到0 dB之前，这会让稳定性变差，而且阶跃响应也会不好。

图3也说明了正确的增益和频率的关系，第二个极点至少要是第一个极点的A_v倍。此增益会因为放大器输入和输出的电压分配定则而减少一点，因此要修正输入和输出电压分配下的A_v，使用良好阶跃响应下的“极点—比例条件”（pole-ratio condition）可得：

${\frac {\tau _{1}}{\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,$

图4：用Microsoft Excel绘出低频率C_M的密勒电容C_M（上方）以及补偿电容C_C（下方） 和增益的函数关系，电容的单位是pF

利用上述时间常数的近似，可以得到

${\frac {\tau _{1}}{\tau _{2}}}\approx {\frac {(\tau _{1}+\tau _{2})^{2}}{\tau _{1}\tau _{2}}}\approx A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,$

或

${\frac {[(C_{M}+C_{i})(R_{A}\|R_{i})+(C_{L}+C_{C})(R_{o}\|R_{L})]^{2}}{(C_{C}C_{L}+C_{L}C_{i}+C_{i}C_{C})(R_{A}\|R_{i})(R_{O}\|R_{L})}}\,\!$ ${\color {White}\cdot }=A_{v}{\frac {R_{i}}{R_{i}+R_{A}}}\cdot {\frac {R_{L}}{R_{L}+R_{o}}}\ ,$

这是一个可以求得C_C近似值的二次式。图4是此式的图形。在低增益时放大器在没有补偿时就满足极点－增益条件（在图中低增益时的补偿电容器C_C很小），但增益增加时，因为需要的极点增益快速上升，补偿电容器就越来越重要（在图4时，补偿电容器随频率迅速的增加）。若增益更大时，因为C_C的密勒放大作用，会随着增益而增加（可以参考密勒方程式），因此必要的C_C会随着增益增加而减少。

若考虑设计的不确定性，保留较多的安全预度，A_v会设计成等式右边A_v值的两倍或三倍。可以参考Sansen或Huijsing的参考资料

回转率

上述都是小信号分析。不过若用在大信号时，因为补偿电容器需要充电和放电，会对放大器的回转率有不良的影响。而且因为需要为C_C充电，会限制斜坡函数输入下的响应。

相关条目

• 频率补偿
• 密勒效应
• 共源极
• 波德图
• 步阶响应
• CMOS放大器