超临界液气边界
超临界液气边界是三项图图中用于界定超临界流体更接近液体或更接近气体状态的线。这些线包括了费雪-维多姆线(Fisher–Widom line)、维多姆线(Widom line)和弗伦克尔线(Frenkel line)。
概述
[编辑]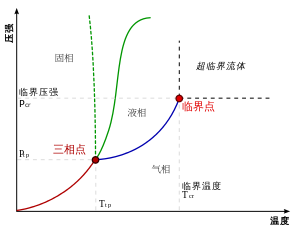
根据课本教授的内容,如果想要将液体在不经历相变的情况下转变为气体,我们可以将物质先加压再加热,绕过临界点进入超临界流体状态后再减压以获得气体。我们可以用不同的标准区分超临界流体更接近液态或更接近气态的状态。而这些标准可以让我们画出超临界流体的边界线。这些线不是从临界点出发,就是从略低于临界点的液-气边界(沸腾曲线)出发。这些边界曲线并不对应于一般的一阶相变或二阶相变,而是对应于较不严格的奇异点。
以下为几种用来区分超临界流体更接近液态还是更接近气态的方法:
费雪-维多姆线(Fisher–Widom line)[1]用来区分超临界流体的方法是借由径向分布函数在不同温度和压力下从单调渐近转变为振荡渐近的各个点,把这些点连起来就能得到费雪-维多姆线。
维多姆线(Widom line)是费雪-维多姆线(Fisher–Widom line)的概括,是由H.Eugene Stanley[2]命名。然而,是Jones和Walker[3]于1956年最先对维多姆线进行了实验测量,随后由Bernal于1964年将其命名为“超临界线”[4],并同时提出了流体结构上的解释。维多姆线的另一个评断标准是透过观察在固定压力下热容的峰值。[5][6]在临界点以下的区域,相变的线便是热容也就是潜热的峰值。在接近临界点时,潜热会下降至零,同时相变线附近纯相(液相和气相)的热容量也会逐渐地上升。在临界点上,潜热为零,但热容值大到变为奇异点。温度和压力超过临界点以后,热容量不再发散,而是出现平滑的峰值;该峰的最高点就是维多姆线。
弗伦克尔线(Frenkel line)是“刚性”和“非刚性”流体之间的边界,刚性则代表该物质更接近液态,非刚性则为气态。判断其非钢性的方法是观测该物质在特定情况下有无横波的出现。[7] 费伦克尔线是由这些从没有横波到有横波的转变点,每一点连起来得到的。上述转变点的评断标准之一是基于速度的自相关函数velocity autocorrelation function(简称vacf):在弗伦克尔线以下,vacf表现出振荡的行为,而在其上,vacf呈单调递减。第二个标准是在临界温度以下,液体可以维持其横向激发,而该横向激发会在液体加热的过程中消失。另一个标准是等容情况下热容的测量。靠近熔线的单原子液体每个原子的等容热容会接近(其中是玻尔兹曼常数)。横向激发的位能对热容的贡献为。因此根据液体热力学声子理论[8][9][10] 的直接预测,在横向激发消失的弗伦克尔线处,每个粒子的等容热容应为。
Anisimov等人(2004),[11]在没有参考Frenkel、Fisher或Widom的情况下,测量出了水在Tc(临界温度)以上100K超临界状态下的比热、膨胀系数、压缩性、黏度和声速,这些值的极值可以用密度的函数得出。
资料来源
[编辑]- ^ Fisher, Michael E.; Widom, Benjamin. Decay of Correlations in Linear Systems. The Journal of Chemical Physics (AIP Publishing). 1969, 50 (9): 3756–3772. Bibcode:1969JChPh..50.3756F. ISSN 0021-9606. doi:10.1063/1.1671624.
- ^ Boston University Research Briefs (2003), http://www.bu.edu/phpbin/researchbriefs/display.php?id=659
- ^ Jones, Gwyn Owain; Walker, P. A. Specific Heats of Fluid Argon near the Critical Point. Proceedings of the Physical Society B. 1956, 69 (12): 1348–1350. doi:10.1088/0370-1301/69/12/125.
- ^ Bernal, John Desmond. The Bakerian Lecture, 1962 The structure of liquids. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society). 1964-07-28, 280 (1382): 299–322. Bibcode:1964RSPSA.280..299B. ISSN 2053-9169. S2CID 178710030. doi:10.1098/rspa.1964.0147.
- ^ Simeoni, Giovanna Giulia; Bryk, Taras; Gorelli, Federico Aiace; Krisch, Michael; Ruocco, Giancarlo; Santoro, Mario; Scopigno, Tullio. The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nature Physics. 2010, 6 (7): 503–507. Bibcode:2010NatPh...6..503S. ISSN 1745-2473. doi:10.1038/nphys1683
 .
.
- ^ Banuti, Daniel. The Latent Heat of Supercritical Fluids. Periodica Polytechnica Chemical Engineering. 2019, 63 (2): 270–275. ISSN 1587-3765. doi:10.3311/PPch.12871
 .
.
- ^ Brazhkin, Vadim Veniaminovich; Fomin, Yury D.; Lyapin, Alexander G.; Ryzhov, Valentin N.; Trachenko, Kostya. Two liquid states of matter: A dynamic line on a phase diagram. Physical Review E (American Physical Society (APS)). 2012-03-30, 85 (3): 031203. Bibcode:2012PhRvE..85c1203B. ISSN 1539-3755. PMID 22587085. S2CID 544649. arXiv:1104.3414
 . doi:10.1103/physreve.85.031203.
. doi:10.1103/physreve.85.031203.
- ^ Bolmatov, Dima; Brazhkin, Vadim Veniaminovich; Trachenko, Kostya. The phonon theory of liquid thermodynamics. Scientific Reports. 2012-05-24, 2 (1): 421. Bibcode:2012NatSR...2E.421B. ISSN 2045-2322. PMC 3359528
 . PMID 22639729. arXiv:1202.0459
. PMID 22639729. arXiv:1202.0459  . doi:10.1038/srep00421
. doi:10.1038/srep00421  .
.
- ^ Bolmatov, Dima; Brazhkin, Vadim Veniaminovich; Trachenko, Kostya. Thermodynamic behaviour of supercritical matter. Nature Communications. 2013-08-16, 4 (1): 2331. Bibcode:2013NatCo...4.2331B. ISSN 2041-1723. PMID 23949085. arXiv:1303.3153
 . doi:10.1038/ncomms3331
. doi:10.1038/ncomms3331  .
.
- ^ "Phonon theory sheds light on liquid thermodynamics", PhysicsWorld, 2012
- ^ Anisimov, Mikhail A.; Sengers, Jan V.; Levelt Sengers, Johanna M. H.: Near-critical behavior of aqueous systems, chapter 2 in Aqueous Systems at Elevated Temperatures and Pressures, Palmer, Donald A.; Fernández-Prini, Roberto; Harvey, Allan H.; eds., Academic Press, 2004, pages 29-71, ISBN 978-0-125444-61-3, doi: 10.1016/B978-012544461-3/50003-X





