皮特里对偶
外观
在拓朴图论中,嵌入图的皮特里对偶(Petrie Dual)是指所有面皆为2-流形盘面之嵌入图的另一种嵌入,且是含有前述嵌入图之嵌入对象的皮特里多边形作为维面的图嵌入[1]。皮特里对偶亦可以作为一种多面体变换,称为皮特里变换(Petrie Operation),其会将原像的面以皮特里多边形做替换,然而变换结果通常会因为面转变为无法确定唯一封闭区域的皮特里多边形而导致体积与表面积不存在。[2]
性质
[编辑]皮特里对偶与一般的对偶变换一样,可做透过重复做两次相同变换使其变回原像[4]。而皮特里对偶与一般的对偶变换不同之处在于,一般的对偶变换是在同一个曲面上嵌入不同的图,而皮特里对偶是将相同图的嵌入在不同的曲面上。[1]
皮特里对偶与一般的对偶变换是威尔森变换的其中两种,且这些变换共同组成了一个群。[5]
正多面体的皮特里对偶
[编辑]对正多面体做皮特里变换可以得到正则地区图[3]。其变换结果会有g/2h个扭歪h边形,其中g为群的阶数、h为群的考克斯特数。举例来说,立方体的皮特里对偶是一个二分图,由4个[注 1]扭歪六边形组成,每个扭歪六边形环绕于立方体的赤道面上。在拓扑上,这个变换等同将图嵌入到环面上。[1]
凸正多面体的皮特里对偶列举如下[2]:
- 皮特里正四面体,施莱夫利符号{3,3}π,是正四面体经皮特里变换的结果,由3个正扭歪四边形组成,共有3个面、6条棱和4个顶点,其欧拉示性数χ为1,与立方体半形{4,3}/2拓朴同构[6]。
- 皮特里立方体,施莱夫利符号{4,3}π,是立方体经皮特里变换的结果,由4个正扭歪六边形组成,共有4个面、12条棱和8个顶点,其欧拉示性数χ为0[7]。 其也可以视为由4个正六边形镶嵌之面构成的环形多面体{6,3}(2,0)[9]。
- 皮特里正八面体,施莱夫利符号{3,4}π,是正八面体经皮特里变换的结果,由4个正扭歪六边形组成,共有4个面、12条棱和6个顶点,其欧拉示性数χ为−2[7],并存在有{6,4}3类型的四阶六边形双曲镶嵌之映射。[10]
- 皮特里正十二面体,施莱夫利符号{5,3}π,是正十二面体经皮特里变换的结果,由6个正扭歪十边形组成,共有6个面、32条棱和20个顶点,其欧拉示性数χ为-4[7],并存在有{10,3}5类型的正十边形双曲镶嵌之映射。[10]
- 皮特里正二十面体,施莱夫利符号{3,5}π,是正二十面体经皮特里变换的结果,由6个正扭歪十边形组成,共有6个面、32条棱和12个顶点,其欧拉示性数χ为-12[7],并存在有{10,5}3类型的五阶正十边形双曲镶嵌之映射。[10]
| 名称 | 皮特里正四面体 | 皮特里立方体 | 皮特里正八面体 | 皮特里正十二面体 | 皮特里正二十面体 |
|---|---|---|---|---|---|
| 施莱夫利符号 | {3,3}π , {4,3}3 | {4,3}π , {6,3}4 | {3,4}π , {6,4}3 | {5,3}π , {10,3} | {3,5}π , {10,5} |
| (顶点数,边数,面数), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| 面 | 3个正扭歪四边形
|
4个正扭歪六边形 | 6个正扭歪十边形 | ||

|

|

|

| ||
| 图像 | 
|

|

|

|

|
| 旋转动画 | 
|

|

|

|

|
| 相关图 |  {4,3}3 = {4,3}/2 = {4,3}(2,0) |
 {6,3}3 = {6,3}(2,0) |
 {6,4}3 = {6,4}(4,0) |
 {10,3}5 |
{10,5}3 |
非凸正多面体也有对应的皮特里对偶列举如下[2]:
| 名称 | 皮特里大十二面体 | 皮特里小星形十二面体 | 皮特里大二十面体 | 皮特里大星形十二面体 |
|---|---|---|---|---|
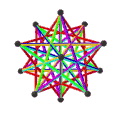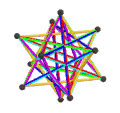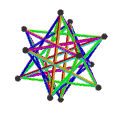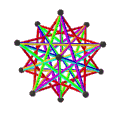
| 施莱夫利符号 | {5,5/2}π , {6,5/2} | {5/2,5}π , {6,5} | {3,5/2}π , {10/3,5/2} | {5/2,3}π , {10/3,3} |
| (顶点数,边数,面数), χ | (12,30,10), χ = -8 | (12,30,10), χ = -8 | (12,30,6), χ = -12 | (20,30,6), χ = -4 |
| 面 | 10个正扭歪六边形 | 6个正扭歪十边形 | ||

|

|

|
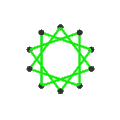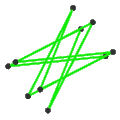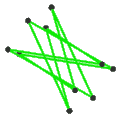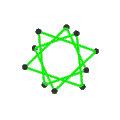
| |
| 图像 | 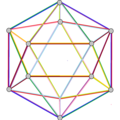
|

|

|

|
| 旋转动画 | 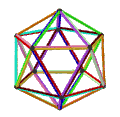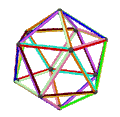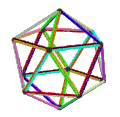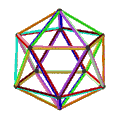
|
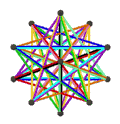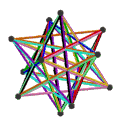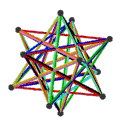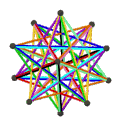
|
|

|
半正多面体的皮特里对偶
[编辑]| 名称 | 皮特里三角柱[10] | 皮特里截角四面体[10][7] | 皮特里截半立方体[10][7] |
|---|---|---|---|
| 原像 | 正三角柱 | 截角四面体 | 截半立方体 |
| (顶点数,边数,面数) | (6,9,3) | (12,18,3) | (12,24,6) |
| 面 | 3个扭歪六边形
|
3个扭歪十二边形
|
6个扭歪八边形
|
| 旋转动画 | 
|

|

|
注解
[编辑]参考文献
[编辑]- ^ 1.0 1.1 1.2 Gorini, Catherine A., Geometry at Work, MAA Notes 53, Cambridge University Press: 181, 2000, ISBN 9780883851647
- ^ 2.0 2.1 2.2 McMullen, P., Schulte, E. Regular Polytopes in Ordinary Space. Discrete & Computational Geometry. 1997/06/01, 17 (4): pp.449-478 [2020-08-09]. ISSN 1432-0444. doi:10.1007/PL00009304. (原始内容存档于2018-06-03).
- ^ 3.0 3.1 McMullen, Peter; Schulte, Egon, Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications 92, Cambridge University Press: 192, 2002, ISBN 9780521814966
- ^ Cunningham, Gabe. Self-dual, self-petrie covers of regular polyhedra. Symmetry (Molecular Diversity Preservation International). 2012, 4 (1): 208–218.
- ^ Jones, G. A.; Thornton, J. S., Operations on maps, and outer automorphisms, Journal of Combinatorial Theory, Series B, 1983, 35 (2): 93–103, MR 0733017, doi:10.1016/0095-8956(83)90065-5
- ^ Petrie Duals. weddslist.com. [2020-08-09]. (原始内容存档于2020-10-22).
- ^ 7.0 7.1 7.2 7.3 7.4 7.5 Deza, Michel and Dutour, Mathieu. Zigzag structure of complexes. arXiv preprint math/0405279. 2004.
- ^ Coxeter, H. S. M.; Moser, W. O. J., Generators and Relations for Discrete Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete 14 4th, Springer Verlag, 1980, ISBN 978-0-387-09212-6
- ^ Coxeter 1980[8], 8.4 Maps of type {3,6} or {6,3} on a torus.
- ^ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 Deza, Michel. Note on Petri duals and hypercube embeddings of semiregular polyhedra. Symmetry. 2011-01, 22.



