小世界網路
此條目的語調或風格或許不適合百科全書。 (2015年7月26日) |
在網路理論中,小世界網路是一類特殊的複雜網路結構,在這種網路中大部份的節點彼此並不相連,但絕大部份節點之間經過少數幾步就可到達。
在日常生活中,有時你會發現,某些你覺得與你隔得很「遙遠」的人,其實與你「很近」。小世界網路就是對這種現象(也稱為小世界現象)的數學描述。用數學中圖論的語言來說,小世界網路就是一個由大量頂點構成的圖,其中任意兩點之間的平均路徑長度比頂點數量小得多。除了社會人際網路以外,小世界網路的例子在生物學、物理學、電腦科學等領域也有出現。許多經驗中的圖可以由小世界網路來作為模型。全球資訊網、公路交通網、腦神經網路和基因網路都呈現小世界網路的特徵。
小世界網路最早是由鄧肯·瓦茨(Duncan Watts)和斯蒂文·斯特羅加茨(Steven Strogatz)在1998年引進的,將高集聚係數和低平均路徑長度作為特徵,提出了一種新的網路模型,一般就稱作瓦茨-斯特羅加茨模型(WS模型),這也是最典型的小世界網路的模型。
源起
[編輯]小世界網路的概念是隨著對複雜網路的研究而出現的。「網路」其實就是數學中圖論研究的圖,由一群頂點以及它們之間所連的邊構成。在網路理論中則換一套說法,用「節點」代替「頂點」,用「連結」代替「邊」。複雜網路的概念,是用來描述由大量節點以及這些節點之間錯綜複雜的聯絡所構成的網路。這樣的網路會出現在簡單網路中沒有的特殊拓撲特性。
自二十世紀60年代開始,對複雜網路的研究主要集中在隨機網路上。隨機網路,又稱隨機圖,是指通過隨機過程製造出的複雜網路。最典型的隨機網路是保羅·艾狄胥和阿爾弗雷德·雷尼提出的ER隨機圖。ER模型是基於一種「自然」的構造方法:假設有個節點,並假設每對節點之間相連的可能性都是常數。這樣構造出的網路就是ER模型網路。科學家們最初使用這種模型來解釋現實生活中的網路。
六度分隔理論
[編輯]最早觀察到小世界現象的是社會人際網路。將每個人作為節點,將人與人之間的人際關係(朋友,合作,相識等)作為連結,就建立起一個社會人際網路。有時你會發現,在這樣一個社會網路中,某些你覺得與你隔得很「遙遠」的人,其實與你「很近」:你很喜歡的一位知名作家的弟弟,其實是你舊時同班同學的男友;你跳槽到的新企業的總裁的侄子,會定期找你一個醫生朋友就醫;甚至和一個偶遇的陌生人聊天時,你發現你們都參加過某教授的講座,都認識某餐廳的老闆娘等等。你會感嘆:「這個世界真小。」對於世界上任意兩個人,通過這樣第三者、第四者的間接關係來建立聯絡的話,平均需要多少人呢?
二十世紀60年代,美國哈佛大學社會心理學家斯坦利·米爾格倫做了一個連鎖信實驗。他將一些信件交給自願的參加者,要求他們通過自己的熟人將信傳到信封上指明的收信人手裡,他發現,296封信件中有64封最終送到了目標人物手中。而在成功遞移的信件中,平均只需要5次轉發,就能夠到達目標。也就是說,在社會網路中,任意兩個人之間的「距離」是6[1]。這就是所謂的「六度分隔」理論。儘管他的實驗有不少缺陷,但這個現象引起了學界的注意。
凱文貝肯遊戲與艾狄胥數
[編輯]繼米爾格倫的實驗後,為了檢定六度分隔理論的真實性,人們又進行了一些其它實驗。其中一個著名的例子是「凱文·貝肯遊戲」(game of Kevin Bacon)。這個遊戲的主角是美國電影演員凱文·貝肯,遊戲的方法是通過不停地尋找共同出演同一電影的演員,最終「找到」另一個「目標」演員。遊戲裡每一個演員都有一個「貝肯數」:如果一個演員與貝肯合作過電影,那麼他(她)的「貝肯數」就是1。如果一個演員沒有與貝肯合作過,但與某個「貝肯數」為1的演員合作過,那麼他(她)的貝肯數」就是2,以此類推。比如說,吳彥祖在《80天環遊世界》中與盧克·威爾遜合作過,盧克·威爾遜在《家有跳狗》中與與貝肯合作過,所以吳彥祖的「貝肯數」是2[2]。對超過133萬名世界各地的演員的統計得出,他們平均的「貝肯數」是2.981[3],最大的也僅僅是8[4]。
一個類似的結果是數學界中的「艾狄胥數」。保羅·艾狄胥就是隨機圖理論的開創者之一,他是著名的數學家。與他一起發表過論文的學者的「艾狄胥數」是1,與這些學者合作發表過論文的學者的「艾狄胥數」是2,以此類推。美國數學會的資料庫中記錄的超過40萬名數學家們的「艾狄胥數」平均是4.65,最大的是13[5]。
定義
[編輯]米爾格倫實驗、凱文貝肯遊戲、艾狄胥數以及一些類似的實驗證明了,在現實世界裡的一些網路中,儘管節點數量龐大,但從一點出發,其實只需要經過僅僅幾步轉折,就能到達任一個節點。1998年,美國康奈爾大學的博士生鄧肯·瓦茨(Duncan Watts)和他的導師斯蒂文·斯特羅加茨(Steven Strogatz)發表了一篇名為《小世界網路的集體動力學》(Collective dynamics of the 'Small World' networks)的論文[6]。他們把這種現象歸類為某一類複雜網路的特性。他們注意到複雜網路可以按兩個獨立的結構特性分類,就是集聚係數和節點間的平均路徑長度。
平均路徑長度
[編輯]平均路徑長度也稱為特徵路徑長度或平均最短路徑長度,指的是一個網路中兩點之間最短路徑長度(或稱距離)的平均值。從一個節點出發,經過與它相連的節點,逐步「走」到另一個節點所經過的路途,稱為兩點間的路徑。其中最短的路徑也稱為兩點間的距離,記作。而平均路徑長度定義為:
這其中是節點數目,並定義節點到自身的最短路徑長度為0。如果不計算到自身的距離,那麼平均路徑長度的定義就變成[7]:
集聚係數
[編輯]集聚係數(也稱群聚係數、叢集係數)是用來描述圖或網路中的頂點(節點)之間結整合團的程度的係數。具體來說,是一個點的鄰接點之間相互連接的程度。例如在社群網路中,你的朋友之間相互認識的程度[8]。一個節點 的集聚係數 等於所有與它相連的頂點相互之間所連的邊的數量,除以這些頂點之間可以連出的最大邊數[9]。顯然 是一個介於0與1之間的數。 越接近1,表示這個節點附近的點越有「抱團」的趨勢。
介於隨機與規則之間
[編輯]對於純粹的規則網路,當其中連接數量接近飽和時,集聚係數很高,平均路徑長度也十分短。例如完全耦合網路(即完全圖),每兩個節點之間都相連,所以集聚係數是1,平均路徑長度是1。然而,現實中的複雜網路是稀疏的,連接的個數只是節點數的若干倍(),遠遠不到飽和。如果考慮將節點排列成正多邊形,每各節點都只與距離它最近的 個節點相連,那麼在比較大,但仍然保證時,其集聚係數為:
雖然能保持高集聚係數,但平均路徑長度為:
平均路徑長度與節點數成正比。
純粹的隨機網路(如ER隨機網路模型)有著很小的平均路徑長度,但同時集聚係數也很小。可是現實中的不少網路雖然有很小的平均路徑長度,但卻也有著比隨機網路高出相當多的集聚係數。因此瓦茨和斯特羅加茨認為,現實中的複雜網路是一種介於規則網路和隨機網路之間的網路。他們把這種特性稱為現實網路的小世界特性,就是:
瓦茨-斯特羅加茨模型
[編輯]在1998年的同一篇論文中,瓦茨和斯特羅加茨提出了一個模型來解釋小世界網路,後來被稱為瓦茨-斯特羅加茨模型(簡稱WS模型)。WS模型是基於兩人的一個假設:小世界模型是介於規則網路和隨機網路之間的網路。因此模型從一個完全的規則網路出發,以一定的機率將網路中的連接打亂重連。具體的構造如下:
- 首先從一個規則的網路開始。這個網路中的個節點排成正多邊形,每個節點都與離它最近的個節點相連。其中是一個遠小於的正整數。
- 選擇網路中的一個節點,從它開始(它自己是1號節點)將所有節點順時針編號,再將每個節點連出的連接也按順時針排序。然後,1號節點的第1條連接會有的機率被重連。重連方式如下:保持1號節點這一端不變,將連接的另一端隨機換成網路里的另一個節點,但不能使得兩個節點之間有多於1個連接。
- 重連之後,對2號、3號節點也做同樣的事(如果這其中有連接已經有過重連的機會,就不再重複),直到繞完一圈為止。
- 再次從1號節點的第2條連接開始,重複第2個步驟和第3個步驟,直到繞完一圈為止。
- 再次從1號節點開始,重複第4個步驟,直到所有的連接都被執行過第2個步驟(重連的步驟)。
由於個連接里每個連接都恰好有一次重連的機會,所以這個過程最後總會結束。最後得到的網路稱為WS模型網路[6][12]。
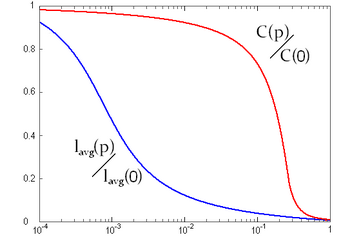
如果機率,那麼重連永遠不會發生,最後得到的是原來的規則網路。如果機率,那麼所有的連接都被重連了一次,最後得到的是一個完全的隨機網路。而對於機率的時候,瓦茨和斯特羅加茨考察了集聚係數和平均路徑長度與的關係,將這兩者看作是關於的函數:集聚係數,平均路徑長度[6]。他們發現,在從0變到1的過程中,下降得很快,而下降的比較慢。右側是演示這個關係的一個示意圖。圖中的橫軸是(使用對數坐標軸表示),縱軸是比值(介乎0與1之間)。藍色曲線表示與之比,紅色曲線表示與之比。從右圖可以看到,藍色曲線很快就逐漸下降到0.2以下,而紅色曲線則直到超過後才開始有顯著下降。當的時候,大概還有八成左右,但只占的不到百分之5了。所以對於很小的,可以很小,但可以很大。這正是小世界網路的特徵[6][13]。
更精確的計算[14]指出WS模型的集聚係數是:
而平均路徑長度則尚未有精確表達式[15]。
紐曼-瓦茨模型
[編輯]不久之後,瓦茨又與英國物理學家提出了另一個稍有不同的模型,稱為紐曼-瓦茨模型(NW模型)。其中將重連變成添加連結[16]。具體的構造方法是:第一步與WS模型相同,都是先建立一個規則網路;然後隨機選擇一對尚未連接的節點,設定有的機率產生連接。這樣重複一定次數,但不允許兩節點之間有多於一條連接,也不允許節點與自身相連。
紐曼-瓦茨模型在理論分析上比瓦茨-斯特羅加茨模型要簡單一點。當 很小而 很大的時候,這兩個模型本質上是一樣的[17]。
小世界網路的性質
[編輯]由於小世界網路具有高集聚係數,它的結構中不可避免地會有許多團(彼此之間兩兩相連的一小群節點)以及只比團差幾個連接的節點群。另一方面,任兩個結點大多會以至少一條短路徑連接著。這是要求有小的最短路徑長度平均值的結果。此外,小世界網路常連帶地具有一些性質,不過這些性質並不是作為這類網路非有不可的。很典型的是這類網路常常會出現「樞紐」(與很多節點都相連的節點)。
應用
[編輯]社會學的應用
[編輯]對於社會運動團體來說,小世界網路的優勢在於其由於使用高連接節點的過濾裝置而具有抗變化的能力,在將連接網路所需的鏈路數量降到最低的同時,其在資訊中轉方面也具有更好的效果。
小世界網路模型直接適用於以威廉-菲尼根為代表的社會學論點中的親和群體理論。親和群體是指以一個較大的目標或功能為承諾的小型半獨立的社會運動群體。雖然在節點層面上基本沒有親和力,但少數高連通性的成員卻發揮著連通性節點的功能,通過網路將不同群體聯絡起來。這種小世界模式已經被證明是一種極其有效的抗議組織策略,反對警察行動Clay Shirky認為,通過小世界網路建立的社會網路越大,網路內高連通性的節點就越有價值,親和力團體模式也是如此,每個團體內的少數人與外部團體相連,可以進行大量的動員和調整。威廉-芬尼根在提到1999年西雅圖WTO抗議活動時概述的通過親和群體建立的小世界網路就是一個實際的例子。
地球科學的應用
[編輯]地質學和地球物理學中研究的許多網路已被證明具有小世界網路的特徵。在斷裂系統和多孔物質中定義的網路已經證明了這些特徵.南加州地區的地震網路可能是一個小世界網路.上述例子發生在非常不同的空間尺度上,證明了地球科學中現象的尺度不變性. 氣候網路可以看作是小世界網路,其中各環節的長度尺度不同。
電腦的應用
[編輯]小世界網路已經被用來估計儲存在大型資料庫中的資訊的可用性。這種測量方法被稱為 "小世界資料轉換測量法"(Small World Data Transformation Measure),資料庫連結與小世界網路對齊的程度越高,使用者在未來提取資訊的可能性就越大。這種可用性通常是以能夠儲存在同一個庫中的資訊量為代價的。
Freenet對等網路已經在類比中被證明可以形成一個小世界網路,使得資訊的儲存和檢索可以隨著網路的增長而擴充效率。
大腦中的小世界神經網路
[編輯]大腦的解剖連接和皮質神經元的同步網路都表現出小世界拓撲結構。
小世界的神經元網路可以表現出短期記憶。Solla等人開發的電腦模型有兩個穩定的狀態,這種屬性(稱為雙穩態)被認為在記憶儲存中很重要。一個啟用脈衝在神經元之間產生了自我維持的通訊活動迴路。第二個脈衝結束這種活動。脈衝使系統在穩定的狀態之間切換:流動(記錄 "記憶")和靜止(保持記憶)。小世界神經元網路也被用作理解癲癇發作的模型。
在更普遍的層面上,大腦中許多大規模的神經網路,如視覺系統和腦幹,都表現出小世界的特性。
相關條目
[編輯]參考來源
[編輯]- ^ 《複雜網路理論及其應用》,第5頁
- ^ The Oracle of Bacon. Patrick Reynolds. [2011-07-12].
- ^ The Oracle of Bacon. Patrick Reynolds. [2011-07-12].
- ^ 《複雜網路理論及其應用》,第6頁
- ^ 《複雜網路理論及其應用》,第6-7頁
- ^ 6.0 6.1 6.2 6.3 Watts DJ, Strogatz SH. Collective dynamics of 'small-world' networks (PDF). Nature. June 1998, 393 (6684): 440–442 [2011-07-12]. Bibcode:1998Natur.393..440W. PMID 9623998. doi:10.1038/30918. (原始內容 (PDF)存檔於2007-04-18).
- ^ S.Boccaletti, 第182頁
- ^ 王冰、修志龍、唐煥文. 基于复杂网络理论的代谢网络结构研究进展 (PDF). 《中國生物工程雜誌》. 2005 No.6, 25–3: 10–14 [2011-07-11]. (原始內容 (PDF)存檔於2018-10-01).
- ^ 章忠志、榮莉莉、周濤. 一类无标度合作网络的演化模型 (PDF). 《系統工程理論與實踐》. 2005年11月, 11: 55–60 [2011-07-11]. (原始內容存檔 (PDF)於2018-09-29).
- ^ S.Boccaletti,第193頁
- ^ The structure and dynamics of networks, 第286頁
- ^ 《複雜網路與應用》第21頁
- ^ 《複雜網路與應用》第22頁
- ^ A. Barrat, M. Weigt. On the properties of small-world network models. The European Physical Journal B: 547–560. doi:10.1007/s100510050067.
- ^ 《複雜網路與應用》第23頁
- ^ M. E. J. Newman, D. J. Watts. Renormalization group analysis of the small-world network model. Phys. Lett. A: 341–346. doi:10.1016/S0375-9601(99)00757-4.
- ^ 《複雜網路理論及其應用》,第22頁
閱讀
[編輯]- 汪小帆,李翔,陳關榮. 《复杂网络理论及其应用》. 清華大學出版社. 2006. ISBN 9787302125051 (中文).
- 黃萍,張許傑,劉剛. 《小世界网络的研究现状与展望》. 情報雜誌 (中文).
- Mark E. J. Newman,Duncan J. Watts. The structure and dynamics of networks. Princeton University Press. 2006. ISBN 978-0691113579 (英語).
- Stefano Boccaletti, V. Latora, Y. Moreno, M. Chavez, D. Hwang. Complex networks: structure and dynamics. Volume 424, No 4-5 (2006.02). Elsevier Physics Report. doi:10.1016/j.physrep.2005.10.009 (英語).
- Richard Durrett. Random graph dynamics. Cambridge University Press. 2007. ISBN 978-0-521-86656-9 (英語).




























