掛在重力式摩天輪邊緣的乘客座艙在做平移運動。 運動學 (kinematics)是力學 的一門分支,專門描述物體的運動 ,即物體在空間 中的位置隨時間 的演進而作的改變,完全不考慮作用力 或質量 等等影響運動的因素。運動學與動力學 (dynamics)不同。動力學專門研究造成運動或影響運動的各種因素。動力學綜合運動學與力動學在一起,研究力學系統由於力的作用隨著時間演進而造成的運動。[ 1] [ 2]
在開始研討古典力學時,很自然地應該先思考各種可能的運動樣式,而暫時不將任何造成運動的因素納入考量。這初步探詢的知識就是運動學的學術領域。 — 愛德蒙·維特克, 質點與剛體分析動力學通論
任何一個物體,像是車子、火箭、星球等等,不論其尺寸大小,假若能夠忽略其內部的相對運動,假若其內部的每一部份都是朝相同的方向、以相同的速度移動,那麼,可以簡易地將此物體視為質點,將此物體的質心 的位置當作質點的位置 。在運動學裏,這種質點運動,不論是直線運動或是曲線運動,都是最基本的研究對象。
假若不能忽略物體內部的相對運動,則當解析其運動時,必須先將物體理想化為剛體 ,即一群彼此之間距離不變的質點。涉及剛體的問題比較困難。剛體可能會進行平移運動、旋轉運動 或兩者的綜合。更困難的案例是多剛體系統的運動。在這系統內,幾個剛體由四連桿組 的一部分。
質點運動學研究關於單獨質點的運動。從這方面得到的知識可以應用於研究質點動力學、一群質點的研究和其它力學領域。按照路徑的彎曲與否,質點運動可以分為直線運動與曲線運動。
在三維空間裏,詳細設定一個點P的位置需要完成三件事,找到參考點O(通常稱為原點 )、給出從點O到點P的距離、給出從點O到點P的直線方向;缺少其中任何資料,都會使得位置的描述不完全。[ 註 1]
將上述的資料數學化,用向量來描述位置。首先,為了要能夠一致地表示距離或方向,必須選擇一個三維坐標系,設定坐標系的原點O為參考點,以三維坐標系為參考系 。這樣,位置向量的大小就是點P離參考點的距離,而位置向量的方向就是從參考點到點P的直線方向。
質點的位置向量是從參考系的原點到質點的位置的向量。這向量表達了從原點到質點位置的距離和方向。在三維空間裏,點P的位置向量
r
{\displaystyle \mathbf {r} }
r
=
(
x
,
y
,
z
)
{\displaystyle \mathbf {r} =(x,y,z)}
其中,
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
位置向量
r
{\displaystyle \mathbf {r} }
|
r
|
=
x
2
+
y
2
+
z
2
{\displaystyle |\mathbf {r} |={\sqrt {x^{\ 2}+y^{\ 2}+z^{\ 2}}}}
從不同的參考系觀測點P的位置,可以得到不同的位置向量。
從某參考系觀測,假若質點的位置向量隨著時間的演進而改變,則稱此質點處於「移動狀態」;假若質點的位置向量保持不變,則稱此質點處於「靜止狀態」。請注意,不論是移動狀態或是靜止狀態,都依賴選擇的參考系而定。對於某參考系,處於靜止狀態的質點,對於另一個參考系,可能處於移動狀態。所以,移動狀態或靜止狀態都不是絕對的,都跟選擇的參考系有關。例如,假設在一輛移動中的火車內部有一位乘客。相對於火車,這乘客處於靜止狀態;但相對於火車外面的山嶺,這乘客處於移動狀態。
一個質點的移動「路徑」是從初始點移動到終極點所經過的軌跡。假設這初始點就是終結點,而移動時,其它每一個經過的點都只經過一次,則稱此路徑為「閉合迴路」。
路徑的樣子與參考系的選擇有關。對於某參考系,路徑可能是直線;對於另一個參考系,同樣的路徑可能是曲線。
位移向量與路徑距離之間的關係:位移向量的大小是距離的最小值 位移向量表達兩點之間位置的向量差。它可以表達一個質點在某時間間隔內由於運動而造成的位置改變。假設,點P的位置為
r
P
=
(
x
P
,
y
P
,
z
P
)
{\displaystyle \mathbf {r} _{P}=(x_{P},y_{P},z_{P})}
r
Q
=
(
x
Q
,
y
Q
,
z
Q
)
{\displaystyle \mathbf {r} _{Q}=(x_{Q},y_{Q},z_{Q})}
r
P
/
Q
{\displaystyle \mathbf {r} _{P/Q}}
r
P
/
Q
=
r
P
−
r
Q
=
(
x
P
−
x
Q
,
y
P
−
y
Q
,
z
P
−
z
Q
)
{\displaystyle \mathbf {r} _{P/Q}=\mathbf {r} _{P}-\mathbf {r} _{Q}=(x_{P}-x_{Q},y_{P}-y_{Q},z_{P}-z_{Q})}
位移向量的大小是點P與點Q之間的最短距離。位移向量與位置向量不同,位移向量不會因為選擇不同的參考系而改變。但是,在相對論裏,假設兩個參考系的相對速度不為零,則分別從這兩個參考系測量得到的位移向量也不相等。
距離是一種純量 ,表達一個質點從某一位置移動到另外一位置,所經過的路徑的長度。例如,一部跑車從初始點行駛到終結點,一共行駛了10公里距離的路程。但是,假若這路程是個閉合迴路,初始點與終結點相同,則這跑車的最終位移的大小(徑向距離)是0,這跑車最終回到了初始點。
假設質點的位置是時間的函數,
r
=
r
(
t
)
{\displaystyle \mathbf {r} =\mathbf {r} (t)}
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
s
{\displaystyle s}
s
=
∫
t
1
t
2
|
d
r
|
=
∫
t
1
t
2
d
s
=
∫
t
1
t
2
d
x
2
+
d
y
2
+
d
z
2
=
∫
t
1
t
2
(
d
x
d
t
)
2
+
(
d
y
d
t
)
2
+
(
d
z
d
t
)
2
d
t
{\displaystyle s=\int _{t_{1}}^{t_{2}}|\mathrm {d} \mathbf {r} |=\int _{t_{1}}^{t_{2}}\mathrm {d} s=\int _{t_{1}}^{t_{2}}{\sqrt {\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}}}=\int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {\mathrm {d} x}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} y}{\mathrm {d} t}}\right)^{2}+\left({\frac {\mathrm {d} z}{\mathrm {d} t}}\right)^{2}}}\;\mathrm {d} t}
這方程式應用到一個論據:在一段無窮小時間間隔內,位移的大小等於經過的路徑的長度。這論據類似於幾何論據:曲線的一段無窮小曲弧 與對應這曲弧的直弦 重疊在一起。
平均速度是在一段時間間隔內的速度的平均值,以方程式定義為
v
¯
=
Δ
r
Δ
t
{\displaystyle {\overline {\mathbf {v} }}={\frac {\Delta \mathbf {r} }{\Delta t}}}
其中,
v
¯
{\displaystyle {\overline {\mathbf {v} }}}
Δ
r
{\displaystyle \Delta \mathbf {r} }
Δ
t
{\displaystyle \Delta t}
由於時間間隔
Δ
t
{\displaystyle \Delta t}
v
¯
{\displaystyle {\overline {\mathbf {v} }}}
Δ
r
{\displaystyle \Delta \mathbf {r} }
速度是一種向量,表達隨著時間的演進而發生的位移改變。瞬時速度定義為,當
Δ
t
{\displaystyle \Delta t}
v
¯
{\displaystyle {\overline {\mathbf {v} }}}
Δ
r
{\displaystyle \Delta \mathbf {r} }
Δ
t
{\displaystyle \Delta t}
v
¯
{\displaystyle {\overline {\mathbf {v} }}}
v
{\displaystyle \mathbf {v} }
v
=
d
e
f
lim
Δ
t
→
0
Δ
r
Δ
t
=
d
r
d
t
{\displaystyle \mathbf {v} \ {\stackrel {def}{=}}\ \lim _{\Delta t\rightarrow 0}{\frac {\Delta \mathbf {r} }{\Delta t}}={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}}
以微分形式定義,速度是位移對於時間的導數。由於無窮小位移
d
r
{\displaystyle \mathrm {d} \mathbf {r} }
正切 於實際路徑,速度也正切於實際路徑。
速率
v
{\displaystyle v}
v
=
|
v
|
=
|
d
r
d
t
|
=
d
s
d
t
{\displaystyle v=|\mathbf {v} |=\left|{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right|={\frac {\mathrm {d} s}{\mathrm {d} t}}}
一個質點移動所經過的路徑距離是一種單調遞增 物理量。因此,
d
s
d
t
{\displaystyle {\frac {\mathrm {d} s}{\mathrm {d} t}}}
平均加速度是在一段時間間隔內的加速度的平均值,以方程式定義為
a
¯
=
Δ
v
Δ
t
{\displaystyle {\overline {\mathbf {a} }}={\frac {\Delta \mathbf {v} }{\Delta t}}}
其中,
a
¯
{\displaystyle {\overline {\mathbf {a} }}}
Δ
v
{\displaystyle \Delta \mathbf {v} }
Δ
t
{\displaystyle \Delta t}
加速度是一種表達質點移動速度隨著時間的演進而改變的向量。瞬時加速度定義為當
Δ
t
{\displaystyle \Delta t}
a
=
d
e
f
lim
Δ
t
→
0
Δ
v
Δ
t
=
d
v
d
t
{\displaystyle \mathbf {a} \ {\stackrel {def}{=}}\ \lim _{\Delta t\rightarrow 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}
以微分形式定義,加速度是速度對於時間的導數。
上述速度和加速度的定義式可以逆反過來,以積分形式表達為
v
(
t
)
=
v
0
+
∫
t
0
t
a
(
t
)
d
t
{\displaystyle \mathbf {v} (t)=\mathbf {v} _{0}+\int _{t_{0}}^{t}\mathbf {a} (t)\ \mathrm {d} t}
r
(
t
)
=
r
0
+
∫
t
0
t
v
(
t
)
d
t
=
r
0
+
v
0
t
+
∫
t
0
t
[
∫
t
0
t
a
(
t
)
d
t
]
d
t
{\displaystyle {\begin{aligned}\mathbf {r} (t)&=\mathbf {r} _{0}+\int _{t_{0}}^{t}\mathbf {v} (t)\ \mathrm {d} t\\&=\mathbf {r} _{0}+\mathbf {v} _{0}t+\int _{t_{0}}^{t}\left[\int _{t_{0}}^{t}\mathbf {a} (t)\mathrm {d} t\right]\ \mathrm {d} t\\\end{aligned}}}
; 其中,
t
0
{\displaystyle t_{0}}
v
0
{\displaystyle \mathbf {v} _{0}}
r
0
{\displaystyle \mathbf {r} _{0}}
假設,已知質點P、質點Q對於某參考點G的相對運動,應用向量代數 ,就可以描述質點P對於質點Q的相對運動。假設,從某參考系觀測,質點P、質點Q、參考點G的位置分別為
r
P
{\displaystyle \mathbf {r} _{P}}
r
Q
{\displaystyle \mathbf {r} _{Q}}
r
G
{\displaystyle \mathbf {r} _{G}}
r
P
/
G
=
r
P
−
r
G
{\displaystyle \mathbf {r} _{P/G}=\mathbf {r} _{P}-\mathbf {r} _{G}}
r
Q
/
G
=
r
Q
−
r
G
{\displaystyle \mathbf {r} _{Q/G}=\mathbf {r} _{Q}-\mathbf {r} _{G}}
質點P對於質點Q的相對位置為
r
P
/
Q
=
r
P
−
r
Q
=
r
P
−
r
G
−
r
Q
+
r
G
=
r
P
/
G
−
r
Q
/
G
{\displaystyle \mathbf {r} _{P/Q}=\mathbf {r} _{P}-\mathbf {r} _{Q}=\mathbf {r} _{P}-\mathbf {r} _{G}-\mathbf {r} _{Q}+\mathbf {r} _{G}=\mathbf {r} _{P/G}-\mathbf {r} _{Q/G}}
換句話說,質點P對於參考點G的相對位置為
r
P
/
G
=
r
P
/
Q
+
r
Q
/
G
{\displaystyle \mathbf {r} _{P/G}=\mathbf {r} _{P/Q}+\mathbf {r} _{Q/G}}
上述這些位移關係式,通過取時間導數,可以得到速度關係式:
v
P
/
Q
=
v
P
−
v
Q
{\displaystyle \mathbf {v} _{P/Q}=\mathbf {v} _{P}-\mathbf {v} _{Q}}
取時間導數於這些速度關係式,可以得到加速度關係式:
a
P
/
Q
=
a
P
−
a
Q
{\displaystyle \mathbf {a} _{P/Q}=\mathbf {a} _{P}-\mathbf {a} _{Q}}
特別注意,當速度接近光速 時,上述這些位移關係式或速度關係式並不正確,必須改用狹義相對論 推導出的關係式計算。
在直線運動中,質點沿著直線移動。如果將一個一維坐標系 的坐標軸放在這直線上,那麼,就可以用其坐標來設定位置 ,從而計算出速度 和加速度 等等。假設,在時間是
t
{\displaystyle t}
x
{\displaystyle x}
Δ
t
{\displaystyle \Delta t}
t
+
Δ
t
{\displaystyle t+\Delta t}
x
+
Δ
x
{\displaystyle x+\Delta x}
Δ
x
{\displaystyle \Delta x}
v
¯
{\displaystyle {\overline {v}}}
v
{\displaystyle v}
v
¯
=
Δ
x
Δ
t
{\displaystyle {\overline {v}}={\frac {\Delta x}{\Delta t}}}
v
=
lim
Δ
t
→
0
Δ
x
Δ
t
{\displaystyle v=\lim _{{\Delta t}\to 0}{\frac {\Delta x}{\Delta t}}}
質點P的平均加速度
a
¯
{\displaystyle {\overline {a}}}
a
{\displaystyle a}
a
¯
=
Δ
v
Δ
t
{\displaystyle {\overline {a}}={\frac {\Delta v}{\Delta t}}}
a
=
lim
Δ
t
→
0
Δ
v
Δ
t
{\displaystyle a=\lim _{{\Delta t}\to 0}{\frac {\Delta v}{\Delta t}}}
假設,質點P的位置是時間的函數
x
=
x
(
t
)
{\displaystyle x=x(t)}
v
(
t
)
=
d
x
d
t
{\displaystyle v(t)={\frac {\mathrm {d} x}{\mathrm {d} t}}}
a
(
t
)
=
d
v
d
t
=
d
2
x
d
t
2
{\displaystyle a(t)={\frac {\mathrm {d} v}{\mathrm {d} t}}={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}}
等速直線運動的加速度是零,速度
v
{\displaystyle v}
x
f
=
x
i
+
v
t
{\displaystyle x_{f}=x_{i}+vt}
其中,
x
i
{\displaystyle x_{i}}
x
f
{\displaystyle x_{f}}
等加速直線運動的加速度
a
{\displaystyle a}
x
f
−
x
i
=
v
i
t
+
1
2
a
t
2
{\displaystyle x_{f}-x_{i}=v_{i}t+{\frac {1}{2}}at^{2}}
x
f
−
x
i
=
1
2
(
v
f
+
v
i
)
t
{\displaystyle x_{f}-x_{i}={\frac {1}{2}}(v_{f}+v_{i})t}
v
f
=
v
i
+
a
t
{\displaystyle v_{f}=v_{i}+at}
v
f
2
=
v
i
2
+
2
a
(
x
f
−
x
i
)
{\displaystyle v_{f}^{2}=v_{i}^{2}+2a(x_{f}-x_{i})}
其中,
x
i
{\displaystyle x_{i}}
x
f
{\displaystyle x_{f}}
v
i
{\displaystyle v_{i}}
v
f
{\displaystyle v_{f}}
思考一個向上發射的物體;它將會往上直升,然後又落回到地面;它的軌跡全部都包含於同一條直線。假若認定朝上的方向為正值,那麼,這物體將會體驗到 -9.81m/s2 的等加速度。這物體的運動是等加速直線運動。
現在,請問幾個關於這運動的有趣的問題:這物體會在空中運動多久時間?在它開始往下落以前,它會升到多高?當它碰到地面時,它的最終速度是多少?輸入實際的數值,假設物體的最初速度是 +50 m/s。
它會在空中多久時間?
應用位移公式來計算時間:
x
f
=
x
i
+
v
i
t
+
1
2
a
t
2
{\displaystyle x_{f}=x_{i}+v_{i}t+{\frac {1}{2}}at^{2}}
因為這物體先飛離開地面,然後又落回到地面,淨位移是零:
0
=
v
i
t
+
1
2
a
t
2
=
t
(
v
i
+
1
2
a
t
)
{\displaystyle 0=v_{i}t+{\frac {1}{2}}at^{2}=t(v_{i}+{\frac {1}{2}}at)}
從這程式,可以求解到兩個答案。第一個答案是零;雖然這明顯解 是正確的答案;但是,它代表的時間間隔是那物體開始移動前的時間間隔。離開地面與回到地面所需要的時間為
t
=
−
2
v
i
a
=
−
2
∗
50
−
9.81
=
10.2
s
{\displaystyle t=-{\frac {2v_{i}}{a}}=-{\frac {2*50}{-9.81}}=10.2\ s}
在它開始往下落以前,它會飛到多高呢?
當這物體升到最高點的時候,它的速度是零。所以可以應用速度平方公式,
v
f
2
=
v
i
2
+
2
a
(
x
f
−
x
i
)
{\displaystyle v_{f}^{2}=v_{i}^{2}+2a(x_{f}-x_{i})}
假設以地面為座標系統的原點,那麼,
x
i
{\displaystyle x_{i}}
x
f
{\displaystyle x_{f}}
x
f
=
v
f
2
−
v
i
2
2
a
+
x
i
=
0
−
50
2
2
∗
−
9.81
+
0
=
127.55
m
{\displaystyle x_{f}={\frac {v_{f}^{2}-v_{i}^{2}}{2a}}+x_{i}={\frac {0-50^{2}}{2*-9.81}}+0=127.55\ m}
當它碰到地面時,它的最終速度會是多少?
正當這物體從最高點往回落的時候,它的速度是零。因此,可以同樣的用速度平方公式。帶進
x
i
{\displaystyle x_{i}}
v
f
=
v
i
2
+
2
a
(
x
f
−
x
i
)
=
0
2
+
2
(
−
9.81
)
(
0
−
127.55
)
=
50
m
/
s
{\displaystyle v_{f}={\sqrt {v_{i}^{2}+2a(x_{f}-x_{i})}}={\sqrt {0^{2}+2(-9.81)(0-127.55)}}=50\ m/s}
注意到初始速度與最終速度是等值的。這結果跟能量守恆定律 相符合。
質點隨時間演進而移動的曲線運動 定義質點在空間中沿著曲線的運動為「曲線運動」。曲線運動的位置、速度、加速度等等,皆須用向量 來表示。參考右圖,假設質點在時間
t
{\displaystyle t}
r
(
t
)
{\displaystyle \mathbf {r} (t)}
Δ
t
{\displaystyle \Delta t}
Δ
r
{\displaystyle \Delta \mathbf {r} }
r
(
t
+
Δ
t
)
{\displaystyle \mathbf {r} (t+\Delta t)}
v
=
lim
Δ
t
→
0
Δ
r
Δ
t
=
d
r
d
t
{\displaystyle \mathbf {v} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {r} }{\Delta t}}={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}}
在
Δ
t
→
0
{\displaystyle \Delta t\to 0}
正切 曲線於質點的位置。
定義速率 為速度的大小。假設這曲線從
r
{\displaystyle \mathbf {r} }
r
+
Δ
r
{\displaystyle \mathbf {r} +\Delta \mathbf {r} }
路徑 長度是
Δ
s
{\displaystyle \Delta s}
v
=
|
v
|
=
lim
Δ
t
→
0
Δ
s
Δ
t
=
d
s
d
t
{\displaystyle v={\begin{vmatrix}\mathbf {v} \end{vmatrix}}=\lim _{{\Delta t}\to 0}{\frac {\Delta s}{\Delta t}}={\frac {\mathrm {d} s}{\mathrm {d} t}}}
假設質點在間隔
Δ
t
{\displaystyle \Delta t}
Δ
v
{\displaystyle \Delta \mathbf {v} }
a
=
lim
Δ
t
→
0
Δ
v
Δ
t
=
d
v
d
t
{\displaystyle \mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}}
求解曲線運動問題時,選擇合適的坐標系是一項非常重要的步驟。運動所遭遇到的約束、或作用力的幾何特性,往往是決定合適坐標的主要因素。假設,限制一粒串珠只能繞圓環移動,那麼,以圓心 為頂點 ,包含串珠與圓環的另一點的角 ,其角弧 可能是合適的坐標。類似地,假設施加於質點的作用力是連心力 ,則合適的坐標系可能是極坐標系 。
直角坐標系。x-軸的方向是親近讀者。 三維空間的直角坐標系有三個坐標軸:x-軸、y-軸、z-軸。採用直角坐標系,位置、速度、加速度表示為
r
=
x
x
^
+
y
y
^
+
z
z
^
{\displaystyle \mathbf {r} =x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}
v
=
v
x
x
^
+
v
y
y
^
+
v
z
z
^
{\displaystyle \mathbf {v} =v_{x}{\hat {\mathbf {x} }}+v_{y}{\hat {\mathbf {y} }}+v_{z}{\hat {\mathbf {z} }}}
a
=
a
x
x
^
+
a
y
y
^
+
a
z
z
^
{\displaystyle \mathbf {a} =a_{x}{\hat {\mathbf {x} }}+a_{y}{\hat {\mathbf {y} }}+a_{z}{\hat {\mathbf {z} }}}
其中,
x
{\displaystyle x}
y
{\displaystyle y}
z
{\displaystyle z}
v
x
=
d
x
d
t
,
v
y
=
d
y
d
t
,
v
z
=
d
z
d
t
{\displaystyle v_{x}={\frac {\mathrm {d} x}{\mathrm {d} t}}\ \ ,\qquad \qquad v_{y}={\frac {\mathrm {d} y}{\mathrm {d} t}}\ \ ,\qquad \qquad v_{z}={\frac {\mathrm {d} z}{\mathrm {d} t}}}
a
x
=
d
v
x
d
t
,
a
y
=
d
v
y
d
t
,
a
z
=
d
v
z
d
t
{\displaystyle a_{x}={\frac {\mathrm {d} v_{x}}{\mathrm {d} t}}\ ,\qquad \qquad a_{y}={\frac {\mathrm {d} v_{y}}{\mathrm {d} t}}\ ,\qquad \qquad a_{z}={\frac {\mathrm {d} v_{z}}{\mathrm {d} t}}}
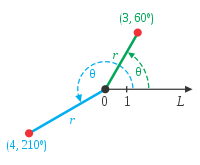
在極點為O、極軸為L的極坐標系裏,點
(
3
,
60
∘
)
{\displaystyle (3,60^{\circ })}
(
4
,
210
∘
)
{\displaystyle (4,210^{\circ })}
在二維空間裡,極坐標系用半徑坐標
r
{\displaystyle r}
θ
{\displaystyle \theta }
r
=
r
r
^
{\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}
v
=
r
˙
r
^
+
r
θ
˙
θ
^
{\displaystyle \mathbf {v} ={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\hat {\boldsymbol {\theta }}}}
a
=
(
r
¨
−
r
θ
˙
2
)
r
^
+
(
r
θ
¨
+
2
r
˙
θ
˙
)
θ
^
{\displaystyle \mathbf {a} =({\ddot {r}}-r{\dot {\theta }}^{2}){\hat {\mathbf {r} }}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\hat {\boldsymbol {\theta }}}}
其中,
r
^
{\displaystyle {\hat {\mathbf {r} }}}
θ
^
{\displaystyle {\hat {\boldsymbol {\theta }}}}
質點的「角位置」就是它的角坐標
θ
{\displaystyle \theta }
Δ
θ
{\displaystyle \Delta \theta }
角速度 的大小
ω
{\displaystyle \omega }
ω
=
θ
˙
{\displaystyle \omega ={\dot {\theta }}}
角加速度 的大小
α
{\displaystyle \alpha }
α
=
ω
˙
=
θ
¨
{\displaystyle \alpha ={\dot {\omega }}={\ddot {\theta }}}
類似等加速直線運動,假設曲線運動的角加速度
α
{\displaystyle \alpha }
θ
f
−
θ
i
=
ω
i
t
+
1
2
α
t
2
{\displaystyle \theta _{f}-\theta _{i}=\omega _{i}t+{\frac {1}{2}}\alpha t^{2}}
θ
f
−
θ
i
=
1
2
(
ω
f
+
ω
i
)
t
{\displaystyle \theta _{f}-\theta _{i}={\frac {1}{2}}(\omega _{f}+\omega _{i})t}
ω
f
=
ω
i
+
α
t
{\displaystyle \omega _{f}=\omega _{i}+\alpha t}
ω
f
2
=
ω
i
2
+
2
α
(
θ
f
−
θ
i
)
{\displaystyle \omega _{f}^{2}=\omega _{i}^{2}+2\alpha (\theta _{f}-\theta _{i})}
其中,
θ
i
{\displaystyle \theta _{i}}
θ
f
{\displaystyle \theta _{f}}
ω
i
{\displaystyle \omega _{i}}
ω
f
{\displaystyle \omega _{f}}
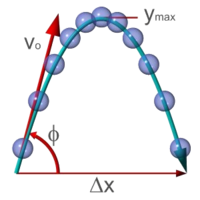
如果一個物體不是垂直向上發射,而是與地平面呈
Φ
{\displaystyle \Phi }
v
0
=
50
m
/
s
{\displaystyle v_{0}=50m/s}
Φ
=
30
∘
{\displaystyle \Phi =30^{\circ }}
請問在碰到地面以前,它會在空中飛行多遠?
垂直方向,這物體會感覺到
−
9.81
m
/
s
2
{\displaystyle -9.81m/s^{2}}
Δ
x
=
x
f
−
x
i
=
v
i
cos
(
Φ
)
t
+
1
2
a
t
2
=
v
i
cos
(
Φ
)
t
{\displaystyle \Delta x=x_{f}-x_{i}=v_{i}\cos(\Phi )\ t+{\frac {1}{2}}at^{2}=v_{i}\cos(\Phi )\ t}
為要解答這問題,必須找到
t
{\displaystyle t}
t
{\displaystyle t}
0
=
v
i
sin
(
Φ
)
t
+
1
2
a
t
2
=
t
(
v
i
sin
(
Φ
)
+
1
2
a
t
)
{\displaystyle 0=v_{i}\sin(\Phi )\ t+{\frac {1}{2}}at^{2}=t(v_{i}\sin(\Phi )+{\frac {1}{2}}at)}
現在求解
t
{\displaystyle t}
Δ
x
=
v
i
cos
(
Φ
)
(
−
2
v
i
sin
(
Φ
)
a
)
=
−
v
i
2
sin
2
(
Φ
)
a
=
220.70
m
{\displaystyle \Delta x=v_{i}\cos(\Phi )\left({\frac {-2v_{i}\sin(\Phi )}{a}}\right)=-{\frac {v_{i}^{2}\sin 2(\Phi )}{a}}=220.70\ m}
在三維空間內,設定兩個參考系:空間參考系S與旋轉參考系R。空間參考系S的標準正交基 為
x
^
{\displaystyle {\hat {\mathbf {x} }}}
y
^
{\displaystyle {\hat {\mathbf {y} }}}
z
^
{\displaystyle {\hat {\mathbf {z} }}}
標準正交基 為
e
^
x
{\displaystyle {\hat {\mathbf {e} }}_{x}}
e
^
y
{\displaystyle {\hat {\mathbf {e} }}_{y}}
e
^
z
{\displaystyle {\hat {\mathbf {e} }}_{z}}
原點 共點。空間參考系S靜止不動,旋轉參考系R繞著固定軸
z
^
=
e
^
z
{\displaystyle {\hat {\mathbf {z} }}={\hat {\mathbf {e} }}_{z}}
x
^
{\displaystyle {\hat {\mathbf {x} }}}
y
^
{\displaystyle {\hat {\mathbf {y} }}}
e
^
x
{\displaystyle {\hat {\mathbf {e} }}_{x}}
e
^
y
{\displaystyle {\hat {\mathbf {e} }}_{y}}
當計算質點的位置、速度、加速度之時,必須特別注意到旋轉參考系R是在持續地旋轉,單位向量
e
^
x
{\displaystyle {\hat {\mathbf {e} }}_{x}}
e
^
y
{\displaystyle {\hat {\mathbf {e} }}_{y}}
e
^
x
{\displaystyle {\hat {\mathbf {e} }}_{x}}
e
^
y
{\displaystyle {\hat {\mathbf {e} }}_{y}}
ω
=
ω
z
^
{\displaystyle {\boldsymbol {\omega }}=\omega {\hat {z}}}
z
^
{\displaystyle {\hat {z}}}
t
=
0
{\displaystyle t=0}
e
^
x
=
x
^
{\displaystyle {\hat {\mathbf {e} }}_{x}={\hat {\mathbf {x} }}}
e
^
y
=
y
^
{\displaystyle {\hat {\mathbf {e} }}_{y}={\hat {\mathbf {y} }}}
則在時間
t
{\displaystyle t}
e
^
x
=
cos
(
ω
t
)
x
^
+
sin
(
ω
t
)
y
^
{\displaystyle {\hat {\mathbf {e} }}_{x}=\cos(\omega t){\hat {\mathbf {x} }}+\sin(\omega t){\hat {\mathbf {y} }}}
e
^
y
=
−
sin
(
ω
t
)
x
^
+
cos
(
ω
t
)
y
^
{\displaystyle {\hat {\mathbf {e} }}_{y}=-\sin(\omega t){\hat {\mathbf {x} }}+\cos(\omega t){\hat {\mathbf {y} }}}
兩個單位向量
e
^
x
{\displaystyle {\hat {\mathbf {e} }}_{x}}
e
^
y
{\displaystyle {\hat {\mathbf {e} }}_{y}}
d
e
^
x
d
t
=
−
ω
sin
(
ω
t
)
x
^
+
ω
cos
(
ω
t
)
y
^
=
ω
e
^
y
{\displaystyle {\frac {\mathrm {d} {\hat {\mathbf {e} }}_{x}}{\mathrm {d} t}}=-\omega \sin(\omega t){\hat {\mathbf {x} }}+\omega \cos(\omega t){\hat {\mathbf {y} }}=\omega {\hat {\mathbf {e} }}_{y}}
d
e
^
y
d
t
=
−
ω
cos
(
ω
t
)
x
^
−
ω
sin
(
ω
t
)
y
^
=
−
ω
e
^
x
{\displaystyle {\frac {\mathrm {d} {\hat {\mathbf {e} }}_{y}}{\mathrm {d} t}}=-\omega \cos(\omega t){\hat {\mathbf {x} }}-\omega \sin(\omega t){\hat {\mathbf {y} }}=-\omega {\hat {\mathbf {e} }}_{x}}
對於含時向量
F
(
t
)
=
f
x
x
^
+
f
y
y
^
=
F
x
e
^
x
+
F
y
e
^
y
{\displaystyle \mathbf {F} (t)=f_{x}{\hat {x}}+f_{y}{\hat {y}}=F_{x}{\hat {\mathbf {e} }}_{x}+F_{y}{\hat {\mathbf {e} }}_{y}}
(
d
F
d
t
)
=
f
˙
x
x
^
+
f
˙
y
y
^
=
F
˙
x
e
^
x
+
F
˙
y
e
^
y
+
F
x
(
d
e
^
x
d
t
)
+
F
y
(
d
e
^
y
d
t
)
=
F
˙
x
e
^
x
+
F
˙
y
e
^
y
+
F
x
ω
e
^
y
−
F
y
ω
e
^
x
=
F
˙
x
e
^
x
+
F
˙
y
e
^
y
+
ω
×
F
{\displaystyle {\begin{aligned}\left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)&={\dot {f}}_{x}{\hat {\mathbf {x} }}+{\dot {f}}_{y}{\hat {\mathbf {y} }}\\&={\dot {F}}_{x}{\hat {\mathbf {e} }}_{x}+{\dot {F}}_{y}{\hat {\mathbf {e} }}_{y}+F_{x}\left({\frac {\mathrm {d} {\hat {\mathbf {e} }}_{x}}{\mathrm {d} t}}\right)+F_{y}\left({\frac {\mathrm {d} {\hat {\mathbf {e} }}_{y}}{\mathrm {d} t}}\right)\\&={\dot {F}}_{x}{\hat {\mathbf {e} }}_{x}+{\dot {F}}_{y}{\hat {\mathbf {e} }}_{y}+F_{x}\omega {\hat {\mathbf {e} }}_{y}-F_{y}\omega {\hat {\mathbf {e} }}_{x}\\&={\dot {F}}_{x}{\hat {\mathbf {e} }}_{x}+{\dot {F}}_{y}{\hat {\mathbf {e} }}_{y}+{\boldsymbol {\omega }}\times \mathbf {F} \\\end{aligned}}}
。 設定
(
d
F
d
t
)
s
p
a
c
e
=
f
˙
x
x
^
+
f
˙
y
y
^
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }={\dot {f}}_{x}{\hat {\mathbf {x} }}+{\dot {f}}_{y}{\hat {\mathbf {y} }}}
(
d
F
d
t
)
r
o
t
a
t
e
=
F
˙
x
e
^
x
+
F
˙
y
e
^
y
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }={\dot {F}}_{x}{\hat {\mathbf {e} }}_{x}+{\dot {F}}_{y}{\hat {\mathbf {e} }}_{y}}
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
F
d
t
)
s
p
a
c
e
=
(
d
F
d
t
)
r
o
t
a
t
e
+
ω
×
F
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }+{\boldsymbol {\omega }}\times \mathbf {F} }
這方程式的叉積項目可以這樣理解:假設向量
F
{\displaystyle \mathbf {F} }
F
{\displaystyle \mathbf {F} }
ω
{\displaystyle {\boldsymbol {\omega }}}
z
^
{\displaystyle {\hat {\mathbf {z} }}}
F
{\displaystyle \mathbf {F} }
ω
×
F
{\displaystyle {\boldsymbol {\omega }}\times \mathbf {F} }
向量
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
d
t
)
s
p
a
c
e
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }}
(
d
d
t
)
r
o
t
a
t
e
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }}
(
d
d
t
)
s
p
a
c
e
=
(
d
d
t
)
r
o
t
a
t
e
+
ω
×
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }+{\boldsymbol {\omega }}\times }
假設,從空間參考系S觀測,質點P的位置為
r
=
x
S
x
^
+
y
S
y
^
{\displaystyle \mathbf {r} =x_{S}\ {\hat {\mathbf {x} }}+y_{S}\ {\hat {\mathbf {y} }}}
而從旋轉參考系R觀測,同一質點P的位置為
r
=
x
R
e
^
x
+
y
R
e
^
y
{\displaystyle \mathbf {r} =x_{R}\ {\hat {\mathbf {e} }}_{x}+y_{R}\ {\hat {\mathbf {e} }}_{y}}
從空間參考系S觀測,質點P的速度
v
=
x
˙
S
x
^
+
y
˙
S
y
^
{\displaystyle \mathbf {v} ={\dot {x}}_{S}\ {\hat {\mathbf {x} }}+{\dot {y}}_{S}\ {\hat {\mathbf {y} }}}
v
=
d
e
f
(
d
r
d
t
)
s
p
a
c
e
=
(
d
r
d
t
)
r
o
t
a
t
e
+
ω
×
r
=
v
R
+
ω
×
r
{\displaystyle \mathbf {v} \ {\stackrel {def}{=}}\ \left({\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }+{\boldsymbol {\omega }}\times \mathbf {r} =\mathbf {v} _{R}+{\boldsymbol {\omega }}\times \mathbf {r} }
其中,
v
R
=
d
e
f
(
d
r
d
t
)
r
o
t
a
t
e
=
x
˙
R
e
^
x
+
y
˙
R
e
^
y
{\displaystyle \mathbf {v} _{R}\ {\stackrel {def}{=}}\ \left({\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right)_{\mathrm {rotate} }={\dot {x}}_{R}\ {\hat {\mathbf {e} }}_{x}+{\dot {y}}_{R}\ {\hat {\mathbf {e} }}_{y}}
質點P的加速度為
a
=
d
e
f
(
d
v
d
t
)
s
p
a
c
e
=
(
d
v
R
d
t
)
s
p
a
c
e
+
(
d
(
ω
×
r
)
d
t
)
s
p
a
c
e
=
(
d
v
R
d
t
)
s
p
a
c
e
+
(
d
ω
d
t
)
s
p
a
c
e
×
r
+
ω
×
(
d
r
d
t
)
s
p
a
c
e
=
(
d
v
R
d
t
)
s
p
a
c
e
+
α
×
r
+
ω
×
v
{\displaystyle {\begin{aligned}\mathbf {a} &\ {\stackrel {def}{=}}\ \left({\frac {\mathrm {d} \mathbf {v} }{\mathrm {d} t}}\right)_{\mathrm {space} }\\&=\left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {space} }+\left({\frac {\mathrm {d} ({\boldsymbol {\omega }}\times \mathbf {r} )}{\mathrm {d} t}}\right)_{\mathrm {space} }\\&=\left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {space} }+\left({\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\right)_{\mathrm {space} }\times \mathbf {r} +{\boldsymbol {\omega }}\times \left({\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\right)_{\mathrm {space} }\\&=\left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {space} }+{\boldsymbol {\alpha }}\times \mathbf {r} +{\boldsymbol {\omega }}\times \mathbf {v} \\\end{aligned}}}
其中,
α
=
d
e
f
(
d
ω
d
t
)
s
p
a
c
e
=
ω
˙
z
^
{\displaystyle {\boldsymbol {\alpha }}\ {\stackrel {def}{=}}\ \left({\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\right)_{\mathrm {space} }={\dot {\omega }}{\hat {\mathbf {z} }}}
應用算符方程式,
(
d
v
R
d
t
)
s
p
a
c
e
=
(
d
v
R
d
t
)
r
o
t
a
t
e
+
ω
×
v
R
=
a
R
+
ω
×
v
R
{\displaystyle \left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {rotate} }+{\boldsymbol {\omega }}\times \mathbf {v} _{R}=\mathbf {a} _{R}+{\boldsymbol {\omega }}\times \mathbf {v} _{R}}
其中,
a
R
=
d
e
f
(
d
v
R
d
t
)
r
o
t
a
t
e
=
x
¨
R
e
^
x
+
y
¨
R
e
^
y
{\displaystyle \mathbf {a} _{R}\ {\stackrel {def}{=}}\ \left({\frac {\mathrm {d} \mathbf {v} _{R}}{\mathrm {d} t}}\right)_{\mathrm {rotate} }={\ddot {x}}_{R}\ {\hat {\mathbf {e} }}_{x}+{\ddot {y}}_{R}\ {\hat {\mathbf {e} }}_{y}}
總合起來,質點P的加速度
a
=
x
¨
S
x
^
+
y
¨
S
y
^
{\displaystyle \mathbf {a} ={\ddot {x}}_{S}\ {\hat {\mathbf {x} }}+{\ddot {y}}_{S}\ {\hat {\mathbf {y} }}}
[ 3]
a
=
a
R
+
2
ω
×
v
R
+
α
×
r
+
ω
×
(
ω
×
r
)
{\displaystyle \mathbf {a} =\mathbf {a} _{R}+2{\boldsymbol {\omega }}\times \mathbf {v} _{R}+{\boldsymbol {\alpha }}\times \mathbf {r} +{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} )}
這方程式右手邊第一個項目是從旋轉參考系R觀測到的質點P的加速度項目,第二個是科里奧利力 項目,第三個是從空間參考系S觀測到的旋轉參考系R的角加速度項目,第四個是向心力 項目。
剛體的空間位形決定於其質心 位置與其取向 (最多有六個自由度 )。[ 4] 在物理學 裏,理想剛體 是一種有限尺寸,可以忽略形變 的固體 。不論是否感受到外力 ,在剛體內部,點 與點之間的距離 都不會改變。根據相對論 ,這種物體不可能實際存在,但物體通常可以假定為完美剛體,前提是必須滿足運動速度超小於光速 的條件。
剛體是由一群數量超多的質點組成。實際而言,不可能精確地追蹤其中每一個質點的運動。為了簡化運算,通常,整個剛體的空間位形可以簡易地以參數設定:
剛體的「位置」:挑選剛體內部一點G來代表整個剛體,通常會設定物體的質心 或形心 為這一點。從空間參考系S觀測,點G的位置就是整個剛體在空間的位置。位置可以應用向量的概念來表示:向量的起點為參考系S的原點,終點為點G。
剛體的取向 :描述剛體取向的方法有好幾種,包括方向餘弦 、歐拉角 、四元數 等等。這些方法設定一個附體參考系B的取向(相對於空間參考系S)。附體參考系是固定於剛體的參考系。相對於剛體,附體參考系的取向固定不變。由於剛體可能會呈加速度運動,所以附體參考系可能不是慣性參考系。空間參考系是某設定慣性參考系,例如,在觀測飛機的飛行運動時,附著於飛機場控制塔 的參考系可以設定為空間參考系,而附著於飛機的參考系則可設定為附體參考系。 歐拉旋轉定理 表明,在三維空間裏,假設約束剛體內部一點固定不動,則其任意位移等價於繞著某固定軸的一個旋轉,而這固定軸必包含這固定點。換句話說,設定附體參考系B的原點為這固定點,則附體參考系B不會因為這位移而涉及任何平移運動,這位移等價於繞著某固定軸的一個旋轉。[ 2]
剛體平移運動示意圖。 當剛體移動時,它的位置與取向都可能會隨著時間演進而改變。沙勒定理 歐拉旋轉定理 的一個推論 。根據沙勒定理,剛體的最廣義位移等價於一個平移加上一個旋轉。[ 2] 平移運動 與旋轉運動 。剛體的現在位置與現在取向可以視為是從某個初始位置與初始取向經過平移與旋轉而成。
如右圖所示,從時間
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
P
Q
¯
{\displaystyle {\overline {PQ}}}
挑選剛體內部一點G來代表整個剛體,設定附體參考系B的原點於點G(稱為「基點」),則從空間參考系S觀測,在剛體內部任意一點P的位置
r
P
{\displaystyle \mathbf {r} _{P}}
r
P
=
r
G
+
r
P
/
G
{\displaystyle \mathbf {r} _{P}=\mathbf {r} _{G}+\mathbf {r} _{P/G}}
其中,
r
G
{\displaystyle \mathbf {r} _{G}}
r
P
/
G
{\displaystyle \mathbf {r} _{P/G}}
從附體參考系B觀測,剛體內部每一點的位置都固定不變,但從空間參考系S觀測,剛體從時間
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
r
G
(
t
1
)
{\displaystyle \mathbf {r} _{G}(t_{1})}
r
G
(
t
2
)
{\displaystyle \mathbf {r} _{G}(t_{2})}
r
P
/
G
{\displaystyle \mathbf {r} _{P/G}}
t
1
{\displaystyle t_{1}}
t
2
{\displaystyle t_{2}}
從不同的參考系觀測剛體運動,可能會獲得不同的平移速度和不同的角速度。為了確保測量結果具有實際物理意義,必需先給定參考系。
剛體的平移速度是向量,是其位置向量的時間變化率,是附著於剛體的基點G的速度。對於純平移運動(沒有任何旋轉運動),剛體內部所有點的移動速度相同。假設涉及旋轉運動,則通常剛體內部任意兩點的瞬時速度不相等;只有當它們恰巧處於同一直軸,而這直軸平行於
角速度也是向量,描述剛體取向改變的角速率,和剛體旋轉時的瞬時轉軸的方向(歐拉旋轉定理 保證瞬時轉軸的存在)。在任意時間,剛體內部每一個質點的角速度相同。
假設一剛體呈純旋轉運動,旋轉的角速度為
ω
{\displaystyle {\boldsymbol {\omega }}}
F
{\displaystyle \mathbf {F} }
(
d
F
d
t
)
s
p
a
c
e
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }}
(
d
F
d
t
)
b
o
d
y
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {body} }}
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
F
d
t
)
s
p
a
c
e
=
(
d
F
d
t
)
b
o
d
y
+
ω
×
F
{\displaystyle \left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}\right)_{\mathrm {body} }+{\boldsymbol {\omega }}\times \mathbf {F} }
項目
ω
×
F
{\displaystyle {\boldsymbol {\omega }}\times \mathbf {F} }
F
{\displaystyle \mathbf {F} }
向量
F
(
t
)
{\displaystyle \mathbf {F} (t)}
(
d
d
t
)
s
p
a
c
e
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }}
(
d
d
t
)
b
o
d
y
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {body} }}
(
d
d
t
)
s
p
a
c
e
=
(
d
d
t
)
b
o
d
y
+
ω
×
{\displaystyle \left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {space} }=\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)_{\mathrm {body} }+{\boldsymbol {\omega }}\times }
這算符方程式可以作用於任意含時向量。
根據沙勒定理 ,剛體的最廣義位移等價於一個平移加上一個旋轉。[ 2]
r
P
{\displaystyle \mathbf {r} _{P}}
r
P
=
r
G
+
r
P
/
G
{\displaystyle \mathbf {r} _{P}=\mathbf {r} _{G}+\mathbf {r} _{P/G}}
其中,
r
G
{\displaystyle \mathbf {r} _{G}}
r
P
/
G
{\displaystyle \mathbf {r} _{P/G}}
點P的速度
v
P
=
(
d
r
P
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {v} _{P}=\left({\frac {\mathrm {d} \mathbf {r} _{P}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
v
P
=
v
G
+
v
P
/
G
{\displaystyle \mathbf {v} _{P}=\mathbf {v} _{G}+\mathbf {v} _{P/G}}
其中,
v
G
=
(
d
r
G
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {v} _{G}=\left({\frac {\mathrm {d} \mathbf {r} _{G}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
v
P
/
G
=
(
d
r
P
/
G
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {v} _{P/G}=\left({\frac {\mathrm {d} \mathbf {r} _{P/G}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
應用前段推導出的適用於任意含時向量的算符方程式,可以計算出
v
P
/
G
{\displaystyle \mathbf {v} _{P/G}}
(
d
r
P
/
G
d
t
)
b
o
d
y
{\displaystyle \left({\frac {\mathrm {d} \mathbf {r} _{P/G}}{\mathrm {d} t}}\right)_{\mathrm {body} }}
v
P
/
G
=
(
d
r
P
/
G
d
t
)
b
o
d
y
+
ω
×
r
P
/
G
=
ω
×
r
P
/
G
{\displaystyle \mathbf {v} _{P/G}=\left({\frac {\mathrm {d} \mathbf {r} _{P/G}}{\mathrm {d} t}}\right)_{\mathrm {body} }+{\boldsymbol {\omega }}\times \mathbf {r} _{P/G}={\boldsymbol {\omega }}\times \mathbf {r} _{P/G}}
其中,
ω
{\displaystyle {\boldsymbol {\omega }}}
所以,點P的速度為
v
P
=
v
G
+
ω
×
r
P
/
G
{\displaystyle \mathbf {v} _{P}=\mathbf {v} _{G}+{\boldsymbol {\omega }}\times \mathbf {r} _{P/G}}
點P的加速度
a
P
=
(
d
v
P
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {a} _{P}=\left({\frac {\mathrm {d} \mathbf {v} _{P}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
a
P
=
a
G
+
a
P
/
G
{\displaystyle \mathbf {a} _{P}=\mathbf {a} _{G}+\mathbf {a} _{P/G}}
其中,
a
G
=
(
d
v
G
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {a} _{G}=\left({\frac {\mathrm {d} \mathbf {v} _{G}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
a
P
/
G
=
(
d
v
P
/
G
d
t
)
s
p
a
c
e
{\displaystyle \mathbf {a} _{P/G}=\left({\frac {\mathrm {d} \mathbf {v} _{P/G}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
再應用前段推導出的算符方程式,可以計算出
a
P
/
G
=
(
d
ω
d
t
)
s
p
a
c
e
×
r
P
/
G
+
ω
×
v
P
/
G
=
α
×
r
P
/
G
+
ω
×
(
ω
×
r
P
/
G
)
{\displaystyle \mathbf {a} _{P/G}=\left({\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\right)_{\mathrm {space} }\times \mathbf {r} _{P/G}+{\boldsymbol {\omega }}\times \mathbf {v} _{P/G}={\boldsymbol {\alpha }}\times \mathbf {r} _{P/G}+{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} _{P/G})}
其中,
α
=
(
d
ω
d
t
)
s
p
a
c
e
{\displaystyle {\boldsymbol {\alpha }}=\left({\frac {\mathrm {d} {\boldsymbol {\omega }}}{\mathrm {d} t}}\right)_{\mathrm {space} }}
「運動約束」指的是一個動態系統的運動必須符合的約束 。以下列出一些例子:
假若,一個圓柱形物體質心 的速度
v
c
m
{\displaystyle \mathbf {v} _{cm}}
v
c
m
=
ω
×
r
c
m
/
O
{\displaystyle \mathbf {v} _{cm}={\boldsymbol {\omega }}\times \mathbf {r} _{cm/O}}
其中,
ω
{\displaystyle {\boldsymbol {\omega }}}
r
c
m
/
O
{\displaystyle \mathbf {r} _{cm/O}}
對於物體在滾動時不傾斜或不轉彎的案例,這約束條件約化為
v
=
r
c
m
/
O
ω
{\displaystyle v=r_{cm/O}\omega }
簡單擺的繩子長度保持不變。 當感受到張力 的作用時,「無伸縮性繩子」不會因為張力的大小而改變繩子的長度。對於涉及無伸縮性繩子的物理問題,約束條件是繩子長度保持不變[ 5]
單擺 :將一根無伸縮性繩子的一端固定,另外一端繫住一個錘。這就形成了一個簡單擺。在基礎動力學裏,簡單擺問題研究錘的擺動運動跟繩子長度、錘重量之間的關係。溜溜球 :在兩片圓盤之間連結的捲軸,繫著一根無伸縮性繩子。這就是古今中外、廣為流行的溜溜球玩具。懸鏈線 :將無伸縮性繩子的兩端分別固定於兩點,由於均勻重力 作用於繩子的每一部份而形成的曲線形狀稱為懸鏈線[ 6] Moon, Francis C. The Machines of Leonardo Da Vinci and Franz Reuleaux, Kinematics of Machines from the Renaissance to the 20th Century. Springer. 2007. ISBN 9781402055980






































![{\displaystyle {\begin{aligned}\mathbf {r} (t)&=\mathbf {r} _{0}+\int _{t_{0}}^{t}\mathbf {v} (t)\ \mathrm {d} t\\&=\mathbf {r} _{0}+\mathbf {v} _{0}t+\int _{t_{0}}^{t}\left[\int _{t_{0}}^{t}\mathbf {a} (t)\mathrm {d} t\right]\ \mathrm {d} t\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2872d50142876f276ca36fd99ef6d879bdec9ff9)




















































































































































