Lucid語言
| 編程範型 | 資料流程 |
|---|---|
| 設計者 | Edward A. Ashcroft William W. Wadge |
| 面市時間 | 1976年 |
| 主要實作產品 | |
| pLucid | |
| 衍生副語言 | |
| GIPSY, Granular Lucid | |
| 啟發語言 | |
| ISWIM | |
| 影響語言 | |
| SISAL, Pure Data, Lustre | |
Lucid是資料流程編程語言,設計用來實驗非馮·諾伊曼編程模型。它是William W. Wadge和Edward A. Ashcroft在1976年設計的[1],並描述於1985年的書籍《Lucid, the Dataflow Programming Language》[2]。
pLucid是Lucid的首個直譯器。
模型
[編輯]Lucid使用針對資料計算的需求驅動模型。每個語句都可以理解為一個方程,它定義了一個網路,即處理器和它們之間的資料經此流動的通訊線路。每個變數都是值的一個無限流(stream),而每個函式都是一個過濾器或變換器。Lucid最大的創新之處,是能夠進行流合成(composition)的迭代,這是通過「當前」值和算子fby(讀作followed by)來類比表述的。
Lucid基於了一種「歷史」(history)的代數,「歷史」是資料項的無限序列。在操作上,「歷史」可以被認為是一個變數的變更著的值的記錄,對「歷史」的運算操作比如first和next可以隨其名字所提示的那樣理解。Lucid最初被構想為一個規矩的、數學上純粹的單賦值語言,如此其驗證將會被簡化[3]。但是,資料流程釋義在Lucid的演變方向上有著重要的影響[4]。
細節
[編輯]Lucid從ISWIM繼承了where子句作為自己的塊結構,從POP-2繼承了資料類型。在Lucid中,每個表達式中的變數,都要先在表達式自身的where子句中尋找對應的變數定義,包含仍未約束的變數的表達式,在繼續進行(proceed)之前,要等待直到這個變數已經被約束,即等待從輸入中取得變數的值。一個表達式如x + y,在返回這個表達式的輸出之前,將等待直到x和y二者都成為約束的。這樣有一個重要結果,避免了更新有關值的顯式的邏輯,導致了相較於主流語言的先聲明再參照方式有大量的代碼簡約。
在Lucid中每個變數都是值的流(stream)。算子fby(followed by的助憶碼),定義了在前一個表達式之後會出現什麼。表達式n = 1 fby n + 1使用fby定義了一個流n,在這個實例中,這個流產生序列[1,2,3,...]。在流中的值,可以通過如下這些算子來定址取用,假定x是用到的變數:
first x- 取回在流x中的第一個值。每次求值這個表達式都得到同樣這個值。x- 取回在流x中當前值。next x- 取回在流x中當前值的下一個值。x asa p- 如果p提供了一個"true"值,則立刻(as soon as)提供x,否則在下一個x和下一個p上繼續進行此運算操作。每次求值這個表達式都得到同樣這個值。可以想像為它根據控制流p,從流x選取出第一個已經符合條件的值。x whenever p- 如果p提供了一個"true"值,則提供x;接著在下一個x和下一個p上繼續進行此運算操作。可以想像為它根據控制流p,從流x過濾出符合條件的所有值。它可以寫為助記碼wvr。x upon p- 提供x,如果p提供了一個"true"值,則在下一個x和下一個p上繼續進行此運算操作,否則在這個x和下一個p上繼續進行此運算操作。可以想像為它根據控制流p,在符合條件時放行流x的下一個值,在不符合條件時以重複當前值的方式滯留流x。x attime i- 將流i中的值作為流p中值的位次索引,依次從i取得索引選擇流x中指定位次的值。可以想像為它根據索引流i,對流x進行了選取和重組。X is current x- 將流x的當前值儲存在X變數中。每次求值X時都得到同樣的這個值。典型用於巢狀的內層迭代,它不能直接使用x而導致這個流的當前值順序前進的情況下,比如後面例子中的指數函式程式等。
計算是通過定義作用在資料的時變流上的過濾器或變換函式來完成的。涉及多個流的函式和運算操作採用逐點(pointwise)釋義比如:f(x,y) = [f(x0,y0),f(x1,y1),f(x2,y2),...],在後面例子中進行二個流的合併和串接時,因而在條件表達式if p then x else y fi中需要通過upon對要操作的流進行預處理。
資料結束(end of data)對象用預定義特殊識別碼eod表示,iseod eod將返回"true",此外所有的對eod的運算操作都產生eod。錯誤對象用預定義特殊識別碼error表示。index是預定義變數,它是以0開始的自然數序列。此外預定義變數還有true = "true"、false = "false"等。
例子
[編輯]total
where
total = 0 fby total + x
end
running_avg
where
sum = first(input) fby sum + next(input);
n = 1 fby n + 1;
running_avg = sum / n;
end
fac
where
n = 0 fby (n + 1);
fac = 1 fby (fac * (n + 1));
end
fib
where
fib = 0 fby (1 fby fib + next fib);
end
指數函式
[編輯]expsum asa next i eq 10
where
X is current x;
i = next index;
term = 1 fby (term / i) * X;
expsum = 0 fby expsum + term;
end
均方根
[編輯]sqroot(avg(square(a)))
where
square(x) = x*x;
avg(y) = mean
where
n = 1 fby n+1;
mean = first y fby mean + d;
d = (next y - mean)/(n+1);
end;
sqroot(z) = approx asa err < 0.0001
where
Z is current z;
approx = Z/2 fby (approx + Z/approx)/2;
err = abs(square(approx)-Z);
end;
end
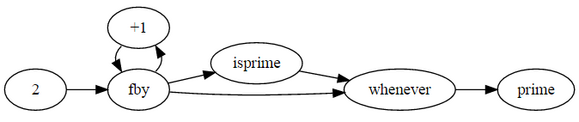
prime
where
prime = 2 fby (n whenever isprime(n));
n = 3 fby n+2;
isprime(n) = not(divs) asa divs or prime*prime > N
where
N is current n;
divs = N mod prime eq 0;
end;
end
漢明數
[編輯]計算升序的正規數的演算法經由戴克斯特拉得以流行,有關問題叫做「漢明問題」。Dijkstra計算這些數的想法如下:
- 漢明數的序列開始於數
1。 - 要加入序列中的數有下述形式:
2h,3h,5h,這裡的h是序列已有的任意的漢明數。 - 因此,可以生成最初只有一個
1的序列H,並接著合併序列2H,3H,5H,並以此類推。
hamming
where
h = 1 fby merge(merge(2 * h, 3 * h), 5 * h);
merge(x,y) = if xx <= yy then xx else yy fi
where
xx = x upon xx <= yy;
yy = y upon yy <= xx;
end;
end
注意這個程式中合併函式中的upon條件能夠起到二個流中可能存在的相同值在結果中只出現一個的效果。
資料流程圖
[編輯]快速排序
[編輯]下面程式實現了霍爾的快速排序演算法,將序列劃分為小於基準值(pivot)的元素和不小於它的元素的兩個子序列,然後遞迴的排序這兩個子序列,再將結果的兩個排好序的子序列串接起來。
qsort(a) = if iseod(first a) then a else follow(qsort(b0), qsort(b1)) fi
where
p = a < first a;
b0 = a whenever p;
b1 = a whenever not p;
follow(x,y) = if xdone then y upon xdone else x fi
where
xdone = iseod x
end
end
資料流程圖
[編輯]+--------> whenever -----> qsort ---------+ | ^ | | | | | not | | ^ | |---> first | | | | | | | V | | |---> less ---+ | | | | | V V ---+--------> whenever -----> qsort -----> follow -----> if-then-else -----> | ^ ^ | | | +--------> next ----> first ------> iseod --------------+ | | | +------------------------------------------------------------+
參照
[編輯]- ^ Edward A. Ashcroft, William W. Wadge. Lucid—A Formal System for Writing and Proving Programs (頁面存檔備份,存於網際網路檔案館). September 1976. SIAM Journal on Computing 5(3):336-354.DOI: 10.1137/0205029.
Edward A. Ashcroft, William W. Wadge. Lucid: Scope structures and defined functions (頁面存檔備份,存於網際網路檔案館). November 1976. TechnicalReport CS–76–22, Department of Computer Science, University of Waterloo. Published in 1978. - ^ Wadge, William W.; Ashcroft, Edward A. Lucid, the Dataflow Programming Language (PDF). Academic Press. 1985 [28 April 2020]. ISBN 0-12-729650-6. (原始內容存檔 (PDF)於2020-03-27).
- ^ Edward A. Ashcroft, William W. Wadge. LUCID, A Nonprocedural Language with Iteration[失效連結]. July 1977. in Communications of the ACM 20(7):519-526.
- ^ Online Historical Encyclopaedia of Programming Languages. [2020-05-02]. (原始內容存檔於2020-12-04).