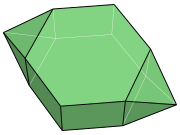
十四面體
| 部分的十四面體 | |
|---|---|
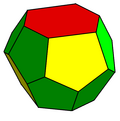 韋爾—費倫結構十四面體 |
 截半立方體 |
 十二角柱 |
 雙七角錐 |
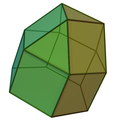 正三角帳塔柱 |
 恰薩爾十四面體 |
在幾何學中,十四面體是指由十四個面組成的多面體,而每個面都是正多邊形的十四面體有時稱為半正十四面體。
半正十四面體並不唯一,不像半正五面體、半正七面體只有一個,半正十四面體有四個,分別是截半立方體、截角立方體、截角八面體和正十二角柱。除了半正十四面體之外,十四面體可以是十三角錐、雙七角錐、七方偏方面體、正三角帳塔柱、同相雙三角帳塔、三側錐三角柱、截對角六方偏方面體、側帳塔截角四面體、恰薩爾十四面體等多面體[1]。在凸十四面體中,有1,496,225,352種不同拓樸結構的十四面體具有至少9個頂點[2]。
常見的十四面體
[编辑]十二角柱
[编辑]
十二角柱是一種底面為十二邊形的柱體,是十四面體的一種,其由14個面、36條邊和24個頂點組成。正十二角柱代表每個面都是正多邊形的十二角柱,其每個頂點都是2個正方形和1個十二邊形的公共頂點,頂點圖以表示,在施萊夫利符號中可以利用{12}×{} 或 t{2, 12}來表示;在考克斯特—迪肯符号中可以利用![]()
![]()
![]()
![]()
![]()
![]() 來表示;在威佐夫符號中可以利用2 12 | 2來表示;在康威多面體表示法中可以利用P12來表示。若一個正十二角柱底邊的邊長為、高為,則其體積和表面積為[3]:
來表示;在威佐夫符號中可以利用2 12 | 2來表示;在康威多面體表示法中可以利用P12來表示。若一個正十二角柱底邊的邊長為、高為,則其體積和表面積為[3]:
十三角錐
[编辑]十三角錐是一種底面為十三邊形的錐體,其具有14個面、26條邊和14個頂點,其對偶多面體是自己本身。正十三角錐是一種底面為正十三邊形的十三角錐。[4]。正十三角錐是一種底面為正十三邊形的十三角錐。若一個正十三角錐底邊的邊長為、高為,則其體積和表面積為[4]:
雙七角錐
[编辑]雙七角錐是指以七邊形做為基底的雙錐體,可以視為兩個七角錐以底面對底面組合成的多面體或一個七邊形(不含內部)的每一個頂點向它所在的平面外一點與該點由平面鏡射所產生的另外一個點依次連直線段而構成。所有雙七角錐都有14個面,21個邊和9個頂點[5]。
七方偏方面體
[编辑]在幾何學中,七方偏方面體(英語:Heptagonal Trapezohedron)是一個由14個全等的鳶形組成的多面體,為七角反角柱的對偶。所有七方偏方面體都有14個面、28條邊和16個頂點[6]。
四角罩帳
[编辑]
四角罩帳是指以四邊形為底的罩帳,是一種十四面體,由1個四邊形頂面、1個八邊形底面、4個五邊形側面和8個三角形側面組成,共有14個面、28條邊和16個頂點,其中四邊形與八邊形互相平行,三角形與五邊形交錯地圍繞軸分佈在周圍。
以正方形為底的四角罩帳稱為正四角罩帳,其僅有頂面和底面為正多邊形,分別為頂面的正方形和底面的正八邊形,側面可能可以存在正三角形或存在正五邊形,但有正三角形面時,五邊形最多僅能是等邊不等角的非正五邊形;有正五邊形面時,三角形會出現等腰三角形,故不屬於詹森多面體。唯一屬於詹森多面體的罩帳僅有正五角罩帳[7]。
正四角罩帳的對稱群為C4v群,階數為8階。
二側錐六角柱
[编辑]二側錐六角柱是指在六角柱的兩個四邊形側面上各疊上一個四角錐所構成的幾何體。
二側錐六角柱可以分成三種,一種是疊上的兩個四角錐位於六角柱兩相對的側面上,稱為對二側錐六角柱;一種是疊上的兩個四角錐中間相隔一個側面,稱為間二側錐六角柱;另一種是疊上一個四角錐位於六角柱上兩相鄰的四邊形側面上,稱為鄰二側錐六角柱。其中,間二側錐六角柱和對二側錐六角柱是一種詹森多面體。[8][9]
-
鄰二側錐六角柱
-
間二側錐六角柱
-
對二側錐六角柱
半正十四面體
[编辑]半正多面體並非只包含阿基米德立體[10][11],它包含了所有由正多邊形組成且具有嚴格對稱的多面體,包含了正稜柱和正反稜柱。其中14個面的半多面體包括了3個阿基米德立體和1個正稜柱,分別為截半立方體、截角立方體、截角八面體和十二角柱。[12]
| 名稱 (頂點佈局) |
旋轉透視圖 | 立體圖 | 展開圖 | 面 | 邊 | 頂點 | 所屬點群 | |
|---|---|---|---|---|---|---|---|---|
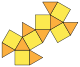
| 截半立方體 (截半八面體) (3.4.3.4) |

|

|
|
14 | 正三角形×8 正方形×6 |
24 | 12 | Oh群 |
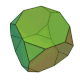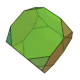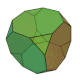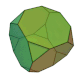
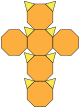
| 截角立方體 (3.8.8) |
|

|
|
14 | 三角形×8 八邊形×6 |
36 | 24 | Oh群 |
| 截角八面體 (4.6.6) |

|

|

|
14 | 正方形×6 六邊形×8 |
36 | 24 | Oh群 |
| 十二角柱 (4.4.12) |

|
14 | 正方形×10 十二邊形×2 |
36 | 24 | D12h | ||
詹森多面體
[编辑]共有8個詹森多面體具有14個面,分別為正三角帳塔柱、同相雙三角台塔、三側錐三角柱、二側錐六角柱(兩種)、側台塔截角四面體、球狀屋頂和雙新月雙罩帳[13]。
| 名稱 | 種類 | 圖像 | 編號 | 頂點 | 邊 | 面 | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|
| 正三角帳塔柱 | 帳塔柱 | 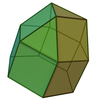
|
J18[14] | 15 | 27 | 14 | 4個正三角形 9個正方形 1個六邊形 |
C3v | 
|
| 同相雙三角台塔 | 同相雙帳塔 | 
|
J27[15] | 12 | 24 | 14 | 8個正三角形 6個正方形 |
D3h | 
|
| 三側錐三角柱 | 側錐柱 | 
|
J51[16] | 9 | 21 | 14 | 14個正三角形 |
D3h | 
|
| 對二側錐六角柱 | 側錐柱 | 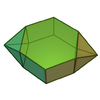
|
J55[17] | 14 | 26 | 14 | 8個正三角形 4個正方形 2個六邊形 |
D2h | 
|
| 間二側錐六角柱 | 側錐柱 | 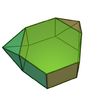
|
J56[18] | 14 | 26 | 14 | 8個正三角形 4個正方形 2個六邊形 |
C2v | 
|
| 側台塔截角四面體 | 側帳塔阿基米德立體 | 
|
J65[19] | 15 | 27 | 14 | 8個正三角形 3個正方形 3個六邊形 |
C3v | 
|
| 球狀屋頂 | 
|
J86[20] | 10 | 22 | 14 | 12個正三角形 2個正方形 |
C2v | 
| |
| 雙新月雙罩帳 | 
|
J91[21] | 14 | 26 | 14 | 8個正三角形 2個正方形 4個正五邊形 |
D2h | 
|
十四面體列表
[编辑]| 名稱 | 種類 | 圖像 | 符號 | 頂點 | 邊 | 面 | χ | 面的種類 | 對稱性 | 展開圖 |
|---|---|---|---|---|---|---|---|---|---|---|
| 十二角柱 | 稜柱體 | 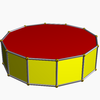
|
t{2,12} {12}x{} |
24 | 36 | 14 | 2 | 2個十二邊形 12個矩形 |
D12h, [12,2], (*12 2 2) | |
| 十三角錐 | 稜錐體 | ( )∨{13} | 14 | 26 | 14 | 2 | 1個十三邊形 13個三角形 |
C13v, [13], (*13 13) | ||
| 六角反棱柱 | 反棱柱 | 
|
s{2,12} sr{2,6} |
12 | 24 | 14 | 2 | 2個六邊形 12個三角形 |
D6d, [2+,12], (2*6), 24階 | |
| 六角帳塔 | 帳塔 | {6}||t{6} | 18 | 30 | 14 | 2 | 6個三角形 6個正方形 1個六邊形 1個十二邊形 |
C6v, [1,6], (*66), 12階 | ||
| 雙七角錐 | 雙錐體 | 
|
{ }+{7} | 9 | 21 | 14 | 2 | 14個三角形 | D7h, [7,2], (*722), 28階 | |
| 七方偏方面體 | 偏方面體 | 
|
{ }⨁{7}[22] | 16 | 28 | 14 | 2 | 14個鷂形 | D7d, [2+,7], (2*7) | |
| 四角罩帳 | 罩帳 | 
|
16 | 28 | 14 | 2 | 1個四邊形頂面 1個八邊形底面 4個五邊形側面 8個三角形側面 |
C4v, [4], (*44), 8階 | ||
| 截對角六方偏方面體 | 截對角偏方面體 | 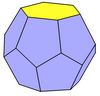
|
24 | 36 | 14 | 2 | 2個五邊形側面 2個六邊形底面 |
D6d, [12,2+], 2*6, 24階 | ||
| 鄰二側錐六角柱 | 側錐柱 | 
|
14 | 26 | 14 | 2 | 8個正三角形 4個正方形 2個六邊形 |
|||
| 韋爾—費倫結構十四面體 | 空間填充立體對 | 
|
24 | 36 | 14 | 2 | 4+8個五邊形 2個六邊形 |
|||
| 恰薩爾十四面體 | 环形多面体 | 
|
7 | 21 | 14 | 0 | 2個等邊三角形 2個等腰三角形 10個鈍角三角形 |
C1, [ ]+, (11) |
參考文獻
[编辑]- ^ Weisstein, Eric W. (编). Tetradecahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Counting polyhedra (页面存档备份,存于互联网档案馆) numericana.com [2016-1-10]
- ^ Wolfram, Stephen. "Dodecagon prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ 4.0 4.1 Wolfram, Stephen. "Tridecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ Dipyramids & Trapezohedra: Heptagonal Dipyramid. dmccooey.com. [2019-09-29]. (原始内容存档于2019-09-29).
- ^ Dipyramids & Trapezohedra: Heptagonal Trapezohedron. dmccooey.com. [2019-09-29]. (原始内容存档于2019-09-29).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- ^ Weisstein, Eric W. (编). Metabiaugmented hexagonal prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Parabiaugmented hexagonal prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 《圖解數學辭典》天下遠見出版 ISBN 986-417-614-5
- ^ Illustrated Dictionary of Maths 2003 Usborne Publishing Ltd.
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. Uniform polyhedra (PDF). Philosophical Transactions of the Royal Society A. 1954, 246 (916): 401–450 [2019-09-29]. ISSN 0080-4614. JSTOR 91532. MR 0062446. doi:10.1098/rsta.1954.0003. (原始内容存档 (PDF)于2017-12-01).
- ^ Johnson, Norman W., Convex polyhedra with regular faces, Canadian Journal of Mathematics, 1966, 18: 169–200, MR 0185507, Zbl 0132.14603, doi:10.4153/cjm-1966-021-8.
- ^ Weisstein, Eric W. (编). Elongated Triangular Cupola. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Triangular Orthobicupola. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Triaugmented Triangular Prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Parabiaugmented Hexagonal Prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Metabiaugmented Hexagonal Prism. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Augmented Truncated Tetrahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Sphenocorona. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Bilunabirotunda. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Johnson, N.W. Chapter 11: Finite symmetry groups. Geometries and Transformations. 2018. 11.3 Pyramids, Prisms, and Antiprisms, Figure 11.3c. ISBN 978-1-107-10340-5.