功率分配器与定向耦合器


功率分配器与定向耦合器是主要用于无线电或微波领域的被动元件。它们将传输线中的电磁功率耦合到端口,使得信号能够用在另一个电路中。定向耦合器的一个基本特征是它们只将电磁功率耦合到固定的方向。在两个端口平均分配功率的定向耦合器又称为混合耦合器。
定向耦合器最常由两个耦合的传输线构成,这两个传输线足够靠近,使得其中一个的能量能耦合到另一个。这种技术在微波频率上是有利的,其中传输线设计通常用于实现许多电路元件。然而,集中式组件也可以在较低频率下使用,例如电话中遇到的音频频率。同样在微波频率,特别是较高频带,可以使用波导设计。这些波导耦合器中的许多对应于导电传输线设计中的一个,但是也存在波导特有的类型。
定向耦合器和功率分配器有许多应用。这些包括提供用于测量或监视的信号样本、反馈、组合来自天线的馈送、天线波束成形,为诸如有线电视的有线分布式系统提供分接头,以及在电话线上分离发送和接收信号。
符号
[编辑]

最常用于定向耦合器的符号如图1所示。符号可以在其上标记以dB为单位的耦合因子。定向耦合器有四个端口。端口1是应用电源的输入端口。端口3是耦合端口,其中出现应用于端口1的一部分功率。端口2是输出端口1的电源输出的端口,少于端口3的输出端口。定向耦合器通常是对称的,因此也存在端口4,即隔离端口。施加到端口2的一部分功率将耦合到端口4.但是,该设备通常不用于此模式,端口4通常以匹配负载(通常为50欧姆)终止。 该终止可以在设备内部,并且用户不能访问端口4。实际上,这导致3端口设备,因此图中的定向耦合器的第二符号的效用[1]。
“端口a处的参数P由于端口b处的输入”。
功率分配器的符号如图2所示。功率分配器和定向耦合器都属于同一类器件。定向耦合器通常是较少耦合的4端口器件,只有一小部分输入功率出现在耦合端口上。功率分配器则相反,多数功率能到达输出端口,常被视为三端口器件。[2]
参数
[编辑]当其他端口都匹配负载时,所有定向耦合器所需的共同特性是较大的带宽、高定向性和所有端口的良好阻抗匹配[3]。
耦合系数
[编辑]耦合系数的定义为:
其中P1是端口1的输入功率,P3是耦合端口3的输出功率。
耦合系数是定向耦合器的主要特性参数。它是负数的,对于无源器件不能超过0 dB,并且通常小于−3 dB ,因为输出功率不可能比输入功率多。在其他文献里,常会省略负号,甚至定义为正数[4] 。
耦合系数会随着频率而变化。虽然不同的设计可以减少方差,但理论上不能构建完美平坦的耦合器。定向耦合器是根据频带中心的耦合精度来规定的。[5]
损失参数
[编辑]
从端口1到端口2的插入损失(P1 – P2) 是:
插入损失:
部分损失是由于某些功率进入耦合端口而被称为耦合损失,由下式给出:
耦合损失:
理想定向耦合器的插入损耗完全由耦合损耗组成。理想定向耦合器的插入损耗完全由耦合损耗组成。然而,实际定向耦合器中,插入损耗包括耦合损失、电介质损失,导体损失和驻波比损失。根据频率范围,耦合损耗在 15 dB耦合之上变得不那么显著,其他损耗构成总损耗的大部分。耗散耦合器的理论插入损失(dB)与耦合(dB)的关系如图3和下表所示。[6]
| 耦合系数 | 插入损失 |
|---|---|
| dB | dB |
| 3 | 3.00 |
| 6 | 1.25 |
| 10 | 0.458 |
| 20 | 0.0436 |
| 30 | 0.00435 |
隔离度
[编辑]定向耦合器的隔离度可以定义为当其他两个端口由匹配负载时,输入端口和隔离端口之间的信号能差(以dB为单位)。隔离度定义如下式:
也可以在两个输出端口之间定义隔离。在这种情况下,其中一个输出端口用作输入; 另一个被认为是输出端口,而另外两个端口(输入和隔离)则匹配负载。因此定义如下:
输入端口和隔离端口之间的隔离可能与两个输出端口之间的隔离不同。 例如,端口1和4之间的隔离可以是 30 dB,而端口2和3之间的隔离可以是不同的值,例如 25 dB。 可以从耦合加上回波损耗估算隔离。 隔离度应尽可能高。 在实际的耦合器中,隔离端口永远不会完全隔离。 一些射频功率将始终存在。 波导定向耦合器将具有最佳隔离度。[6]
定向性
[编辑]定向性与隔离直接相关。 它被定义为:
其中: P3是耦合端口的输出功率,P4是隔离端口的功率输出。
定向性越高越好。定向性随频率改变而变化,并且在设计的频率点上特别高。定向性对频率特别敏感,因为它是两个波分量的差。波导定向耦合器将具有最佳定向性。定向性无法直接测量,需要通过增加隔离度和耦合系数测量来计算:[7]
如果使用正的耦合系数,则公式改为:
散射参数
[编辑]理想无限隔离与完全匹配且对称定向耦合器的散射参数由下式给出,
- 是传输系数。
- 是耦合系数。
通常与都是复数,并且随频率变化。矩阵主对角线上0代表阻抗匹配,任何端口的功率输入都不会反射回同一个端口。在反对角线上,0代表输入和隔离端口之间完美隔离。
对于无源无损定向耦合器,其矩阵为幺正矩阵:
因为进入输入端口的能量必须全部由其他两个端口之一离开。[8]
插入损失与相关;
耦合系数与相关;
主对角线上飞零代表有回波损失;反对角线上非零则代表隔离不完全。然而,部分作者定义了端口号3和4互换的端口号。这导致散射矩阵在反对角线上不再是全零。[9]
幅度平衡
[编辑]幅度平衡指的是3dB混合器的两个输出端口之间的功率差异(dB)。在理想的功率平分器中,其差值应为0dB。 然而,实际上,幅度平衡取决于频率并且偏离理想的0dB[7]。
相位平衡
[编辑]相位平衡定义为两个输出段口的相位差。理想情况,混合耦合器的两个输出端口之间的相位差应为0°,90°或180°。然而,与幅度平衡一样,相位差依输入频率而变化[7]。
传输线模型
[编辑]定向耦合器
[编辑]耦合传输线
[编辑]
定向耦合器的最常见形式是一对耦合传输线。它们可以通过多种技术实现,包括同轴和平面技术(微带线与带状线)。图4中的四分之一波长(λ/ 4)定向耦合器为带状线。耦合线上的功率以与主线上的功率呈反方向流动,因此端口布置与图1中所示的不同,但编号保持相同。因此,它有时被称为“后向耦合器”。[10]
端口1与端口2之间是“主线”;端口3与端口4之间是“耦合线”。由于定向耦合器是线性器件,因此图1中的符号是任意的。任何端口都可以是输入端(如图20所示),这将导致直接连接的端口是传输端口,相邻端口是耦合端口,对角端口是隔离端口。在一些定向耦合器上,主线设计用于高功率操作(大型连接器),而耦合端口可以使用小型连接器,例如SMA连接器。内部负载额定功率也可能限制耦合线路上的操作。[3]

耦合系数的精度取决于两条耦合线间距的尺寸公差。对于平面印刷技术,这取决于印刷过程的分辨率,决定了可以产生的最小轨道宽度,并且还限制两条线的间距。当需要非常紧密的耦合并且经常使用不同的设计 3dB的耦合器时,这成为一个问题。然而,可以在空气带状线中生产紧密耦合的线,这也允许通过印刷平面技术制造。在这种设计中,两条线印刷在电介质的“相对”侧面而不是并排。两条线在它们的宽度上的耦合远大于它们彼此边缘接合时的耦合。 [11]
λ/ 4耦合线设计适用于同轴和带状线实现,但在现在流行的微带格式中不能很好地工作,尽管设计确实存在。原因是微带不是均匀介质 - 传输带上方和下方有两种不同的介质。这导致除了导电电路中常见的TEM模式之外的横向模式。偶模和奇模的传播速度不同,导致信号色散。微带线的更好解决方案是比λ/ 4短得多的耦合线,如图5所示,但这具有耦合因子随频率显著上升的缺点。有时遇到的这种设计的变型使得耦合线具有比主线更高的特性阻抗,如图6所示。这种设计在将耦合器馈送到用于功率监测的检测器的情况下是有利的。对于给定的主线功率,较高阻抗线导致较高的射频电压,使得检测器二极管的工作更容易[12]。
制造商规定的频率范围是耦合线的频率范围。主线响应要宽得多:例如, 2-4 GHz指定的耦合器可能有一条可以在 1-5 GHz运行的主线。主线响应要宽得多:例如, 2-4 GHz指定的耦合器可能有一条可以在 1-5 GHz运行的主线。 与所有分布式元件电路一样,耦合响应是频率周期性的。 例如,λ/ 4耦合线耦合器将在nλ/ 4处具有响应,其中n是奇整数。[3]
单个λ/ 4耦合部分适用于小于八度的带宽。 为了获得更大的带宽,使用多个λ/ 4耦合部分。 这种耦合器的设计与分布式元件滤波器的设计大致相同。 耦合器的各部分被视为滤波器的部分,通过调整每个部分的耦合系数,可以使耦合端口具有任何经典滤波器响应,例如最大平坦(巴特沃斯滤波器), 等纹波(椭圆函数滤波器)或指定纹波(切比雪夫滤波器)响应。 纹波滤波器是通带中耦合端口输出的最大变化,通常用标称耦合因子作为正或负的dB值[13]。

可以看出,耦合线定向耦合器的纯实数,而在所有频率上都是纯虚数的。这导致S矩阵的简化以及耦合端口始终与输出端口处于正交相位相位(90°)的结果。一些应用程序利用这种相位差。 让,无损操作的理想情况简化为[14]:
分支线耦合器
[编辑]
分支线耦合器由两条物理耦合在一起的并行传输线组成,它们之间有两条或多条支路。分支线间隔λ/ 4并且以与耦合线耦合器的多个部分相同的方式表示多部分滤波器设计的部分,除了这里每个部分的耦合由分支线的阻抗控制。主线和耦合线是系统阻抗的。耦合器中的部分越多,分支线的阻抗比越高。高阻抗线具有窄轨道,并且由于制造限制,这通常将设计限制为平面格式的三个部分。类似的限制适用于比 10 dB宽松的耦合因子;低耦合也需要窄轨道。当需要松耦合时,耦合线是更好的选择,但分支线耦合器适用于紧耦合,可用于 3 dB混合。分支线耦合器通常不具有如耦合线那样宽的带宽。这种类型的耦合器适用于高功率、空气介电、实心棒形式,因为刚性结构易于机械支撑。[15]
蓝泽耦合器
[编辑]蓝泽耦合器的结构类似于交叉指形滤波器,并行的线路交错以实现耦合。它用于 3 dB到 6 dB范围内的强耦合[16]。
功率分配器
[编辑]
最早的传输线功率分配器是简单的T型接头。它们在输出端口之间的隔离非常差,从端口2反射出来的功率很多都会进入端口3。三端口网络不能同时达到“无损”、端口匹配负载、“互易”。然而,这四端口网络可以达到这些条件,可以设计四端口设备,使到达端口2的功率在端口1之间分配,端口4以匹配负载,端口3隔离。[17]
术语“混合耦合器”最初应用于3 dB耦合线定向耦合器,即其中两个输出均为输入功率的一半。 这同义词意味着正交 3dB耦合器,输出相位相差90°。 现在任何带有隔离端和相等功率分配的匹配4端口称为混合耦合器。 其他类型可以具有不同的相位关系。 如果为90°,则为90°混合,如果为180°,则为180°混合等。在本文中,没有限定条件的“混合耦合器”意味着耦合线混合。[18]
威尔金森功率分配器
[编辑]
威尔金森功率分配器由两个并联的非耦合λ/4传输线组成。输入并行馈送到两条线路,输出端接两圈的系统阻抗。该设计可以采用平面格式实现,但它在同轴电缆中具有更自然的实现:在平面中,两条线必须保持分开,这样它们不会耦合,而是必须在它们的输出端汇集在一起,这样它们就可以被端接而不是在同轴电缆中,线路可以依靠同轴外导体并排运行以进行筛选。
威尔金森功率分配器解决了简单T型接头的匹配问题:它在所有端口具有低电压驻波比,在输出端口之间具有高隔离度。每个端口的输入和输出阻抗设计为等于微波系统的特征阻抗。这是通过使系统阻抗的线阻抗 来实现的 - 对于50Ω系统,威尔金森线约为70 Ω。[19]
混合耦合器
[编辑]上面描述了耦合线定向耦合器。当耦合设计为 3dB时,它被称为混合耦合器。理想的对称混合耦合器的S矩阵减少到:
两个输出端口具有90°相位差(-“i”至-1),因此这是90°混合。[20]
混合环型耦合器
[编辑]
混合环型耦合器,也称为鼠标耦合器,是一个四端口 3dB定向耦合器,由一个3λ/ 2环形传输线组成,其中四条线的间隔为如图12所示。端口1处的电源输入在环上分开并双向传播。在端口2和3处,信号同相到达并且在端口4处增加,但是它是异相所以被消除。端口2和3彼此同相,因此这是0°混合的示例。图12示出了平面实现,但是该设计也可以在同轴或波导中实现。通过使环的每个λ/ 4部分交替地低和高阻抗,但是对于 3dB耦合器,可以产生具有与 3dB不同的耦合因子的耦合器。 环是的端口阻抗,对于50Ω设计,环大约为70Ω[21]。
混合环型耦合器的S参数矩阵为:
混合环的端口不对称;选择不同输入端口不一定产生相同的结果。从端口1或端口3输入,混合环是如所述的0°混合。但是,输入端口2或端口4会产生180°混合。[22]
这一事实导致混合环的另一个有用的应用:它可用于从两个输入信号产生和(Σ)和差(Δ)信号,如图12所示。对于端口2和3的输入,出现Σ信号在端口1处,Δ信号出现在端口4处[23]。
多输出分频器
[编辑]
典型的功率分配器如图13所示。理想情况下,输入功率将在输出端口之间平均分配。分频器由多个耦合器组成,与耦合器一样,可以反转并用作多工器。缺点是对于四通道多路复用器,输出仅由每个功率的1/4组成,并且效率相对较低。其原因在于,在每个组合器的一半输入功率到达端口4并在终端负载中耗散。如果两个输入是相干,则可以安排相位,使得在端口4处发生消除,然后所有功率将转到端口1。但是,多路复用器输入通常来自完全独立的源,因此不连贯。无损多路复用只能通过滤波器网络完成。[24]
波导类型
[编辑]波导定向耦合器
[编辑]波导分支线耦合器
[编辑]上述波导分支线耦合器也可以在波导中实现。[25]
倍兹孔方向耦合器
[编辑]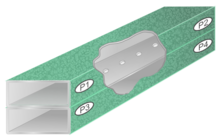
倍兹孔方向耦合器是最常见、最简单的波导定向耦合器之一。 它由两个平行的波导组成,一个堆叠在另一个的顶部,在它们之间有一个孔。一个导向装置的一些功率通过孔进入另一个导向装置。倍兹孔方向耦合器是后向耦合器的另一个例子。[26]
倍兹孔方向耦合器的概念可以通过提供多个孔来扩展。孔间隔λ/ 4。这种耦合器的设计与多段耦合传输线相似。使用多个孔可以通过将这些部分设计为巴特沃斯、契比雪夫或其他一些滤波器类来扩展带宽。选择孔尺寸以为过滤器的每个部分提供所需的耦合。设计标准是在所需频带上实现基本上平坦的耦合以及高方向性[27]。
瑞雷特短槽藕合器
[编辑]瑞雷特短槽藕合器是两个波导并排,侧壁是共同的,而不是像倍兹孔方向耦合器那样的长边。在侧壁上切出一个槽以允许耦合。这种设计经常用于产生 3dB耦合器。[28]
施温格反相耦合器
[编辑]施温格反相耦合器是另一种使用平行波导的设计,这次一侧的长边与另一侧的短侧壁相同。 在间隔λ/ 4的波导之间切割两个偏心槽。施温格是一个后向耦合器。与Bethe-hole耦合器相比,这种设计具有基本上平坦的方向性响应和与频率相关的强耦合的缺点,倍兹孔方向耦合器的耦合因子几乎没有变化。[29]
莫仑诺十字形波导耦合器
[编辑]莫仑诺十字形波导耦合器有两个波导,一个堆叠在另一个上面,像倍兹孔方向耦合器,但彼此成直角而不是平行。在波导之间的对角线上切割两个通常为十字形的偏心孔,距离分开。莫仑诺十字形波导耦合器适用于紧耦合应用。 这是倍兹孔方向耦合器和莫仑诺耦合器的特性之间的折衷,其耦合和方向性随频率而变化。[30]
波导功率分配器
[编辑]波导混合环
[编辑]上面讨论的波导混合环也可以在波导中实现。[31]
幻T形接头
[编辑]
首先通过简单的T形接头完成相干功率分配。 在微波频率下,波导三通有两种可能的形式:E与H平面。这两个结均等地分配功率,但由于结处的场结构不同,输出臂处的电场与H平面三通同相,并且对于E平面三通为180°异相。 这两个发球台的组合形成混合发球台被称为魔T。魔T是一个四端口组件,可以执行两个相干微波信号的矢量和(Σ)和差值(Δ)。[32]
集总元件
[编辑]混合变压器
[编辑]
标准的3dB混合变压器如图16所示。端口1的电源在端口2和3之间平均分配,但相互反相。因此,混合变压器是180°混合动力。中心抽头通常在内部端接,但可以将其作为端口4引出; 在这种情况下,混合可以用作和和混合。但是,端口4表示与其他端口不同的阻抗,如果需要在相同的系统阻抗下使用该端口,则需要额外的变压器进行阻抗转换。[33]
混合变压器通常用于电信中,用于2到4线转换。电话手机包括这样的转换器,用于将2线线路转换为来自耳机和吹嘴的4线。[34]
交叉连接变压器
[编辑]
对于较低的频率(小于 600 MHz),可以通过RF变压器实现紧凑的宽带实现。在图17中,示出了用于弱耦合的电路,并且可以沿着这些线理解:信号进入一个线对。一个变压器降低信号电压,另一个变压器降低电流。因此,阻抗匹配。相同的论证适用于通过耦合器的信号的每个其他方向。感应电压和电流的相对符号决定了输出信号的方向[35]。
耦合由下式给出:
其中n是次级匝数比。
对于 3 dB耦合,即在发送端口和耦合端口之间信号的相等分割,,并且隔离端口以两次终止 50Ω系统的特征阻抗 - 100Ω。基于该电路的 3dB功率分配器具有彼此180°相位的两个输出,与具有90°相位关系的λ/ 4耦合线相比。[36]
电阻性T形接头
[编辑]
简单电阻性T形电路可用作功率分配器,如图18所示。通过Y-Δ变换,该电路也可以实现为Δ电路。使用增量形式电阻器等于系统阻抗。这可能是有利的,因为系统阻抗值的精密电阻器总是可用于大多数系统标称阻抗。 三通电路具有简单,低成本和本质上宽带宽的优点。 它有两个主要缺点; 首先,电路将耗散功率,因为它是电阻性的:相等的分裂将导致 6 dB插入损耗而不是 3 dB。 第二个问题是 0 dB方向性导致输出端口之间的隔离非常差。[37]
对于不均等的功率分配,插入损耗不是问题:例如端口3处的 -40 dB在端口2处具有小于 0.2 dB的插入损耗。隔离可以是通过用T pad s替换输出电阻,以两个输出端口的插入损耗为代价进行了改进。 隔离改善大于增加的插入损耗。[38]
6dB电阻桥式混合电路
[编辑]
真正的混合分配器/耦合器理论上可以通过电阻桥电路实现无限隔离和方向性。与三通电路一样,电桥具有 6 dB插入损耗。它的缺点是不添加变压器就不能用于不平衡电路; 但是,如果插入损耗不是问题,它是600Ω平衡通信线路的理想选择。桥中代表端口的电阻器通常不是器件的一部分(端口4除外,它可能在内部永久端接),这些电阻由线路终端提供。因此,该装置基本上由两个电阻器(加上端口4终端)组成[39]。
应用
[编辑]监测
[编辑]定向耦合器的耦合输出可用于监视信号的频率和功率电平,而不会中断系统中的主要功率流(功率降低除外,见图3)[3]。
利用隔离
[编辑]
如果隔离度很高,定向耦合器有利于组合信号以将单线馈送到接收器以进行双音接收机测试。在图20中,一个信号进入端口P3,一个进入端口P2,而两个出口P1。从端口P3到端口P1的信号将经历 10 dB的丢失,并且来自端口P2的信号到端口P1将失去 0.5 dB。隔离端口上的内部负载将消除端口P3和端口P2的信号损耗。如果忽略图20中的隔离器,则隔离测量(端口P2到端口P3)确定来自信号产生器 的功率量F2将被注入信号发生器 F1。随着注入水平的增加,它可能导致信号发生器F1的调制,甚至注入锁相。由于定向耦合器的对称性,反向注入将发生与F1的信号发生器F2相同的可能调制问题。因此,在图20中使用隔离器以有效地增加定向耦合器的隔离(或方向性)。因此,注入损耗将是定向耦合器的隔离加上隔离器的反向隔离[40]。
混合电路
[编辑]混合电路的应用包括单脉冲比较器、频率混频器、功率合成器、分频器、调制器和相控阵雷达天线系统。两个同相设备(例如威尔金森分频器)和正交(90°)混合耦合器可用于相干功率分配器应用。[41]
在家中使用便宜版本的功率分配器将有线电视或无线电视信号分配给多个电视机和其他设备。具有两个以上输出端口的多端口分离器通常由多个级联耦合器内部组成。域内宽带互联网服务可由有线电视公司提供(有线互联网)。域内用户的互联网电缆调制解调器连接到分离器的一个端口[42]。
功率合成器
[编辑]由于混合电路是双向的,因此它们可以用于相干地组合功率以及分离功率。在图21中,示出了分离以馈送多个低功率放大器的信号的示例,然后重新组合以馈送具有高功率的单个天线[2]。


每个功率组合器的输入的相位被布置成使得两个输入彼此异相90°。由于混合组合器的耦合端口与发送端口成90°异相,这导致功率在组合器的输出处相加并在隔离端口处抵消:图22中的代表性示例在图22中示出。注意,每个组合器/分配器的两个端口都有一个额外的固定90°相移,为简单起见,图中未示出[20] 。
对两个输入端口施加同相功率将无法获得所需的结果:两个输入端的正交总和将出现在两个输出端口:这是每个输出端口总功率的一半。这种方法允许在电路中使用许多更便宜和更低功率的放大器而不是单个高功率行波管。另一种方法是让每个固态放大器(SSA)馈送天线并使功率在空间中组合或用于馈送连接到天线的镜头[43]。
相位差
[编辑]
90°混合耦合器的相位特性可用于微波电路中的巨大优势。 例如,在平衡微波放大器中,两个输入级通过混合耦合器馈电。 场效应晶体管器件通常具有非常差的匹配并且反射大部分入射能量。然而,由于器件基本相同,因此来自每个器件的反射系数相等。来自FET的反射电压在隔离端口处同相,并且在输入端口处为180°不同。因此,来自FET的所有反射功率都会进入隔离端口的负载,并且没有电源进入输入端口。这导致良好的输入匹配(低驻波比)。[7]
如果相位匹配线用于180°混合耦合器的天线输入,如图23所示,则零点将直接出现在天线之间。要在该位置接收信号,必须改变混合类型或线路长度。 要拒绝来自给定方向的信号,或为单脉冲雷达创建差异模式,这是一种很好的方法[44]。
通过将相位延迟到天线阵列的下部元件,可以使用相位差耦合器在VHFFM 无线电台中创建波束倾斜。更一般地,相位差耦合器与固定相位延迟和天线阵列一起用于诸如巴特勒矩阵的波束形成网络中,以在任何规定方向上创建无线电波束[45]。
参考文献
[编辑]- ^ Ishii, p.200
Naval Air Warfare Center, p.6-4.1 - ^ 2.0 2.1 Räisänen and Lehto, p.116
- ^ 3.0 3.1 3.2 3.3 Naval Air Warfare Center, p.6.4.1
- ^ For instance; Morgan, p.149
- ^ Naval Air Warfare Center, p.6.4.1
Vizmuller, p.101 - ^ 6.0 6.1 Naval Air Warfare Center, p.6.4.2
- ^ 7.0 7.1 7.2 7.3 Naval Air Warfare Center, p.6.4.3
- ^ Dyer, p.479
Ishii, p.216
Räisänen and Lehto, pp.120–122 - ^ For instance, Räisänen and Lehto, pp.120–122
- ^ Morgan, p.149
Matthaei et al., pp.775–777
Vizmuller, p.101 - ^ Naval Air Warfare Center, p.6.4.1
Matthaei et al., pp.585–588, 776–778 - ^ Räisänen and Lehto, pp.124–126
Vizmuller, pp.102–103 - ^ Naval Air Warfare Center, p.6.4.1
Matthaei et al., pp.775–777 - ^ Ishii, p.216
Räisänen and Lehto, p.120-122 - ^ Ishii, pp.223–226
Matthaei et al., pp.809–811
Räisänen and Lehto, p.127 - ^ Räisänen and Lehto, p.126
- ^ Räisänen and Lehto, pp.117–118
- ^ Naval Air Warfare Center, pp.6.4.1, 6.4.3
- ^ Dyer, p.480
Räisänen and Lehto, p.118-119
Naval Air Warfare Center, p.6.4.4 - ^ 20.0 20.1 Ishii, p.200
- ^ Ishii, pp. 229–230
Morgan, p. 150
Räisänen and Lehto, pp. 126–127 - ^ Ishii, p. 201
- ^ Räisänen and Lehto, pp. 122, 127
- ^ Reddy et al., pp.60, 71
Naval Air Warfare Center, pp.6.4.4, 6.4.5 - ^ Matthaei et al., pp.811–812
Ishii, pp.223–226 - ^ Ishii, p.202
Morgan, p.149 - ^ Ishii, pp.205–6, 209
Morgan, p.149
Räisänen and Lehto, pp.122–123 - ^ Ishii, p.211
- ^ Ishii, pp.211–212
- ^ Ishii, pp.212–213
- ^ Morgan, p.149
- ^ Naval Air Warfare Center, p.6.4.4
Ishii, p.201
Räisänen and Lehto, pp.123–124 - ^ Hickman, pp.50–51
- ^ Bigelow et al., p.211
Chapuis and Joel, p.512 - ^ Vizmuller, pp.107–108
- ^ Vizmuller, p.108
- ^ Hickman, pp.49–50
- ^ Hickman, p.50
- ^ Bryant, pp.114–115
- ^ Naval Air Warfare Center, pp.6.4.2–6.4.3
- ^ Naval Air Warfare Center, pp.6.4.3–6.4.4
- ^ Chen, p.76
Gralla, pp.61-62 - ^ Naval Air Warfare Center, p.6.4.5
- ^ Naval Air Warfare Center, p.6.4.4
- ^ Fujimoto, pp.199–201
Lo and Lee, p.27.7
参考书目
[编辑]![]() 本条目引用的公有领域材料来自Avionics Department of the Naval Air Warfare Center Weapons Division的文档《Electronic Warfare and Radar Systems Engineering Handbook (report number TS 92-78)》 (查询于9 June 2006) (pp 6–4.1 to 6–4.5 Power Dividers and Directional Couplers)。
本条目引用的公有领域材料来自Avionics Department of the Naval Air Warfare Center Weapons Division的文档《Electronic Warfare and Radar Systems Engineering Handbook (report number TS 92-78)》 (查询于9 June 2006) (pp 6–4.1 to 6–4.5 Power Dividers and Directional Couplers)。
- Stephen J. Bigelow, Joseph J. Carr, Steve Winder, Understanding telephone electronics Newnes, 2001 ISBN 0-7506-7175-0.
- Geoff H. Bryant, Principles of Microwave Measurements, Institution of Electrical Engineers, 1993 ISBN 0-86341-296-3.
- Robert J. Chapuis, Amos E. Joel, 100 Years of Telephone Switching (1878–1978): Electronics, computers, and telephone switching (1960–1985), IOS Press, 2003 ISBN 1-58603-372-7.
- Walter Y. Chen, Home Networking Basis, Prentice Hall Professional, 2003 ISBN 0-13-016511-5.
- Stephen A. Dyer, Survey of instrumentation and measurement Wiley-IEEE, 2001 ISBN 0-471-39484-X.
- Kyōhei Fujimoto, Mobile Antenna Systems Handbook, Artech House, 2008 ISBN 1-59693-126-4.
- Preston Gralla, How the Internet Works, Que Publishing, 1998 ISBN 0-7897-1726-3.
- Ian Hickman, Practical Radio-frequency Handbook, Newnes, 2006 ISBN 0-7506-8039-3.
- Thomas Koryu Ishii, Handbook of Microwave Technology: Components and devices, Academic Press, 1995 ISBN 0-12-374696-5.
- Y. T. Lo, S. W. Lee, Antenna Handbook: Applications, Springer, 1993 ISBN 0-442-01594-1.
- Matthaei, George L.; Young, Leo and Jones, E. M. T. Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964 OCLC 299575271
- D. Morgan, A Handbook for EMC Testing and Measurement, IET, 1994 ISBN 0-86341-756-6.
- Antti V. Räisänen, Arto Lehto, Radio engineering for wireless communication and sensor applications, Artech House, 2003 ISBN 1-58053-542-9.
- K.R. Reddy, S. B. Badami, V. Balasubramanian, Oscillations And Waves, Universities Press, 1994 ISBN 81-7371-018-X.
- Peter Vizmuller, RF design guide: systems, circuits, and equations, Volume 1, Artech House, 1995 ISBN 0-89006-754-6.



























