功率分配器與定向耦合器


功率分配器與定向耦合器是主要用於無線電或微波領域的被動元件。它們將傳輸線中的電磁功率耦合到端口,使得信號能夠用在另一個電路中。定向耦合器的一個基本特徵是它們只將電磁功率耦合到固定的方向。在兩個端口平均分配功率的定向耦合器又稱為混合耦合器。
定向耦合器最常由兩個耦合的傳輸線構成,這兩個傳輸線足夠靠近,使得其中一個的能量能耦合到另一個。這種技術在微波頻率上是有利的,其中傳輸線設計通常用於實現許多電路元件。然而,集中式組件也可以在較低頻率下使用,例如電話中遇到的音頻頻率。同樣在微波頻率,特別是較高頻帶,可以使用波導設計。這些波導耦合器中的許多對應於導電傳輸線設計中的一個,但是也存在波導特有的類型。
定向耦合器和功率分配器有許多應用。這些包括提供用於測量或監視的信號樣本、反饋、組合來自天線的饋送、天線波束成形,為諸如有線電視的有線分佈式系統提供分接頭,以及在電話線上分離發送和接收信號。
符號
[編輯]

最常用於定向耦合器的符號如圖1所示。符號可以在其上標記以dB為單位的耦合因子。定向耦合器有四個端口。端口1是應用電源的輸入端口。端口3是耦合端口,其中出現應用於端口1的一部分功率。端口2是輸出端口1的電源輸出的端口,少於端口3的輸出端口。定向耦合器通常是對稱的,因此也存在端口4,即隔離端口。施加到端口2的一部分功率將耦合到端口4.但是,該設備通常不用於此模式,端口4通常以匹配負載(通常為50歐姆)終止。 該終止可以在設備內部,並且用戶不能訪問端口4。實際上,這導致3端口設備,因此圖中的定向耦合器的第二符號的效用[1]。
「端口a處的參數P由於端口b處的輸入」。
功率分配器的符號如圖2所示。功率分配器和定向耦合器都屬於同一類器件。定向耦合器通常是較少耦合的4端口器件,只有一小部分輸入功率出現在耦合端口上。功率分配器則相反,多數功率能到達輸出端口,常被視為三端口器件。[2]
參數
[編輯]當其他端口都匹配負載時,所有定向耦合器所需的共同特性是較大的帶寬、高定向性和所有端口的良好阻抗匹配[3]。
耦合系數
[編輯]耦合系數的定義為:
其中P1是端口1的輸入功率,P3是耦合端口3的輸出功率。
耦合系數是定向耦合器的主要特性參數。它是負數的,對於無源器件不能超過0 dB,並且通常小於−3 dB ,因為輸出功率不可能比輸入功率多。在其他文獻裏,常會省略負號,甚至定義為正數[4] 。
耦合系數會隨着頻率而變化。雖然不同的設計可以減少方差,但理論上不能構建完美平坦的耦合器。定向耦合器是根據頻帶中心的耦合精度來規定的。[5]
損失參數
[編輯]
從端口1到端口2的插入損失(P1 – P2) 是:
插入損失:
部分損失是由於某些功率進入耦合端口而被稱為耦合損失,由下式給出:
耦合損失:
理想定向耦合器的插入損耗完全由耦合損耗組成。理想定向耦合器的插入損耗完全由耦合損耗組成。然而,實際定向耦合器中,插入損耗包括耦合損失、電介質損失,導體損失和駐波比損失。根據頻率範圍,耦合損耗在 15 dB耦合之上變得不那麼顯著,其他損耗構成總損耗的大部分。耗散耦合器的理論插入損失(dB)與耦合(dB)的關係如圖3和下表所示。[6]
| 耦合系數 | 插入損失 |
|---|---|
| dB | dB |
| 3 | 3.00 |
| 6 | 1.25 |
| 10 | 0.458 |
| 20 | 0.0436 |
| 30 | 0.00435 |
隔離度
[編輯]定向耦合器的隔離度可以定義為當其他兩個端口由匹配負載時,輸入端口和隔離端口之間的信號能差(以dB為單位)。隔離度定義如下式:
也可以在兩個輸出端口之間定義隔離。在這種情況下,其中一個輸出端口用作輸入; 另一個被認為是輸出端口,而另外兩個端口(輸入和隔離)則匹配負載。因此定義如下:
輸入端口和隔離端口之間的隔離可能與兩個輸出端口之間的隔離不同。 例如,端口1和4之間的隔離可以是 30 dB,而端口2和3之間的隔離可以是不同的值,例如 25 dB。 可以從耦合加上回波損耗估算隔離。 隔離度應盡可能高。 在實際的耦合器中,隔離端口永遠不會完全隔離。 一些射頻功率將始終存在。 波導定向耦合器將具有最佳隔離度。[6]
定向性
[編輯]定向性與隔離直接相關。 它被定義為:
其中: P3是耦合端口的輸出功率,P4是隔離端口的功率輸出。
定向性越高越好。定向性隨頻率改變而變化,並且在設計的頻率點上特別高。定向性對頻率特別敏感,因為它是兩個波分量的差。波導定向耦合器將具有最佳定向性。定向性無法直接測量,需要通過增加隔離度和耦合系數測量來計算:[7]
如果使用正的耦合系數,則公式改為:
散射參數
[編輯]理想無限隔離與完全匹配且對稱定向耦合器的散射參數由下式給出,
- 是傳輸系數。
- 是耦合系數。
通常與都是複數,並且隨頻率變化。矩陣主對角線上0代表阻抗匹配,任何端口的功率輸入都不會反射回同一個端口。在反對角線上,0代表輸入和隔離端口之間完美隔離。
對於無源無損定向耦合器,其矩陣為么正矩陣:
因為進入輸入端口的能量必須全部由其他兩個端口之一離開。[8]
插入損失與相關;
耦合系數與相關;
主對角線上飛零代表有回波損失;反對角線上非零則代表隔離不完全。然而,部分作者定義了端口號3和4互換的端口號。這導致散射矩陣在反對角線上不再是全零。[9]
幅度平衡
[編輯]幅度平衡指的是3dB混合器的兩個輸出端口之間的功率差異(dB)。在理想的功率平分器中,其差值應為0dB。 然而,實際上,幅度平衡取決於頻率並且偏離理想的0dB[7]。
相位平衡
[編輯]相位平衡定義為兩個輸出段口的相位差。理想情況,混合耦合器的兩個輸出端口之間的相位差應為0°,90°或180°。然而,與幅度平衡一樣,相位差依輸入頻率而變化[7]。
傳輸線模型
[編輯]定向耦合器
[編輯]耦合傳輸線
[編輯]
定向耦合器的最常見形式是一對耦合傳輸線。它們可以通過多種技術實現,包括同軸和平面技術(微帶線與帶狀線)。圖4中的四分之一波長(λ/ 4)定向耦合器為帶狀線。耦合線上的功率以與主線上的功率呈反方向流動,因此端口佈置與圖1中所示的不同,但編號保持相同。因此,它有時被稱為「後向耦合器」。[10]
端口1與端口2之間是「主線」;端口3與端口4之間是「耦合線」。由於定向耦合器是線性器件,因此圖1中的符號是任意的。任何端口都可以是輸入端(如圖20所示),這將導致直接連接的端口是傳輸端口,相鄰端口是耦合端口,對角端口是隔離端口。在一些定向耦合器上,主線設計用於高功率操作(大型連接器),而耦合端口可以使用小型連接器,例如SMA連接器。內部負載額定功率也可能限制耦合線路上的操作。[3]

耦合系數的精度取決於兩條耦合線間距的尺寸公差。對於平面印刷技術,這取決於印刷過程的解像度,決定了可以產生的最小軌道寬度,並且還限制兩條線的間距。當需要非常緊密的耦合併且經常使用不同的設計 3dB的耦合器時,這成為一個問題。然而,可以在空氣帶狀線中生產緊密耦合的線,這也允許通過印刷平面技術製造。在這種設計中,兩條線印刷在電介質的「相對」側面而不是並排。兩條線在它們的寬度上的耦合遠大於它們彼此邊緣接合時的耦合。 [11]
λ/ 4耦合線設計適用於同軸和帶狀線實現,但在現在流行的微帶格式中不能很好地工作,儘管設計確實存在。原因是微帶不是均勻介質 - 傳輸帶上方和下方有兩種不同的介質。這導致除了導電電路中常見的TEM模式之外的橫向模式。偶模和奇模的傳播速度不同,導致信號色散。微帶線的更好解決方案是比λ/ 4短得多的耦合線,如圖5所示,但這具有耦合因子隨頻率顯著上升的缺點。有時遇到的這種設計的變型使得耦合線具有比主線更高的特性阻抗,如圖6所示。這種設計在將耦合器饋送到用於功率監測的檢測器的情況下是有利的。對於給定的主線功率,較高阻抗線導致較高的射頻電壓,使得檢測器二極管的工作更容易[12]。
製造商規定的頻率範圍是耦合線的頻率範圍。主線響應要寬得多:例如, 2-4 GHz指定的耦合器可能有一條可以在 1-5 GHz運行的主線。主線響應要寬得多:例如, 2-4 GHz指定的耦合器可能有一條可以在 1-5 GHz運行的主線。 與所有分佈式元件電路一樣,耦合響應是頻率週期性的。 例如,λ/ 4耦合線耦合器將在nλ/ 4處具有響應,其中n是奇整數。[3]
單個λ/ 4耦合部分適用於小於八度的帶寬。 為了獲得更大的帶寬,使用多個λ/ 4耦合部分。 這種耦合器的設計與分佈式元件濾波器的設計大致相同。 耦合器的各部分被視為濾波器的部分,通過調整每個部分的耦合系數,可以使耦合端口具有任何經典濾波器響應,例如最大平坦(巴特沃斯濾波器), 等紋波(橢圓函數濾波器)或指定紋波(切比雪夫濾波器)響應。 紋波濾波器是通帶中耦合端口輸出的最大變化,通常用標稱耦合因子作為正或負的dB值[13]。

可以看出,耦合線定向耦合器的純實數,而在所有頻率上都是純虛數的。這導致S矩陣的簡化以及耦合端口始終與輸出端口處於正交相位相位(90°)的結果。一些應用程序利用這種相位差。 讓,無損操作的理想情況簡化為[14]:
分支線耦合器
[編輯]
分支線耦合器由兩條物理耦合在一起的並行傳輸線組成,它們之間有兩條或多條支路。分支線間隔λ/ 4並且以與耦合線耦合器的多個部分相同的方式表示多部分濾波器設計的部分,除了這裏每個部分的耦合由分支線的阻抗控制。主線和耦合線是系統阻抗的。耦合器中的部分越多,分支線的阻抗比越高。高阻抗線具有窄軌道,並且由於製造限制,這通常將設計限制為平面格式的三個部分。類似的限制適用於比 10 dB寬鬆的耦合因子;低耦合也需要窄軌道。當需要鬆耦合時,耦合線是更好的選擇,但分支線耦合器適用於緊耦合,可用於 3 dB混合。分支線耦合器通常不具有如耦合線那樣寬的帶寬。這種類型的耦合器適用於高功率、空氣介電、實心棒形式,因為剛性結構易於機械支撐。[15]
藍澤耦合器
[編輯]藍澤耦合器的結構類似於交叉指形濾波器,並行的線路交錯以實現耦合。它用於 3 dB到 6 dB範圍內的強耦合[16]。
功率分配器
[編輯]
最早的傳輸線功率分配器是簡單的T型接頭。它們在輸出端口之間的隔離非常差,從端口2反射出來的功率很多都會進入端口3。三端口網絡不能同時達到「無損」、端口匹配負載、「互易」。然而,這四端口網絡可以達到這些條件,可以設計四端口設備,使到達端口2的功率在端口1之間分配,端口4以匹配負載,端口3隔離。[17]
術語「混合耦合器」最初應用於3 dB耦合線定向耦合器,即其中兩個輸出均為輸入功率的一半。 這同義詞意味着正交 3dB耦合器,輸出相位相差90°。 現在任何帶有隔離端和相等功率分配的匹配4端口稱為混合耦合器。 其他類型可以具有不同的相位關係。 如果為90°,則為90°混合,如果為180°,則為180°混合等。在本文中,沒有限定條件的「混合耦合器」意味着耦合線混合。[18]
威爾金森功率分配器
[編輯]
威爾金森功率分配器由兩個並聯的非耦合λ/4傳輸線組成。輸入並行饋送到兩條線路,輸出端接兩圈的系統阻抗。該設計可以採用平面格式實現,但它在同軸電纜中具有更自然的實現:在平面中,兩條線必須保持分開,這樣它們不會耦合,而是必須在它們的輸出端匯集在一起,這樣它們就可以被端接而不是在同軸電纜中,線路可以依靠同軸外導體並排運行以進行篩選。
威爾金森功率分配器解決了簡單T型接頭的匹配問題:它在所有端口具有低電壓駐波比,在輸出端口之間具有高隔離度。每個端口的輸入和輸出阻抗設計為等於微波系統的特徵阻抗。這是通過使系統阻抗的線阻抗 來實現的 - 對於50Ω系統,威爾金森線約為70 Ω。[19]
混合耦合器
[編輯]上面描述了耦合線定向耦合器。當耦合設計為 3dB時,它被稱為混合耦合器。理想的對稱混合耦合器的S矩陣減少到:
兩個輸出端口具有90°相位差(-「i」至-1),因此這是90°混合。[20]
混合環型耦合器
[編輯]
混合環型耦合器,也稱為鼠標耦合器,是一個四端口 3dB定向耦合器,由一個3λ/ 2環形傳輸線組成,其中四條線的間隔為如圖12所示。端口1處的電源輸入在環上分開並雙向傳播。在端口2和3處,信號同相到達並且在端口4處增加,但是它是異相所以被消除。端口2和3彼此同相,因此這是0°混合的示例。圖12示出了平面實現,但是該設計也可以在同軸或波導中實現。通過使環的每個λ/ 4部分交替地低和高阻抗,但是對於 3dB耦合器,可以產生具有與 3dB不同的耦合因子的耦合器。 環是的端口阻抗,對於50Ω設計,環大約為70Ω[21]。
混合環型耦合器的S參數矩陣為:
混合環的端口不對稱;選擇不同輸入端口不一定產生相同的結果。從端口1或端口3輸入,混合環是如所述的0°混合。但是,輸入端口2或端口4會產生180°混合。[22]
這一事實導致混合環的另一個有用的應用:它可用於從兩個輸入信號產生和(Σ)和差(Δ)信號,如圖12所示。對於端口2和3的輸入,出現Σ信號在端口1處,Δ信號出現在端口4處[23]。
多輸出分頻器
[編輯]
典型的功率分配器如圖13所示。理想情況下,輸入功率將在輸出端口之間平均分配。分頻器由多個耦合器組成,與耦合器一樣,可以反轉並用作多工器。缺點是對於四通道多路復用器,輸出僅由每個功率的1/4組成,並且效率相對較低。其原因在於,在每個組合器的一半輸入功率到達端口4並在終端負載中耗散。如果兩個輸入是相干,則可以安排相位,使得在端口4處發生消除,然後所有功率將轉到端口1。但是,多路復用器輸入通常來自完全獨立的源,因此不連貫。無損多路復用只能通過濾波器網絡完成。[24]
波導類型
[編輯]波導定向耦合器
[編輯]波導分支線耦合器
[編輯]上述波導分支線耦合器也可以在波導中實現。[25]
倍茲孔方向耦合器
[編輯]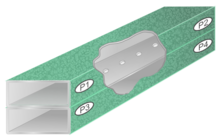
倍茲孔方向耦合器是最常見、最簡單的波導定向耦合器之一。 它由兩個平行的波導組成,一個堆疊在另一個的頂部,在它們之間有一個孔。一個導向裝置的一些功率通過孔進入另一個導向裝置。倍茲孔方向耦合器是後向耦合器的另一個例子。[26]
倍茲孔方向耦合器的概念可以通過提供多個孔來擴展。孔間隔λ/ 4。這種耦合器的設計與多段耦合傳輸線相似。使用多個孔可以通過將這些部分設計為巴特沃斯、契比雪夫或其他一些濾波器類來擴展帶寬。選擇孔尺寸以為過濾器的每個部分提供所需的耦合。設計標準是在所需頻帶上實現基本上平坦的耦合以及高方向性[27]。
瑞雷特短槽藕合器
[編輯]瑞雷特短槽藕合器是兩個波導並排,側壁是共同的,而不是像倍茲孔方向耦合器那樣的長邊。在側壁上切出一個槽以允許耦合。這種設計經常用於產生 3dB耦合器。[28]
施溫格反相耦合器
[編輯]施溫格反相耦合器是另一種使用平行波導的設計,這次一側的長邊與另一側的短側壁相同。 在間隔λ/ 4的波導之間切割兩個偏心槽。施溫格是一個後向耦合器。與Bethe-hole耦合器相比,這種設計具有基本上平坦的方向性響應和與頻率相關的強耦合的缺點,倍茲孔方向耦合器的耦合因子幾乎沒有變化。[29]
莫侖諾十字形波導耦合器
[編輯]莫侖諾十字形波導耦合器有兩個波導,一個堆疊在另一個上面,像倍茲孔方向耦合器,但彼此成直角而不是平行。在波導之間的對角線上切割兩個通常為十字形的偏心孔,距離分開。莫侖諾十字形波導耦合器適用於緊耦合應用。 這是倍茲孔方向耦合器和莫侖諾耦合器的特性之間的折衷,其耦合和方向性隨頻率而變化。[30]
波導功率分配器
[編輯]波導混合環
[編輯]上面討論的波導混合環也可以在波導中實現。[31]
幻T形接頭
[編輯]
首先通過簡單的T形接頭完成相干功率分配。 在微波頻率下,波導三通有兩種可能的形式:E與H平面。這兩個結均等地分配功率,但由於結處的場結構不同,輸出臂處的電場與H平面三通同相,並且對於E平面三通為180°異相。 這兩個發球枱的組合形成混合發球枱被稱為魔T。魔T是一個四端口組件,可以執行兩個相干微波信號的向量和(Σ)和差值(Δ)。[32]
集總元件
[編輯]混合變壓器
[編輯]
標準的3dB混合變壓器如圖16所示。端口1的電源在端口2和3之間平均分配,但相互反相。因此,混合變壓器是180°混合動力。中心抽頭通常在內部端接,但可以將其作為端口4引出; 在這種情況下,混合可以用作和和混合。但是,端口4表示與其他端口不同的阻抗,如果需要在相同的系統阻抗下使用該端口,則需要額外的變壓器進行阻抗轉換。[33]
混合變壓器通常用於電信中,用於2到4線轉換。電話手機包括這樣的轉換器,用於將2線線路轉換為來自耳機和吹嘴的4線。[34]
交叉連接變壓器
[編輯]
對於較低的頻率(小於 600 MHz),可以通過RF變壓器實現緊湊的寬帶實現。在圖17中,示出了用於弱耦合的電路,並且可以沿着這些線理解:信號進入一個線對。一個變壓器降低信號電壓,另一個變壓器降低電流。因此,阻抗匹配。相同的論證適用於通過耦合器的信號的每個其他方向。感應電壓和電流的相對符號決定了輸出信號的方向[35]。
耦合由下式給出:
其中n是次級匝數比。
對於 3 dB耦合,即在發送端口和耦合端口之間信號的相等分割,,並且隔離端口以兩次終止 50Ω系統的特徵阻抗 - 100Ω。基於該電路的 3dB功率分配器具有彼此180°相位的兩個輸出,與具有90°相位關係的λ/ 4耦合線相比。[36]
電阻性T形接頭
[編輯]
簡單電阻性T形電路可用作功率分配器,如圖18所示。通過Y-Δ變換,該電路也可以實現為Δ電路。使用增量形式電阻器等於系統阻抗。這可能是有利的,因為系統阻抗值的精密電阻器總是可用於大多數係統標稱阻抗。 三通電路具有簡單,低成本和本質上寬帶寬的優點。 它有兩個主要缺點; 首先,電路將耗散功率,因為它是電阻性的:相等的分裂將導致 6 dB插入損耗而不是 3 dB。 第二個問題是 0 dB方向性導致輸出端口之間的隔離非常差。[37]
對於不均等的功率分配,插入損耗不是問題:例如端口3處的 -40 dB在端口2處具有小於 0.2 dB的插入損耗。隔離可以是通過用T pad s替換輸出電阻,以兩個輸出端口的插入損耗為代價進行了改進。 隔離改善大於增加的插入損耗。[38]
6dB電阻橋式混合電路
[編輯]
真正的混合分配器/耦合器理論上可以通過電阻橋電路實現無限隔離和方向性。與三通電路一樣,電橋具有 6 dB插入損耗。它的缺點是不添加變壓器就不能用於不平衡電路; 但是,如果插入損耗不是問題,它是600Ω平衡通信線路的理想選擇。橋中代表端口的電阻器通常不是器件的一部分(端口4除外,它可能在內部永久端接),這些電阻由線路終端提供。因此,該裝置基本上由兩個電阻器(加上端口4終端)組成[39]。
應用
[編輯]監測
[編輯]定向耦合器的耦合輸出可用於監視信號的頻率和功率電平,而不會中斷系統中的主要功率流(功率降低除外,見圖3)[3]。
利用隔離
[編輯]
如果隔離度很高,定向耦合器有利於組合信號以將單線饋送到接收器以進行雙音接收機測試。在圖20中,一個信號進入端口P3,一個進入端口P2,而兩個出口P1。從端口P3到端口P1的信號將經歷 10 dB的丟失,並且來自端口P2的信號到端口P1將失去 0.5 dB。隔離端口上的內部負載將消除端口P3和端口P2的信號損耗。如果忽略圖20中的隔離器,則隔離測量(端口P2到端口P3)確定來自信號產生器 的功率量F2將被注入信號發生器 F1。隨着注入水平的增加,它可能導致信號發生器F1的調製,甚至注入鎖相。由於定向耦合器的對稱性,反向注入將發生與F1的信號發生器F2相同的可能調製問題。因此,在圖20中使用隔離器以有效地增加定向耦合器的隔離(或方向性)。因此,注入損耗將是定向耦合器的隔離加上隔離器的反向隔離[40]。
混合電路
[編輯]混合電路的應用包括單脈衝比較器、頻率混頻器、功率合成器、分頻器、調製器和相控陣雷達天線系統。兩個同相設備(例如威爾金森分頻器)和正交(90°)混合耦合器可用於相干功率分配器應用。[41]
在家中使用便宜版本的功率分配器將有線電視或無線電視信號分配給多個電視機和其他設備。具有兩個以上輸出端口的多端口分離器通常由多個級聯耦合器內部組成。域內寬帶互聯網服務可由有線電視公司提供(有線互聯網)。域內用戶的互聯網電纜調製解調器連接到分離器的一個端口[42]。
功率合成器
[編輯]由於混合電路是雙向的,因此它們可以用於相干地組合功率以及分離功率。在圖21中,示出了分離以饋送多個低功率放大器的信號的示例,然後重新組合以饋送具有高功率的單個天線[2]。


每個功率組合器的輸入的相位被佈置成使得兩個輸入彼此異相90°。由於混合組合器的耦合端口與發送端口成90°異相,這導致功率在組合器的輸出處相加並在隔離端口處抵消:圖22中的代表性示例在圖22中示出。注意,每個組合器/分配器的兩個端口都有一個額外的固定90°相移,為簡單起見,圖中未示出[20] 。
對兩個輸入端口施加同相功率將無法獲得所需的結果:兩個輸入端的正交總和將出現在兩個輸出端口:這是每個輸出端口總功率的一半。這種方法允許在電路中使用許多更便宜和更低功率的放大器而不是單個高功率行波管。另一種方法是讓每個固態放大器(SSA)饋送天線並使功率在空間中組合或用於饋送連接到天線的鏡頭[43]。
相位差
[編輯]
90°混合耦合器的相位特性可用於微波電路中的巨大優勢。 例如,在平衡微波放大器中,兩個輸入級通過混合耦合器饋電。 場效應電晶體器件通常具有非常差的匹配並且反射大部分入射能量。然而,由於器件基本相同,因此來自每個器件的反射系數相等。來自FET的反射電壓在隔離端口處同相,並且在輸入端口處為180°不同。因此,來自FET的所有反射功率都會進入隔離端口的負載,並且沒有電源進入輸入端口。這導致良好的輸入匹配(低駐波比)。[7]
如果相位匹配線用於180°混合耦合器的天線輸入,如圖23所示,則零點將直接出現在天線之間。要在該位置接收信號,必須改變混合類型或線路長度。 要拒絕來自給定方向的信號,或為單脈衝雷達創建差異模式,這是一種很好的方法[44]。
通過將相位延遲到天線陣列的下部元件,可以使用相位差耦合器在VHFFM 無線電台中創建波束傾斜。更一般地,相位差耦合器與固定相位延遲和天線陣列一起用於諸如巴特勒矩陣的波束形成網絡中,以在任何規定方向上創建無線電波束[45]。
參考文獻
[編輯]- ^ Ishii, p.200
Naval Air Warfare Center, p.6-4.1 - ^ 2.0 2.1 Räisänen and Lehto, p.116
- ^ 3.0 3.1 3.2 3.3 Naval Air Warfare Center, p.6.4.1
- ^ For instance; Morgan, p.149
- ^ Naval Air Warfare Center, p.6.4.1
Vizmuller, p.101 - ^ 6.0 6.1 Naval Air Warfare Center, p.6.4.2
- ^ 7.0 7.1 7.2 7.3 Naval Air Warfare Center, p.6.4.3
- ^ Dyer, p.479
Ishii, p.216
Räisänen and Lehto, pp.120–122 - ^ For instance, Räisänen and Lehto, pp.120–122
- ^ Morgan, p.149
Matthaei et al., pp.775–777
Vizmuller, p.101 - ^ Naval Air Warfare Center, p.6.4.1
Matthaei et al., pp.585–588, 776–778 - ^ Räisänen and Lehto, pp.124–126
Vizmuller, pp.102–103 - ^ Naval Air Warfare Center, p.6.4.1
Matthaei et al., pp.775–777 - ^ Ishii, p.216
Räisänen and Lehto, p.120-122 - ^ Ishii, pp.223–226
Matthaei et al., pp.809–811
Räisänen and Lehto, p.127 - ^ Räisänen and Lehto, p.126
- ^ Räisänen and Lehto, pp.117–118
- ^ Naval Air Warfare Center, pp.6.4.1, 6.4.3
- ^ Dyer, p.480
Räisänen and Lehto, p.118-119
Naval Air Warfare Center, p.6.4.4 - ^ 20.0 20.1 Ishii, p.200
- ^ Ishii, pp. 229–230
Morgan, p. 150
Räisänen and Lehto, pp. 126–127 - ^ Ishii, p. 201
- ^ Räisänen and Lehto, pp. 122, 127
- ^ Reddy et al., pp.60, 71
Naval Air Warfare Center, pp.6.4.4, 6.4.5 - ^ Matthaei et al., pp.811–812
Ishii, pp.223–226 - ^ Ishii, p.202
Morgan, p.149 - ^ Ishii, pp.205–6, 209
Morgan, p.149
Räisänen and Lehto, pp.122–123 - ^ Ishii, p.211
- ^ Ishii, pp.211–212
- ^ Ishii, pp.212–213
- ^ Morgan, p.149
- ^ Naval Air Warfare Center, p.6.4.4
Ishii, p.201
Räisänen and Lehto, pp.123–124 - ^ Hickman, pp.50–51
- ^ Bigelow et al., p.211
Chapuis and Joel, p.512 - ^ Vizmuller, pp.107–108
- ^ Vizmuller, p.108
- ^ Hickman, pp.49–50
- ^ Hickman, p.50
- ^ Bryant, pp.114–115
- ^ Naval Air Warfare Center, pp.6.4.2–6.4.3
- ^ Naval Air Warfare Center, pp.6.4.3–6.4.4
- ^ Chen, p.76
Gralla, pp.61-62 - ^ Naval Air Warfare Center, p.6.4.5
- ^ Naval Air Warfare Center, p.6.4.4
- ^ Fujimoto, pp.199–201
Lo and Lee, p.27.7
參考書目
[編輯]![]() 本條目引用的公有領域材料來自Avionics Department of the Naval Air Warfare Center Weapons Division的文檔《Electronic Warfare and Radar Systems Engineering Handbook (report number TS 92-78)》 (查詢於9 June 2006) (pp 6–4.1 to 6–4.5 Power Dividers and Directional Couplers)。
本條目引用的公有領域材料來自Avionics Department of the Naval Air Warfare Center Weapons Division的文檔《Electronic Warfare and Radar Systems Engineering Handbook (report number TS 92-78)》 (查詢於9 June 2006) (pp 6–4.1 to 6–4.5 Power Dividers and Directional Couplers)。
- Stephen J. Bigelow, Joseph J. Carr, Steve Winder, Understanding telephone electronics Newnes, 2001 ISBN 0-7506-7175-0.
- Geoff H. Bryant, Principles of Microwave Measurements, Institution of Electrical Engineers, 1993 ISBN 0-86341-296-3.
- Robert J. Chapuis, Amos E. Joel, 100 Years of Telephone Switching (1878–1978): Electronics, computers, and telephone switching (1960–1985), IOS Press, 2003 ISBN 1-58603-372-7.
- Walter Y. Chen, Home Networking Basis, Prentice Hall Professional, 2003 ISBN 0-13-016511-5.
- Stephen A. Dyer, Survey of instrumentation and measurement Wiley-IEEE, 2001 ISBN 0-471-39484-X.
- Kyōhei Fujimoto, Mobile Antenna Systems Handbook, Artech House, 2008 ISBN 1-59693-126-4.
- Preston Gralla, How the Internet Works, Que Publishing, 1998 ISBN 0-7897-1726-3.
- Ian Hickman, Practical Radio-frequency Handbook, Newnes, 2006 ISBN 0-7506-8039-3.
- Thomas Koryu Ishii, Handbook of Microwave Technology: Components and devices, Academic Press, 1995 ISBN 0-12-374696-5.
- Y. T. Lo, S. W. Lee, Antenna Handbook: Applications, Springer, 1993 ISBN 0-442-01594-1.
- Matthaei, George L.; Young, Leo and Jones, E. M. T. Microwave Filters, Impedance-Matching Networks, and Coupling Structures McGraw-Hill 1964 OCLC 299575271
- D. Morgan, A Handbook for EMC Testing and Measurement, IET, 1994 ISBN 0-86341-756-6.
- Antti V. Räisänen, Arto Lehto, Radio engineering for wireless communication and sensor applications, Artech House, 2003 ISBN 1-58053-542-9.
- K.R. Reddy, S. B. Badami, V. Balasubramanian, Oscillations And Waves, Universities Press, 1994 ISBN 81-7371-018-X.
- Peter Vizmuller, RF design guide: systems, circuits, and equations, Volume 1, Artech House, 1995 ISBN 0-89006-754-6.



























