频率 (物理学)

频率(frequency)又称周率,是物理学上描述某具规律周期性的现象或事件,在每单位时间内(即每秒)重复发生的次数(周期数,即循环次数);通常以符号 或 表示。频率的单位采用国际单位制,为赫兹(德语:Hertz,简写为 Hz)[注 1]。
设 时间内某事件重复发生 次,则此事件发生的频率为:
- 赫兹
又因为周期定义为重复事件发生的最小时间间隔,故频率也可以表示为周期()的倒数:
- 赫兹
为了方便起见,较长较慢的波,像海洋表面的面波,通常是以周期(单位:秒)来描述其波动性质。较短较快的波,像声波和无线电波,通常是以频率(单位:秒-1)来描述其波动性质。
在国际单位制里,频率的单位——赫兹是以德国物理学家海因里希·赫兹(德语: Heinrich Rudolf Hertz , 1857年2月22日-1894年1月1日)而命名[1]。1赫兹(Hz)表示事件每一秒发生一次。
除非特别声明,频率一般是指单位时间内周期数的时间频率(temporal frequency),相对于单位长度内周期数的空间频率(spatial frequency)。其他用来表示频率的单位还有:旋转机械器材领域采用的传统衡量单位为每分钟转速(rpm)等;医学上,心率以“次/分钟”(bpm)为单位[2],而呼吸频率则可以“周期/分钟”(cpm)为单位。
测量方法
[编辑]
数算法
[编辑]通过数算在某时间间隔内重复事件发生的次数,就可以获得这重复事件发生的频率:
例如,假若在15秒内发生了71次,则频率为
- Hz
另一种方法是测量这重复事件发生设定次数所需要的时间间隔[3]。不过此方法在计数次数介于零和一次之间时,计数次数会有随机误差,会造成计算频率会有 的误差,
其中
- 为取样间隔
- 为量测到的频率
其误差会随著频率而递减,因此信号在低频率,而取样到的次数又小,就会出现类似的问题。例如每秒量测一次频率0.5Hz(即每两秒一个周期)的信号,量到的次数会在一次和零次之间变化,需要取平均后才能得到真实的频率。
频闪观测器
[编辑]频闪观测器可以用来测量旋转物体或振动物体的频率。频闪观测器会发射出重复地强烈闪光(频闪光),其频率可以用校准计时电路来调整。将频闪光对准于旋转物体或振动物体,然后调整闪烁频率。当频闪光的频率等于旋转频率或振动频率时,这物体会在每次频闪光闪烁的时候,正好完成一个循环,回到同样位置。所以,这物体看起来好像固定不动[4]。这物体的运动频率可以从频闪观测器的读出装置获得。请注意,假若这物体的运动频率是闪烁频率的整数倍数,则这物体也会看起来好像固定不动。
频率计数器
[编辑]频率计数器是一种电子仪器,可以用来测量较高频率。频率计数器专门测量重复性电子信号。它使用数位逻辑和准确石英计时器来数算在某时间间隔内的信号重复次数。不具有电子属性的循环过程,像转轴的旋转速率、机械振动、声波,可以用换能器转换为重复性电子信号。
外差法
[编辑]
假若电磁信号的频率超过频率计数器的适用域,则可以使用外差法。首先,在未知频率的附近,选择一个已知频率的参考信号,然后,使用二极体将两个信号混杂在一起,这会造成一个混杂拍信号,其频率为已知频率与未知频率的差值,称为拍频或差频,可以用频率计数器测量[5] 。当然这方法只能测量两个信号的频率的频差,要获得未知频率,必须使用其他方法先知道参考信号的频率。欲想测量更高频率,必须经过几个阶段的外差法。最新研究已经将这方法推展至红外线和可见光频率。
波的频率
[编辑]衡量声音、电磁波(例如无线电波或者光)、电讯信号或者其他波的频率时,表示每秒波形重复的数量。如果波是声音,频率衡量音符的特性。
当波从一种介质传入另一种介质,频率不变,而波长和相速度会变[6]。
若一波源和观察者之间有相对运动时,观察者接受到波的频率与波源发出的频率会不相同,此现象称为多普勒效应[7],例如当警车靠近观察者时,观察者接收到警车的频率会比警车发出的频率要高。
物理光学
[编辑]
辐射能(英语:radiant energy)是电磁波传播的能源。太阳或电光源都是辐射能的源头。人类的光学感测器(眼睛)能够分辨的光波称为可见光,是由几种颜色(红、橙、黄、绿、蓝、靛、紫)组成;其中每一种颜色都有特定的频带(英语:frequency band)。可见光在整个电磁辐射的频谱中只占有一小部分。紫外线(UV)的波长小于可见光,无法以肉眼看到;又红外线(IR)的波长大于可见光,也必须利用夜视镜和其他热感测设备才能观测得到。小于紫外线波长的电磁辐射有X射线和伽玛射线。大于红外线波长的有微波和无线电波,频带为兆赫和千赫,以及频带为毫赫和微赫的自然波。频率为2毫赫的波,其波长大约等于从地球到太阳的距离。微赫波的波长大约为0.0317 光年。奈米赫波的波长大约为31.6881光年。
按照波长长短,从长波开始,电磁波可以分类为电能、无线电波、微波、红外线、可见光、紫外线、X-射线和伽马射线等等。普通实验使用的光谱仪就足以分析从2 奈米到2500 奈米波长的电磁波。使用这种仪器,可以得知物体、气体或甚至恒星的详细物理性质。这是天文物理学的必备仪器。例如,因为超精细分裂(英语:hyperfine splitting),氢原子会发射波长为21.12公分的无线电波[8]。
人类眼睛可以观测到波长大约在400 奈米和700 奈米之间的电磁辐射,称为可见光[9]。
物理声学
[编辑]声音是传播于固体、液体、气体、等离子体的振动,尤其是指那些人耳能感受到的频率的振动。对于人类,听觉频率范围限制在大约20赫兹到2万赫兹(20千赫)之间,上限通常会随著年龄而减低。其他物种有不同的听觉频率范围。例如,有些犬种能感觉到高至45,000赫兹的振动[10]。声音是被许多物种用来做为感觉危险(英语:detect danger)、导航、掠食和通讯的主要感官之一。
凡是被诠释为声音的机械振动,都能够穿越处于各种物态的物质。这些能够传播声音的物质称为介质。声音不能传播于真空[11]。
信号、系统和频域
[编辑]
周期性的信号均有其对应的频率,而且可以透过傅立叶级数转换为不同频率弦波的和。而大部份信号(周期性或非周期性)可以用傅里叶变换转换成在不同频率下对应的振幅及相位,此种考虑信号或系统频率相关部份的分析方式称为频域。
许多物理元件的特性会随著输入讯号的频率而改变,例如电容在低频时阻抗变大,高频时阻抗变小,而电感恰好相反,高频时阻抗变大,低频时阻抗变小。一个线性非时变系统的特性也会随频率而变化,因此也有其频域下的特性,频率响应是输入振幅相同,频率不同的弦波,将各频率输出的振幅和相位相对频率绘制成图,可以显示一个系统频域下的特性。
有些系统的定义是以频域为准,例如低通滤波器只允许低于一定频率的讯号通过[12]。
不同国家交流电的标准频率
[编辑]欧洲、非洲、澳洲、南美洲的南部、亚洲的大部分区域、日本东部、中国大陆及俄国,这些地区的交流电频率都是50 Hz(接近于科学音调记号法下的音符G1,是低三个八度的G);而北美洲、南美洲的北部、日本西部、朝鲜半岛、菲律宾及台湾,这些地区都使用60Hz交流电[13](大约在音符B♭1与B1之间)。依据在不同地区所使用的交流电频率,在进行录音的同时所纪录下来的交流声[14]可以显露出进行录音的位置,例如在欧洲或北美洲。
其它种频率
[编辑]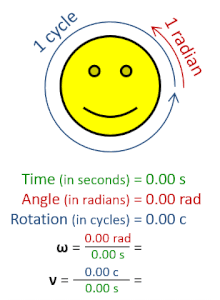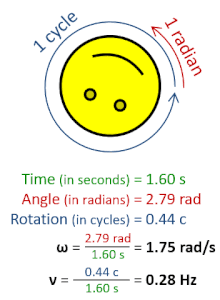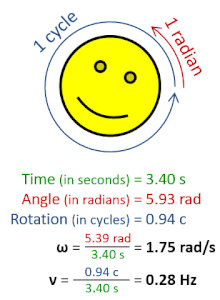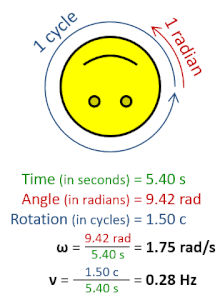
- 其中, 是角位移, 是时间。
- 空间频率类比时间频率,其时间轴替代为一条或多条空间轴。
备注
[编辑]- ^ 频率以往被含糊地俗称为:“周波数”或“周波”,这是因为在1960年代以前,电磁波被广播电台不精确的计量单位称作“周波(数)”,简称“周”,英语 cycles(Cy./Cyc.),实际上是指 cycles per second(cps),每秒周期数或振荡次数。而“周波”实际上是指具周期性的波动,例如无线电波或电磁波,其振荡从某点开始,完成一个过程后,再回到此点,称为一个周波。 例如:某无线电是 500周波,就是指频率为 500Hz的电磁波,而当时写作 500C,并非较正确的 500cps;又如某电台的“周率”是六十千周(60kc)这种写法,是指低频长波的频率为 60kHz。 1965年时,国际无线电协会决议,将电磁波的计量单位由周波改为赫,Hz 即为明确的 cps,而非含糊的 cycles ,而这一改变就是为了纪念赫兹在电磁波方面的发明创造。
参考文献
[编辑]- ^ 海因里希·鲁道夫·赫兹. 江苏理工学院 物理实验中心. [2013-11-20]. (原始内容存档于2015-06-10).
- ^ 心率计算与诊断. Etoolsage.com. [2013-11-22]. (原始内容存档于2021-05-15).
- ^ Bakshi, K.A.; A.V. Bakshi, U.A. Bakshi. Electronic Measurement Systems. US: Technical Publications. 2008: 4–14. ISBN 9788184312065. [失效链接]
- ^ 看到子彈正穿過撲克牌 快速攝影術的發明. 中华民国行政院国科会. [2013-11-20].[永久失效链接]
- ^ 光外差原理. 中山大学物理科学与工程技术学院. [2013-11-22].[永久失效链接]
- ^ 高一物理 机械波. 中基网. [2013-11-20]. (原始内容存档于2015-09-23).
- ^ 《科学》九年级(下). 中国: 华东师范大学出版社. ISBN 7-5617-3374-7.
- ^ Griffiths, David J., Hyperfine splitting in the ground state of hydrogen (PDF), American Journal of Physics, August 1982, 50 (8): pp. 698 [2010-11-23], (原始内容 (PDF)存档于2020-05-12)
- ^ 奈米〈Nanometer〉. 国立台湾大学科学教育发展中心. 2009-05-18 [2013-11-20]. (原始内容存档于2021-05-15).
- ^ Strain, George, How Well Do Dogs and Other Animals Hear?, [18 November 2010], (原始内容存档于2011-08-28)
- ^ Ausbreitung von Schall, [2021-12-12], (原始内容存档于2021-12-12)
- ^ Mietke, Detlef, Passive RC- und RL-Tiefpässe, [2021-12-12], (原始内容存档于2022-01-23)
- ^ 廖勇柏; 林宗毅,丁悌芬,李怡莹,黄琼瑶. 台灣地區行駛中火車車上電力頻磁場強度初探:以一個火車乘客為例. 劳工安全卫生研究季刊. 2006-06, 14 (2): 140–145.
- ^ 音響技術 (53). 1980.
- Giancoli, D.C. Physics for Scientists and Engineers 2nd. Prentice Hall. 1988. ISBN 013669201X.























