正扭歪無限面體

在幾何學中，正扭歪^[1]^[2]無限面體（英語：Regular skew apeirohedron），又稱扭歪正多面體（日語：ねじれ正多面体）^{[註 1]}是一種頂點並非全部共面的正無限面體，即每個面都全等、每個角也相等的扭歪無限面體。通常扭歪無限面體會具有正扭歪的面或扭歪的頂點圖。

歷史

關於考克斯特，1926年時，約翰·弗林德斯·皮特里將扭歪多邊形（非平面多邊形）的概念推廣到四維空間的扭歪多面體和三維空間的扭歪無限面體。

考克斯特找到了三種形式，他們具有平的面和扭歪的頂點圖，兩者彼此互補。它們都可以用施萊夫利符號的擴展符號{l,m|n}來表示。這個擴展符號{l,m|n}表示每個頂點都是 $m$ 個正 $l$ 邊形的公共頂點，且存在正 $n$ 邊形的空洞。

若一扭歪無限面體是一個正扭歪無限面體，則其施萊夫利符號存在下列等式：

2 sin( $π$ /l) · sin( $π$ /m) = cos( $π$ /n)

三維空間的正扭歪無限面體

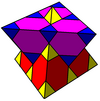
三維空間中有三種扭歪無限面體，分別為四角六片四角孔扭歪無限面體、六角四片四角孔扭歪無限面體和六角六片三角孔扭歪無限面體。約翰·康威將他們稱為多立方體（英語：Mucube）、多八面體（英語：Muoctahedron）和、多四面體（英語：Mutetrahedron），英文中的字首mu-表示「多」（英語：multiple）的意思，其意義分別代表「很多立方體」、「很多八面體」以及「很多四面體」^[3]。

四角六片四角孔扭歪無限面體（多立方體、英語：Mucube）：{4,6|4}：每個頂點都是六個正方形的公共頂點
六角四片四角孔扭歪無限面體（多八面體、英語：Muoctahedron）：{6,4|4}：每個頂點都是四個六邊形的公共頂點
六角六片三角孔扭歪無限面體（多四面體、英語：Mutetrahedron）：{6,6|3}：每個頂點都是六個六邊形的公共頂點

考克斯特給予這些 {2q,2r|p} 形式的扭歪無限面體與抽象群 (2q,2r|2,p) 同構的[[(p,q,p,r)]⁺的手徵對稱性。與之相關的堆砌就具有[[(p,q,p,r)]]的擴展對稱性^[4]。

緊空間正扭歪無限面體
考克斯特群對稱性	無限面體 {p,q\|l}	圖像	頂點圖	相關堆砌
[[4,3,4]] [[4,3,4]⁺]	{4,6\|4} 四角六片四角孔扭歪無限面體多立方體	動畫	扭歪六邊形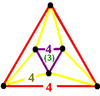（黃色部分）	t_0,3{4,3,4}
[[4,3,4]] [[4,3,4]⁺]	{6,4\|4} 六角四片四角孔扭歪無限面體多八面體	動畫	扭歪四邊形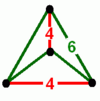（綠色部分）	2t{4,3,4}
[[3^[4]]] [[3^[4]]⁺]	{6,6\|3} 六角六片三角孔扭歪無限面體多四面體	動畫	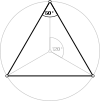扭歪六邊形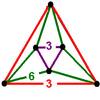（綠色部分）	q{4,3,4}（英語：Quarter cubic honeycomb）

三維雙曲空間的正扭歪無限面體

1967年時，C. W. L. Garner以類似於在歐式三維空間尋找正扭歪無限面體的方式，發現了31種雙曲空間中具有扭歪多邊形頂點圖的正扭歪無限面體^[5]。

14種緊空間正扭歪無限面體

14種緊空間正扭歪無限面體
考克斯特群	無限面體 {p,q\|l}	堆砌	無限面體 {p,q\|l}	堆砌
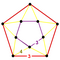
[3,5,3]	{10,4\|3}	2t{3,5,3}（英語：Bitruncated icosahedral honeycomb）	{4,10\|3}	t_0,3{3,5,3}（英語：Runcinated icosahedral honeycomb）
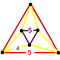
[5,3,5]	{6,4\|5}	2t{5,3,5}（英語：Bitruncated order-5 dodecahedral honeycomb）	{4,6\|5}	t_0,3{5,3,5}（英語：Runcinated order-5 dodecahedral honeycomb）
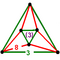
[(4,3,3,3)]	{8,6\|3}	ct{(4,3,3,3)}	{6,8\|3}	ct{(3,3,4,3)}
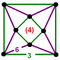
[(5,3,3,3)]	{10,6\|3}	ct{(5,3,3,3)}	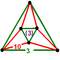{6,10\|3}	ct{(3,3,5,3)}
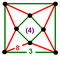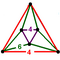
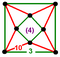
[(4,3,4,3)]	{8,8\|3}	ct{(4,3,4,3)}（英語：Cyclotruncated cubic-octahedral honeycomb）	{6,6\|4}	ct{(3,4,3,4)}（英語：Cyclotruncated octahedral-cubic honeycomb）
[(5,3,4,3)]	{8,10\|3}	ct{(4,3,5,3)}	{10,8\|3}	ct{(5,3,4,3)}
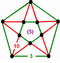
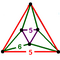
[(5,3,5,3)]	{10,10\|3}	ct{(5,3,5,3)}（英語：Cyclotruncated dodecahedral-icosahedral honeycomb）	{6,6\|5}	ct{(3,5,3,5)}（英語：Cyclotruncated icosahedral-dodecahedral honeycomb）

17種仿緊空間正扭歪無限面體

17種仿緊空間正扭歪無限面體
考克斯特群	無限面體 {p,q\|l}	堆砌	無限面體 {p,q\|l}	堆砌
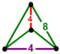
[4,4,4]	{8,4\|4}	2t{4,4,4}（英語：Bitruncated order-4 square tiling honeycomb）	{4,8\|4}	t_0,3{4,4,4}（英語：Runcinated order-4 square tiling honeycomb）
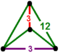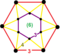
[3,6,3]	{12,4\|3}	2t{3,6,3}（英語：Bitruncated triangular tiling honeycomb）	{4,12\|3}	t_0,3{3,6,3}（英語：Runcinated triangular tiling honeycomb）
[6,3,6]	{6,4\|6}	2t{6,3,6}（英語：Bitruncated order-6 hexagonal tiling honeycomb）	{4,6\|6}	t_0,3{6,3,6}（英語：Runcinated order-6 hexagonal tiling honeycomb）
[(4,4,4,3)]	{8,6\|4}	ct{(4,4,3,4)}	{6,8\|4}	ct{(3,4,4,4)}
[(4,4,4,4)]	{8,8\|4}	q{4,4,4}（英語：Order-4 square tiling honeycomb）
[(6,3,3,3)]	{12,6\|3}	ct{(6,3,3,3)}	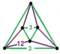{6,12\|3}	ct{(3,3,6,3)}
[(6,3,4,3)]	{12,8\|3}	ct{(6,3,4,3)}	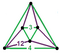{8,12\|3}	ct{(4,3,6,3)}
[(6,3,5,3)]	{12,10\|3}	ct{(6,3,5,3)}	{10,12\|3}	ct{(5,3,6,3)}
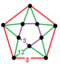
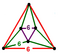
[(6,3,6,3)]	{12,12\|3}	ct{(6,3,6,3)}	{6,6\|6}	ct{(3,6,3,6)}

參見

註釋

^ 對於此主題（無限多個面的扭歪多面體），將之稱為「扭歪正多面體」可能會有歧義，因為非無限多面的扭歪多面體也可能是正多面體，例如正多面體#皮特里對偶。

參考文獻

^ 400年ぶりに新種の「対称性多面体」構造が発見される. gigazine.net. 2014-02-22 [2016-07-16]. （原始內容存檔於2020-11-19）.
^ 扭歪の意味. Weblio日中中日辭典. [2024-04-23]. （原始內容存檔於2013-07-20）.
^ The Symmetry of Things, 2008, Chapter 23 Objects with Primary Symmmetry, Infinite Platonic Polyhedra, pp. 333–335
^ Coxeter, Regular and Semi-Regular Polytopes II 2.34)
^ Garner, C. W. L. Regular Skew Polyhedra in Hyperbolic Three-Space. Canad. J. Math. 19, 1179–1186, 1967. [1] （頁面存檔備份，存於互聯網檔案館） Note: His paper says there are 32, but one is self-dual, leaving 31.

外部連結

埃里克·韋斯坦因. Regular Skew Polyhedron. MathWorld.

[3] 對於此主題（無限多個面的扭歪多面體），將之稱為「扭歪正多面體」可能會有歧義，因為非無限多面的扭歪多面體也可能是正多面體，例如正多面體#皮特里對偶。

[1] 400年ぶりに新種の「対称性多面体」構造が発見される. gigazine.net. 2014-02-22 [2016-07-16]. （原始內容存檔於2020-11-19）.

[2] 扭歪の意味. Weblio日中中日辭典. [2024-04-23]. （原始內容存檔於2013-07-20）.

[4] The Symmetry of Things, 2008, Chapter 23 Objects with Primary Symmmetry, Infinite Platonic Polyhedra, pp. 333–335

[5] Coxeter, Regular and Semi-Regular Polytopes II 2.34)

[6] Garner, C. W. L. Regular Skew Polyhedra in Hyperbolic Three-Space. Canad. J. Math. 19, 1179–1186, 1967. [1] （頁面存檔備份，存於互聯網檔案館） Note: His paper says there are 32, but one is self-dual, leaving 31.

[1]

[2]

[註 1]

[3]

[4]

[5]