 簡森不等式
簡森不等式
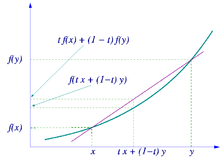
簡森不等式[1](英語:Jensen's inequality,中國大陸稱作琴生不等式),或稱延森不等式,以丹麥數學家約翰·延森命名。它給出積分的凸函數值和凸函數的積分值間的關係,在此不等式最簡單形式中,闡明了對一平均做凸函數轉換,會小於等於先做凸函數轉換再平均。若將簡森不等式應用在二點上,就回到了凸函數的基本性質:過一個凸函數上任意兩點所作割線一定在這兩點間的函數圖象的上方,即:

延森不等式可以用測度論或機率論的語言給出。這兩種方式都表明同一個很一般的結果。
假設 是集合
是集合 的正測度,使得
的正測度,使得 。若
。若 是勒貝格可積的實值函數,而
是勒貝格可積的實值函數,而 是在
是在 的值域上定義的凸函數,則
的值域上定義的凸函數,則

以機率論的名詞, 是個機率測度。函數
是個機率測度。函數 換作實值隨機變數
換作實值隨機變數 (就純數學而言,兩者沒有分別)。在
(就純數學而言,兩者沒有分別)。在 空間上,任何函數相對於機率測度
空間上,任何函數相對於機率測度 的積分就成了期望值。這不等式就說,若
的積分就成了期望值。這不等式就說,若 是任一凸函數,則
是任一凸函數,則

假設 是實數軸上的可測子集,而
是實數軸上的可測子集,而 是非負函數,使得
是非負函數,使得

以機率論的語言, 是個機率密度函數。
是個機率密度函數。
延森不等式變成以下關於凸積分的命題:
若 是任一實值可測函數,
是任一實值可測函數, 在
在 的值域中是凸函數,則
的值域中是凸函數,則

若 ,則這形式的不等式簡化成一個常用特例:
,則這形式的不等式簡化成一個常用特例:

若 是有限集合
是有限集合 ,而
,而 是
是 上的正規計數測度,則不等式的一般形式可以簡單地用和式表示:
上的正規計數測度,則不等式的一般形式可以簡單地用和式表示:

其中 。
。
若 是凹函數,只需把不等式符號調轉。
是凹函數,只需把不等式符號調轉。
假設 是正實數,
是正實數, ,
, 及
及 。上述和式便成了
。上述和式便成了

兩邊取取以 為底數的指數函數就得出熟悉的平均數不等式:
為底數的指數函數就得出熟悉的平均數不等式:
![{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef93c89e0de538cc0a557a6832bf287af496228a)
這不等式也有無限項的離散形式。
統計物理學中,若凸函數是指數函數,延森不等式特別重要:

其中方括號表示期望值,是以隨機變數X的某個機率分布算出。這個情形的證明很簡單(參見Chandler, Sec. 5.5):在以下等式的第三個指數函數

套用不等式

即得出所求的不等式。
- ^ Jensen's inequality - 簡森不等式. 國家教育研究院雙語詞彙. [2021-11-22]. (原始內容存檔於2021-11-22) (中文(臺灣)).

























![{\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef93c89e0de538cc0a557a6832bf287af496228a)


